Energy Conservation Principles
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Energy Conservation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to explore energy conservation in fluid mechanics. What can you tell me about the role of energy when fluids move from one place to another?

Energy helps in moving fluids and can be transformed, right?

Exactly! Energy can be transformed into work done by the fluid and heat transfer. Can anyone explain how heat transfer happens?

Heat transfers when there's a temperature difference.

Correct! This interaction is critical in understanding energy conservation. Remember, heat flow is like a game of hot and cold! The area between our system and surroundings plays a big role here.

So, energy conservation is important for fluid mechanics in many ways!

Yes! Let's emphasize that energy conservation principles connect to mass and momentum conservation as well.

Can you remind us of those principles?

Sure! Conservation of mass, linear momentum, and energy are the three fundamental principles we discuss. Remember: *M.E.M. - Mass, Energy, Momentum!*
Extensive and Intensive Properties
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's move on to the properties of fluids. What do you understand by extensive and intensive properties?

Extensive properties depend on the amount of substance, like mass and total energy.

Very well! And can someone give an example of an intensive property?

Specific energy is an intensive property because it doesn't depend on the total mass.

Exactly! Think: for every extensive property like total energy, we have an intensive counterpart like specific energy, which is energy per unit mass. Remember *E=E*m*!*

So if I have more mass, I have more total energy, but specific energy stays the same?

Spot on! This relationship is crucial for understanding fluid dynamics.
Reynolds Transport Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, we'll cover the Reynolds Transport Theorem. What is our primary goal with this theorem?

To relate system conservation laws to control volume analyses!

Excellent! Can anyone summarize what the Reynolds Transport Theorem provides?

It allows us to calculate the time rate of change of extensive properties in a control volume!

That's right! And remember that the mathematical representation can seem complex, but at its core, it's about linking how fluids behave within a defined control volume.

It feels a bit challenging. Can we break down the equation together?

Sure! Let's define the terms involved and how they relate to influx and outflux. Just keep in mind, *It’s all about flow, flux, and balance!*
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, the concepts of energy conservation in fluid systems are explored, emphasizing the importance of extensive and intensive properties. Additionally, the Reynolds transport theorem is introduced to relate system-level conservation laws to control volume analyses.
Detailed
Energy Conservation Principles
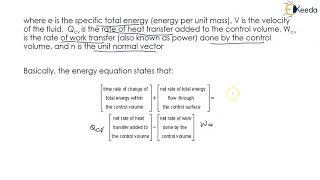
The conservation of energy is a fundamental principle in fluid mechanics, paralleling the conservation of mass and momentum. The section outlines how energy conservation is crucial when fluids move from one location to another, evaluating the work done by or against the fluid and interactions involving heat transfer due to temperature gradients.
Key Points:
- Conservation Principles: The three main conservation laws applicable in solid mechanics and fluid mechanics include:
- Conservation of mass
- Conservation of linear momentum (Newton’s laws)
- Conservation of energy (First law of thermodynamics)
- Extensive vs. Intensive Properties:
- Extensive properties depend on the mass of the system and include mass, momentum, and total energy. They increase with the amount of mass present.
- Intensive properties are independent of mass; examples include specific energy (energy per unit mass) and velocity.
- Reynolds Transport Theorem: This theorem establishes a relationship between conservation laws at the system level (closed mass) and control volume analysis (open mass), crucial for analyzing fluid behavior mathematically in various scenarios.
Conclusion:
Understanding these principles is vital for analyzing fluid systems and solving related engineering problems.
Youtube Videos








![[CFD] The Energy Equation for Solids and Fluids in CFD](https://img.youtube.com/vi/z8dZHze_EPo/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Energy Conservation in Fluids
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The conservation of momentum which is required for you to know it, how the fluid particles are moving it, what could be the force exerting on that, what could be the velocity. Similar way, we can understand the energy conservation which plays a major role for us when the fluid comes from one location to other locations, how much of work is done by the fluid or into the fluid.
Detailed Explanation
This chunk introduces the concept of energy conservation as it relates to fluids. It explains that as fluid particles move from one location to another, they exert forces and have velocities that are important to understanding energy conservation. The work done by the fluid, in terms of energy conservation, refers to the energy transfer that occurs as fluids interact with their surroundings or move through different states.
Examples & Analogies
Imagine a river flowing from a higher elevation to a lower one. As the water moves downstream, it has potential energy due to its height, which gets converted into kinetic energy as it speeds up. This exchange illustrates energy conservation in action, where the total energy remains constant but transforms as the fluid flows.
Key Energy Conservation Principles
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
To summarise this, that means, we all know that there are three energy conservation principles that we follow in solid mechanics when you consider as a system. Same concept also we can use at the system levels to solve the problems, conservation of mass, conservation of linear momentum which is Newton’s law, and the conservation of energy which is the first law of thermodynamics.
Detailed Explanation
This chunk summarizes the three fundamental principles of conservation relevant to fluid mechanics: conservation of mass, conservation of linear momentum, and conservation of energy. The conservation of mass states that mass cannot be created or destroyed; it must remain constant. The conservation of linear momentum relates to how a fluid maintains its motion unless acted upon by an external force, as described by Newton's laws. Lastly, the conservation of energy aligns with the First Law of Thermodynamics, which states that energy cannot be created or destroyed, only transformed.
Examples & Analogies
Think of energy conservation like a bicycle ride. When you pedal uphill, you use energy to change potential energy as you gain height, but as you ride downhill, that potential energy converts back into kinetic energy, and you speed up. Just like the bicycle, fluids maintain their energy and momentum as they flow, obeying these principles along their path.
Understanding Properties: Extensive vs. Intensive
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, let me define two types of properties that we have; one is called extensive property and the other is the intensive property. The extensive property which is considered as proportional to the amount of mass.
Detailed Explanation
In this section, the difference between extensive and intensive properties is clarified. Extensive properties depend on the amount of substance present; examples include mass, momentum, and energy. As the amount of mass increases or decreases, so do the extensive properties. Intensive properties, on the other hand, do not depend on the mass – they remain the same regardless of how much substance you have. Examples include temperature and pressure. For instance, while the energy of a system increases with added mass, the temperature (an intensive property) does not change.
Examples & Analogies
Consider a glass of water. If you fill it halfway, it has a certain temperature and mass. If you then fill it all the way, the temperature stays the same (intensive property), but the mass and total energy increase (extensive properties). This illustrates how extensive and intensive properties function differently in a real-world scenario.
Application of Reynolds Transport Theorem
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let us understand the Reynolds transport theorem which establish the relationship between the conservation law at the system level and the conservation at the control volume level.
Detailed Explanation
The Reynolds transport theorem is a critical concept that connects the conservation laws at the system level (the larger context of fluid mechanics) to those at the control volume level (specific areas within that system). It allows for the evaluation of changes in extensive properties over time, contributing to understanding how fluid properties evolve when considering a specific section of space or fluid (the control volume). This theorem is fundamental for deriving the equations governing mass, momentum, and energy in fluid systems.
Examples & Analogies
Think of the Reynolds transport theorem like tracking your morning coffee. If you consider yourself (the system) and your cup (the control volume), you can observe how the amount of coffee (mass) you pour in changes over time while also thinking about how the total amount of coffee in the pot (the system) remains constant unless something is added or taken out. This analogy helps in illustrating the dynamic changes in properties within a defined space.
Key Concepts
-
Conservation Principles: Three tools to analyze fluid systems are mass, momentum, and energy.
-
Extensive vs. Intensive Properties: Understanding how some properties depend on mass while others do not.
-
Reynolds Transport Theorem: It relates extensive properties and fluid flows, bridging the gap between system and control volume.
Examples & Applications
The total energy of a 10 kg mass is twice that of a 5 kg mass, illustrating the concept of extensive properties.
The specific energy of a fluid remains the same regardless of the volume of fluid, which showcases intensive properties.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Energy moves with ease, in fluid flows it aims to please.
Stories
Imagine a traveler carrying a backpack filled with water. The water represents total energy. As the traveler walks, this water symbolizes extensive properties they're bringing. But for every sip taken, they pour a little, representing intensive properties that remain consistent regardless.
Memory Tools
E=Em (Energy equals Energy times mass) to remember that energy total is based on mass.
Acronyms
M.E.M. - Mass, Energy, Momentum! To remember the conservation principles in fluid mechanics.
Flash Cards
Glossary
- Extensive Property
A property that depends on the amount of mass in the system (e.g., total energy, mass).
- Intensive Property
A property that is independent of mass (e.g., specific energy, velocity).
- Reynolds Transport Theorem
A theorem that relates the change in an extensive property within a system to the flux of that property across the control volume boundary.
- Heat Transfer
The movement of thermal energy between physical systems due to temperature differences.
Reference links
Supplementary resources to enhance your learning experience.
