Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Conservation Laws
Unlock Audio Lesson
Today, we'll dive into the core principles of fluid dynamics, specifically focusing on conservation laws. Can anyone tell me what conservation laws apply to fluids?
Isn't it conservation of mass, momentum, and energy?
Absolutely, great job! These three conservation laws play a crucial role in understanding fluid behavior. Remember the acronym MOM for Mass, Momentum, and Energy to recall these laws easily.
What does each conservation principle actually imply in fluid dynamics?
Good question! Conservation of mass implies that the mass of fluids remains constant in a closed system. For momentum, it means that the overall momentum changes only if an external force is applied. Energy conservation suggests that energy cannot be created or destroyed, only transformed. Now, let's see these principles in action!
Extensive vs. Intensive Properties
Unlock Audio Lesson
Next, we have extensive and intensive properties. Can someone explain the difference?
Extensive properties depend on mass, like total energy, while intensive properties do not, like temperature, right?
Exactly! A mnemonic to remember this is E for Extensive properties being 'extra' dependent on mass, while I for Intensive properties stands for 'Independent'.
Can you give examples of each?
Of course! Energy is an extensive property, while specific energy, which is energy per unit mass, is an intensive property. Understanding this distinction is crucial as we analyze fluid systems.
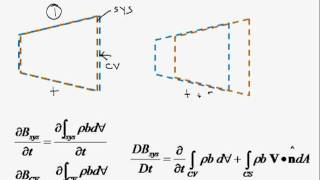
Reynolds Transport Theorem
Unlock Audio Lesson
Now, let’s move on to the Reynolds Transport Theorem. This theorem is essential for linking the system level and control volume level. How would you summarize its purpose?
It relates the change in a system’s property to the flow across its boundaries?
Exactly! It's the bridge between the two perspectives. To recall this, remember the phrase 'Flow into control'—it emphasizes the effects of flow across boundaries on system properties.
How do we derive it?
Good catch! We start by considering a control volume and the extensive properties within it at different times. Through careful analysis and integration, we establish RTT mathematically.
Application of RTT
Unlock Audio Lesson
Let’s discuss the application of RTT in fluid scenarios. How do we apply it?
I guess we need to analyze inflow and outflow from a control volume?
Exactly! By integrating the flux across the control surfaces, we can calculate mass, momentum, or energy transfers.
What tools do we use to perform these integrations?
We often employ calculus, using surface integrals to compute inflow and outflow. This application is vital in engineering calculations.
Summary of Key Concepts
Unlock Audio Lesson
As we wrap up, let’s summarize the key concepts. What are the main takeaways from today’s section?
The conservation principles in fluid dynamics: mass, momentum, and energy.
And the distinction between extensive and intensive properties!
Perfect! And of course, the importance of the Reynolds Transport Theorem for applications in fluid analysis. Remember, integration over control surfaces is essential!
Thanks, this was helpful!
Yes, I feel much more confident understanding these concepts now!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section introduces fundamental concepts in fluid mechanics such as conservation laws and differentiates between extensive and intensive properties. It emphasizes the Reynolds transport theorem, establishing the relationship between system-level and control-volume-level conservation laws, and describes the derivation and application of these principles in fluid dynamics.
Detailed
Integration Over Control Surfaces
This section focuses on the principles of conservation relevant in fluid mechanics, particularly the conservation of mass, momentum, and energy. These principles can be applied at the system level while also being represented through control volumes.
Key Concepts Covered:
- Conservation Laws: The three primary conservation laws discussed are conservation of mass, linear momentum (Newton’s law), and energy (the first law of thermodynamics). These laws are essential for analyzing fluid flows and are instrumental in the derivation of fluid behavior equations.
- Extensive vs. Intensive Properties: The section defines and differentiates between extensive properties, which are dependent on the amount of mass (e.g., total energy), and intensive properties, which are independent of mass (e.g., specific energy and velocity). This distinction is crucial in fluid analysis.
- Reynolds Transport Theorem (RTT): The main focus of the section is the derivation and implication of the Reynolds transport theorem, which relates the conservation laws at a system level to those at a control volume level. This theorem is pivotal in fluid mechanics, allowing for the calculation of changes in a system due to mass and energy flow across control surfaces.
- Application and Integration: Practical applications of analyzing inflow and outflow through control surfaces are discussed, including integrations over specific geometric configurations to compute mass, momentum, and energy fluxes.
The comprehension of these properties and forms is vital for students to analyze dynamic systems in fluid mechanics effectively.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Conservation Principles in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The conservation of momentum which is required for you to know it, how the fluid particles are moving it, what could be the force exerting on that, what could be the velocity. Similar way, we can understand the energy conservation which plays a major role for us when the fluid comes from one location to other locations, how much of work is done by the fluid or into the fluid. Similar way, whether there is heat transfers happening which you can feel it, if there is a temperature gradient there will be heat transfer either to the surrendering of the systems or into the systems or out of the system, that is what we can do.
Detailed Explanation
In fluid mechanics, understanding the conservation principles is crucial. These principles dictate how momentum and energy behave as fluid particles move within a system. Momentum conservation means that the total momentum of a fluid particle moving from one place to another is constant unless acted upon by an external force. On the other hand, energy conservation focuses on the work done by or on the fluid, highlighting how energy is transferred and transformed as fluid moves. Additionally, energy changes can also indicate heat transfers, which occur when there are temperature differences between the fluid and its surroundings.
Examples & Analogies
Think of a flowing river. As water moves from a higher elevation to a lower one, gravity exerts a force on it, conserving momentum as the current flows. The energy of the moving water can also do work, such as turning a water wheel or eroding riverbanks. The interaction with the surrounding environment, like heat exchanged with the air, can be understood through these conservation laws.
Extensive vs. Intensive Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let me define two types of properties that we have; one is called extensive property and the other is the intensive property. The extensive property which is considered as proportional to the amount of mass. Extensive properties are proportional to the amount of mass, meaning, as mass increases, the extensive properties increase, and vice versa. When looking at intensive properties, they are independent of mass.
Detailed Explanation
Extensive properties depend on the amount of substance present in a system. For instance, mass, momentum, and energy are extensive properties because they increase when more substance is added. In contrast, intensive properties do not change regardless of the amount of substance. Examples include temperature and density, which remain consistent even if the mass of the substance increases. This distinction is crucial in fluid mechanics as it helps in analyzing different properties of fluids under various conditions.
Examples & Analogies
Imagine a glass of milk. If you have half a glass, the temperature of that milk remains the same whether it’s a full glass or half. Temperature is an intensive property. However, if you pour in more milk, the total mass increases, which affects the extensive property of the milk’s volume.
Reynolds Transport Theorem Introduction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, we will go to derive Reynolds transport theorem. The derivation of the Reynolds transport theorem is available in almost all the fluid mechanics books. The idea for me is to introduce the Reynolds transport theorem so that you can easily understand it.
Detailed Explanation
The Reynolds transport theorem provides a framework for relating the behavior of a fluid system as a whole (system level) with a specific control volume that moves or deforms over time. It combines the principles of mass, momentum, and energy conservation with the changes that occur within a control volume. This theorem helps us analyze how fluid properties change as they flow in and out of defined boundaries, making it a fundamental concept in fluid mechanics.
Examples & Analogies
Consider a bathtub where water is flowing in through the tap and out through the drain. The Reynolds transport theorem can be used to analyze changes in water level within the tub over time. It highlights how the amount of water in the tub (control volume) relates to the inflow and outflow at a system level.
Deriving the Theorem with Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
First, what we are considering is a non-deforming control volume which I have drawn the streamlines representing the flow that is coming in and coming out. That is what is my control volume. Whatever the fluid particles present at time t will represent the control volume and the reason is these are fixed.
Detailed Explanation
In deriving the Reynolds transport theorem, we start with a control volume that does not change shape (non-deforming). This control volume is like a designated area in space through which fluid flows. We define the boundaries of this area and examine how fluid properties are distributed and change over time. By analyzing how fluid enters and exits this space, we can formulate equations that describe the dynamics of the fluid and its properties.
Examples & Analogies
Think about a water cup that has been marked with a line to indicate a fixed volume. The cup represents your control volume. You can observe water entering the cup from a faucet and leaving through a straw. By monitoring the amount of water that flows in and out, you can apply the concepts of the Reynolds transport theorem to analyze changes in water level.
Analyzing Influx and Outflux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if I look at simple definitions, the calculus is that the time rate of change of B in the system as a definition t + dt minus the system at the t level. We are defining in terms of in or out.
Detailed Explanation
When analyzing how fluid moves through a control volume, we need to account for both the fluid that enters the system (influx) and the fluid that exits (outflux). By observing the changes in these flows over a specific time period (from time t to t + dt), we can use calculus to quantify these rates of change. This involves looking at the difference in the property B between these two time points and integrating this across the control surface.
Examples & Analogies
Consider a water tank being filled and drained. If you monitor how much water comes in through the inlet pipe and how much leaves through the outlet pipe in a minute, you can assess whether the tank is gaining, losing, or holding a constant volume of water. This concept of influx and outflux is crucial in determining the dynamics of the water level.
Total Change in Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I know the velocity and the unit vectors, if I know the b and if I know the density, how it varies, then we can find out what could be the net outflux that is coming out if we are doing surface integrals of these functions.
Detailed Explanation
To compute the total change in property B within a control volume over time, we need to gather data on the velocity of the fluid, the density of the fluid, and a variety of other factors. By performing surface integrals over the control surface, we can calculate the net outflux or influx of fluid and how these factors influence the overall behavior of the system. This requires integrating across the entire surface area affected by the fluid flow.
Examples & Analogies
Imagine a water hose attached to a sprinkler system. By measuring the speed of water coming out of the hose and the area of the sprinkler head, you can calculate how much water flows through in a given period. This involves understanding both the flow rate and the area of the exit points to comprehend how much water is applied to your yard.
Applying the Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, coming to the third part. The first two terms we can write it as earlier you will have the influx and outflux. If you combine these, you get the total change in B at the control volume level.
Detailed Explanation
After establishing the influx and outflux components in the previous steps, we can combine these terms to express the total change of property B within our control volume. This is a critical step in applying the Reynolds transport theorem, as it allows us to relate how much of property B is accumulated in the control volume compared to what flows in and out. The theorem ultimately helps us create a comprehensive understanding of the behavior of fluid flows and their effects.
Examples & Analogies
Think about a swimming pool that is being filled. If you monitor how much water comes in from the hose but also how much escapes through leaks, you can calculate the effective increase or decrease in the water level over time. This cumulative understanding of influx versus outflux is at the heart of managing water in the pool efficiently.
Summary of the Chapter
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
With these things let me summarise today’s lecture. We discussed about system and control volume. We talked about fixed and deformable and moving control volume concept. The more important thing is that we derived the Reynolds transport theorem which can be used for fixed control volume, deformable control volume, moving control volume.
Detailed Explanation
The key points covered in this section include the importance of understanding systems and control volumes, the differences between fixed and deforming control volumes, and the derivation of the Reynolds transport theorem. This theorem is fundamental for analyzing fluid flow dynamics across various types of control volumes and forms the basis for many applications within fluid mechanics.
Examples & Analogies
In summary, think of the principles discussed as tools in a toolbox for engineers. The understanding of control volumes and conservation laws provides them with the ability to tackle complex fluid behavior in real-world scenarios, much like knowing how to use specific tools for carpentry helps build a solid structure.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Conservation Laws: The three primary conservation laws discussed are conservation of mass, linear momentum (Newton’s law), and energy (the first law of thermodynamics). These laws are essential for analyzing fluid flows and are instrumental in the derivation of fluid behavior equations.
-
Extensive vs. Intensive Properties: The section defines and differentiates between extensive properties, which are dependent on the amount of mass (e.g., total energy), and intensive properties, which are independent of mass (e.g., specific energy and velocity). This distinction is crucial in fluid analysis.
-
Reynolds Transport Theorem (RTT): The main focus of the section is the derivation and implication of the Reynolds transport theorem, which relates the conservation laws at a system level to those at a control volume level. This theorem is pivotal in fluid mechanics, allowing for the calculation of changes in a system due to mass and energy flow across control surfaces.
-
Application and Integration: Practical applications of analyzing inflow and outflow through control surfaces are discussed, including integrations over specific geometric configurations to compute mass, momentum, and energy fluxes.
-
The comprehension of these properties and forms is vital for students to analyze dynamic systems in fluid mechanics effectively.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of conservation of mass can be seen in water flowing through a pipe.
-
In a closed tank, the total energy remains constant, illustrating the conservation of energy.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
MOM keeps the flow, fluids in tow, Mass, Momentum, Energy - the trio we know!
📖 Fascinating Stories
-
Imagine a river (mass) flowing down a mountain (momentum) and the energy from its flow creating electricity (energy). Together, they keep the environment balanced.
🧠 Other Memory Gems
-
E for Extensive because it’s Exaggerated based on mass, I for Intensive meaning Independent, like temperature or pressure!
🎯 Super Acronyms
REM
- Reynolds
- Energy
- Mass - remember this for fluid conservation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Conservation of Mass
Definition:
A principle stating that the mass of an isolated system remains constant, regardless of changes in the system.
-
Term: Conservation of Momentum
Definition:
The principle that the total momentum of a closed system does not change unless acted upon by an external force.
-
Term: Conservation of Energy
Definition:
A principle asserting that energy cannot be created or destroyed, only transformed from one form to another.
-
Term: Extensive Properties
Definition:
Properties that depend on the amount of mass present in a system, such as total mass or total energy.
-
Term: Intensive Properties
Definition:
Properties that do not depend on the amount of mass, such as temperature or pressure.
-
Term: Reynolds Transport Theorem (RTT)
Definition:
A theorem that relates the time rate change of a property for a system to that of a control volume by accounting for the flow across the control surface.
-
Term: Control Volume
Definition:
A specified volume in fluid mechanics used to analyze the behavior of fluids within given boundaries.