Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Conservation Principles
Unlock Audio Lesson
Today we are diving into some key principles in fluid dynamics. Can anyone tell me what the conservation of mass means in fluid mechanics?
It means that mass cannot be created or destroyed in a closed system.
Exactly! Now, how about the conservation of momentum? Who can explain that?
It's about the amount of motion in a system being constant unless acted on by an external force.
Perfect! Let’s remember that with the acronym 'MOM' for Mass, Outflux, and Momentum. And what can you tell me about the conservation of energy?
Energy can't be created or destroyed, only transformed from one form to another.
Great job! This brings us to our next point: how do these principles relate to control volumes. Remember: Mass, Outflux, Momentum - MOM!
Extensive vs. Intensive Properties
Unlock Audio Lesson
Now let’s discuss extensive and intensive properties. Who can define what an extensive property is?
Extensive properties depend on the amount of mass present.
Correct! Can you give me some examples?
Mass, momentum, and energy are all examples of extensive properties.
Very well! Now, what about intensive properties?
They are independent of mass, like temperature or pressure.
Right! Let's make a mnemonic to remember: 'IE' for Intensive Equals independent. Now, with this framework, how do we use these properties in relation to control volumes?
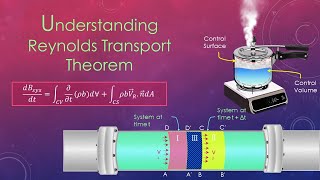
Reynolds Transport Theorem
Unlock Audio Lesson
Now, let’s shift gears to the Reynolds transport theorem, or RTT. This theorem connects system and control volume analyses. Can any of you summarize its significance?
It shows how changes in a system relate to changes in a control volume through flux.
Exactly! It outlines the relationship between the time rate of change of an extensive property in a system and the net flux into that control volume. Which equations represent this concept?
The equation shows that the time rate of change equals the accumulation plus the net outflux.
Correct! Let's remember it with the acronym 'ACORN': Accumulation + Control Volume = Outflux Rate + Net Change. Keep that in mind!
Flux Calculation
Unlock Audio Lesson
Next, let’s talk about calculating flux through our control surfaces. What factors influence this calculation?
The area of the surface and the velocity of the fluid.
Correct! And how do we express this mathematically?
We can use the dot product of the velocity vector and the area vector.
Exactly! Always remember: 'Area and Velocity, the duo of flow.' Now, how do we apply this in real-world scenarios?
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains how the concepts of extensive and intensive properties influence the conservation of mass, momentum, and energy within a control volume. It elaborates on the Reynolds transport theorem and its significance, offering insights into how these principles apply to fluid mechanics.
Detailed
Detailed Summary
In this section, we explore the fundamental principles governing fluid mechanics, specifically examining the conservation of mass, momentum, and energy. The concepts of extensive and intensive properties are crucial in understanding these principles. Extensive properties, which depend on mass, include mass, momentum, and energy, while intensive properties are independent of mass, such as velocity and specific energy.
The section introduces the Reynolds transport theorem (RTT), a pivotal concept connecting system-level conservation laws to control volume applications. RTT allows for analyzing how properties change in a control volume as fluids move through it.
We define a control volume, explaining how to evaluate changes during time intervals, and differentiate between inflow and outflow through a control surface. The mathematics of these principles are laid out, with a clear connection between accumulated mass or energy and the flux across the control surface. The concept of non-deforming control volumes is discussed to illustrate how to compute influx and outflux effectively, ultimately applying these principles to derive critical conservation equations in fluid mechanics.
Youtube Videos
![System Approach and Control Volume Approach [Fluid Mechanics]](https://img.youtube.com/vi/quK9rvsZTPA/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Conservation Principles in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The conservation of momentum which is required for you to know it, how the fluid particles are moving it, what could be the force exerting on that, what could be the velocity. Similar way, we can understand the energy conservation which plays a major role for us when the fluid comes from one location to other locations, how much of work is done by the fluid or into the fluid.
Detailed Explanation
In fluid mechanics, we can understand two key principles: the conservation of momentum and the conservation of energy. Conservation of momentum deals with how the motion of fluid particles is affected by the forces acting on them. It tells us that the momentum of a fluid system will be constant unless acted upon by external forces. Similarly, the conservation of energy states that as fluid moves from one place to another, it can do work on its surroundings or gain work itself due to the energy transferred within the fluid.
Examples & Analogies
Think of momentum conservation like a game of pool. When the cue ball hits another ball, it transfers momentum to that ball, causing it to move. Without any obstacles (like frictional forces), the total momentum before and after the hit remains the same. In energy conservation, imagine a water slide; as the water flows down, it loses potential energy but gains kinetic energy, illustrating how energy moves from one form to another.
Extensive vs. Intensive Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let me define two types of properties that we have; one is called extensive property and the other is the intensive property. The extensive property which is considered as proportional to the amount of mass. When you apply extensive properties, that means you are the properties which are proportional to the amount of mass.
Detailed Explanation
Extensive properties are dependent on the amount of substance present. This means that if you have a larger quantity of a fluid, its extensive properties, like mass, momentum, and energy, will also increase. For instance, the total mass of water in a tank is the sum of the water in it; if you add more water, the total mass increases. On the other hand, intensive properties are independent of the amount of substance. They remain constant regardless of how much of the fluid you have. Examples include temperature and pressure.
Examples & Analogies
Imagine a pure gold necklace. Its value (an extensive property) increases with its weight; more gold means a higher value. However, the purity of the gold (an intensive property) remains the same no matter how much you have. This concept applies to fluids where temperature or pressure does not change even if the volume of fluid changes.
Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, to summarise this, that means, we all know that there are three energy conservation principles that we follow in solid mechanics when you consider as a system. Same concept also we can use at the system levels to solve the problems, conservation of mass, conservation of linear momentum which is Newton’s law, and the conservation of energy which is the first law of thermodynamics. As I discussed, there is a system and control volume.
Detailed Explanation
Reynolds Transport Theorem (RTT) provides a linkage between the behavior of fluids in a system (fixed mass) and within a control volume (open mass). It allows us to calculate how properties like mass or energy change over time, connecting the accumulation of these properties within the control volume to their inflow and outflow across the control surface. The theorem essentially states that the rate of change of a property within a fixed system equals the change in the property within a control volume plus the net flux out of the control volume.
Examples & Analogies
Consider a bathtub. If you fill it with water while simultaneously draining some out, RTT allows you to account for how much water is in the tub at any moment. The water that flows in adds to the total, and the water that drains out reduces it, which helps us understand how much water is accumulating in the tub over time.
Deriving the Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let us come to the derivations which I will highlight as I say it while derivation, which are the major components, not line by line. So, first, what we are considering is a non-deforming control volume...
Detailed Explanation
To derive the Reynolds Transport Theorem, we first define our non-deforming control volume and observe how the fluid enters and exits through its surface. We analyze how the extensive properties like mass, momentum, and energy are distributed and how they change over time within this control volume. By applying the principle of conservation for each property, we formulate the mathematical relationships needed to express the changes of these properties within the control volume in terms of influx and outflux.
Examples & Analogies
Think of a classroom where students enter and leave. The total number of students at any time can change based on who walks in and out. When we derive RTT, we're essentially computing how the number of students changes over time based on those entering (influx) and those leaving (outflux), just like we compute changes in fluid properties.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Conservation Principles: The laws that govern the behavior of mass, momentum, and energy in a closed system.
-
Extensive vs Intensive Properties: Extensive properties depend on the amount of mass, while intensive properties do not.
-
Reynolds Transport Theorem: A key theorem relating the conservation laws in system and control volume contexts.
-
Flux: The quantitative measure of how much of a property flows through a unit area.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When analyzing a pipe flow, conservation of mass indicates that mass entering the pipe must equal mass exiting.
-
In analyzing energy flow in a heat exchanger, extensive properties like total energy must be accounted for while intensive properties like temperature remain uniform.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluids we flow, mean mass will stay, conservation of rules, keeps loss away.
📖 Fascinating Stories
-
Imagine a sealed jar of jellybeans. No matter how many you take out, the total weight always matches what’s put back, since beans can’t just vanish!
🧠 Other Memory Gems
-
MOM - Mass, Outflux, Momentum.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Conservation of Mass
Definition:
The principle that mass cannot be created or destroyed in an isolated system.
-
Term: Extensive Property
Definition:
A property that is dependent on the quantity of matter in the system.
-
Term: Intensive Property
Definition:
A property that does not depend on the amount of substance present.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that provides a relationship between the rates of change of a property in a control volume and a system.
-
Term: Flux
Definition:
The rate of flow of a property per unit area.