Overview of Energy Conservation in Solid Mechanics
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Energy Conservation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome class! Today, we will discuss energy conservation in solid mechanics. Can anyone tell me what energy conservation means in this context?

Does it mean keeping track of the energy we use when fluids move?

Exactly! Energy conservation in solid mechanics relates to how energy is managed when fluids move from one place to another, including work done by the fluid. Great job!

What about heat transfer? Is that part of energy conservation too?

Yes! Heat transfer plays a crucial role, especially when temperature gradients exist. This means energy can either flow into or out of a system.

So, what are the main conservation laws we should remember?

We focus on three main laws: mass conservation, momentum conservation, and energy conservation as per the first law of thermodynamics.

That’s a lot to remember. Any tips for keeping them straight?

A great way to remember is the acronym 'M.E.M.', standing for Mass, Energy, and Momentum. Let's dive deeper into each principle.

In summary, energy conservation ensures that when fluids are in motion, we consider both the work done and heat transfer affecting a system.
Extensive vs. Intensive Properties
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s differentiate between extensive and intensive properties. Who can summarize the difference?

Extensive properties depend on the amount of mass, while intensive properties don’t, right?

Correct! Extensive properties include things like mass and total energy, which grow as mass increases. Can anyone give an example of an intensive property?

Specific energy comes to mind since it's energy per unit mass.

Yes! Specific energy is a perfect example of an intensive property. Remember, for energy conservation, extensive properties help calculate the total energy in a system, while intensive properties can help describe the state of the system regardless of mass.

How do we apply these properties in equations?

Great question! We apply extensive properties when we refer to the total mass, while intensive properties are essential when considering per-unit calculations, such as flow rates.

In summary, understanding these properties is key to formulating conservation equations accurately.
Reynolds Transport Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's delve into the Reynolds transport theorem. What do you think it does?

Does it connect conservation laws at the system and control volume level?

Spot on! The theorem is foundational in linking changes observed in a system with those in a control volume. Who can explain the basic idea behind it?

I think it's about how to account for the net influx and outflux balance over time.

Exactly right! The equation tells us how the change in a property within a system relates to the net flux through the control surface over time.

Are there steps we follow to derive this theorem?

Yes! We consider time increments and balance the quantities flowing in and out. We'll work on this derivation more as we continue. For now, remember that the theorem is crucial for fluid mechanics.

In summary, Reynolds transport theorem provides a structured link between system dynamics and control volume analysis.
Applications of Energy Conservation in Problems
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let's explore how we use these principles in practical problems. Has anyone encountered a scenario where energy conservation matters in solid mechanics?

I remember something about calculating flow rates in pipes.

That's a perfect application! We can calculate flow based on energy conservation. What concepts might we apply here?

We could use both extensive and intensive properties for uniform flow rates.

Definitely! Remember, we often simplify conditions like assuming steady-state flow to make calculations easier.

How do we approach these calculations systematically?

Begin by defining your control volume and apply the Reynolds transport theorem to derive the necessary equations. Each principle will guide the process.

In summary, applying energy conservation principles allows us to tackle fluid mechanics problems efficiently!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section provides an overview of energy conservation in solid mechanics, detailing the connection between momentum, mass, and energy, and introduces the Reynolds transport theorem as a means to link system-level and control volume dynamics. It distinguishes between extensive and intensive properties crucial for understanding fluid behaviors in mechanics.
Detailed
Overview of Energy Conservation in Solid Mechanics
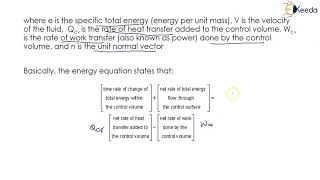
This section focuses on the critical principles of energy conservation in the context of solid mechanics. The conservation of momentum is essential for understanding fluid dynamics, as it encompasses how fluids move and the forces that act on them. Two major forms of energy transfer are noted: work done by fluids moving between locations and heat transfer influenced by temperature gradients. The section emphasizes three primary conservation laws in solid mechanics: mass conservation, linear momentum conservation, and energy conservation as dictated by the first law of thermodynamics. It then introduces the Reynolds Transport Theorem, which illustrates the relationship between these conservation laws at the system level and control volume level.
Extensive vs. Intensive Properties
The section also defines extensive properties (which depend on mass, e.g., mass and energy) and intensive properties (which are independent of mass, e.g., specific energy and velocity). These distinctions are crucial for applying conservation principles effectively. The discussion on Reynolds transport theorem derivation sets the foundation for understanding fluid mechanics' more complex dynamics, especially in non-deforming control volumes, allowing for clear definitions of influx and outflux contributing to conservation equations. In the following lectures, the importance of these principles and their applications in solving fluid mechanics problems will be further analyzed.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Energy Conservation
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The conservation of momentum which is required for you to know it, how the fluid particles are moving it, what could be the force exerting on that, what could be the velocity. Similar way, we can understand the energy conservation which plays a major role for us when the fluid comes from one location to other locations, how much of work is done by the fluid or into the fluid.
Detailed Explanation
This chunk introduces the concept of energy conservation in solid mechanics. It highlights the importance of understanding not just how momentum is conserved (which is about movement of objects and the forces acting on them) but also how energy conservation is crucial in analyzing fluid behavior. When fluid moves from one location to another, work is done, which is a core aspect of energy conservation.
Examples & Analogies
Think of riding a bicycle down a hill. As you descend, your potential energy (related to your height) converts into kinetic energy (related to your speed). Here, energy conservation means that the total amount of energy remains constant as it transfers from one form to another. Similarly, fluids moving through a pipe can lose pressure energy while gaining kinetic energy.
Heat Transfers and Temperature Gradient
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Similar way, whether there is heat transfers happening which you can feel it, if there is a temperature gradient there will be heat transfer either to the surrendering of the systems or into the systems or out of the system, that is what we can do.
Detailed Explanation
In this section, the text explains that heat transfer occurs due to temperature differences. When there is a temperature gradient (difference), heat will flow from the hotter region to the cooler region, and this can influence the overall energy conservation in a system.
Examples & Analogies
Consider a hot cup of coffee placed in a cooler room. Over time, the coffee cools down as heat transfers to the surrounding air. This illustrates energy conservation as energy leaves the coffee (hotter) system to reach the room (cooler), showing how thermal energy behaves.
Three Principles of Energy Conservation
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
To summarise this, that means, we all know that there are three energy conservation principles that we follow in solid mechanics when you consider as a system: conservation of mass, conservation of linear momentum which is Newton’s law, and the conservation of energy which is the first law of thermodynamics.
Detailed Explanation
Here, the text summarizes the three key principles that guide our understanding of energy in solid mechanics: conservation of mass states that mass cannot be created or destroyed, momentum conservation relates to Newton's laws of motion, and energy conservation aligns with the first law of thermodynamics, which states that energy cannot be created or destroyed but only transformed.
Examples & Analogies
Imagine a closed balloon filled with air. The air (mass) stays constant unless the balloon is popped (mass loss). When you squeeze the balloon (momentum), the air inside shifts but the total mass is unchanged. And as you release it, the air pushes back out, reflecting the conservation of energy as energy is transformed into motion.
Extensive and Intensive Properties
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, let me define two types of properties that we have; one is called extensive property and the other is the intensive property. The extensive property which is considered as proportional to the amount of mass.
Detailed Explanation
This chunk introduces two key concepts in thermodynamics: extensive and intensive properties. Extensive properties are dependent on the amount of matter in a system (e.g., mass and volume), while intensive properties exist independently of the quantity of matter (e.g., temperature and pressure). Understanding these properties helps distinguish how different variables affect energy conservation.
Examples & Analogies
Imagine a pizza. If you have one whole pizza, the amount of cheese (extensive property) depends on how big the pizza is. But if you take a slice, the temperature of the cheese (intensive property) stays the same regardless of how much cheese is left in the entire pizza.
Reynolds Transport Theorem Overview
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, we will go to derive Reynolds transport theorem. The derivation of the Reynolds transport theorem are available in almost all the fluid mechanics books.
Detailed Explanation
The Reynolds Transport Theorem is a fundamental principle in fluid mechanics that connects the change in properties (like mass, momentum, and energy) in a system to those in a control volume that contains the system. It provides a mathematical framework needed to analyze fluid flow and conservation laws in various contexts.
Examples & Analogies
Think of a river flowing through a region. The properties of the water (like speed and volume) at one point in the river can change over time. The Reynolds transport theorem would help us understand how these changes relate to the entire volume of water (control volume) flowing past that point, much like gauging how much water passes a particular spot in a given time period.
Key Concepts
-
Energy Conservation: It's the principle that energy in a closed system remains constant.
-
Extensive and Intensive Properties: Understanding these properties helps in analyzing fluid behaviors effectively.
-
Reynolds Transport Theorem: A key theorem that connects the analysis of properties at the system level and control volume level.
Examples & Applications
Calculating flow rates in a pipeline using energy conservation principles, accounting for both the influx and outflux.
Analysis of temperature changes in a system due to heat transfer and its impact on energy conservation.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Energy in flow, here we know, can never die; it just moves high and low.
Stories
Imagine a river flowing through a valley. As the water moves, it carries energy from one place to another, never increasing or decreasing, just changing its form, like energy in our lives.
Memory Tools
M.E.M. - Mass, Energy, Momentum - the three key principles in solid mechanics.
Acronyms
E.C.M. - Energy Conservation Mechanisms help us remember the core ideas of energy flow.
Flash Cards
Glossary
- Energy Conservation
A principle stating that energy cannot be created or destroyed, only transformed from one form to another.
- Extensive Property
A property that depends on the amount of mass in a system, such as total mass or energy.
- Intensive Property
A property that does not depend on the amount of mass, such as density or specific energy.
- Reynolds Transport Theorem
A theorem that relates the change of a property in a control volume to the flux of that property across the control surface.
- Control Volume
A defined region in space through which fluid flows, used for analyzing fluid motion and energy transfer.
Reference links
Supplementary resources to enhance your learning experience.
