Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Control Volume Analysis
Unlock Audio Lesson
Today, we're diving into control volume analysis, which is fundamental in fluid mechanics. What are some of the main conservation laws we should keep in mind?
I think conservation of mass is one of them.
Exactly! Conservation of mass states that mass cannot be created or destroyed. What else?
Conservation of momentum, right?
Correct! This one is derived from Newton's laws. And, what about energy?
That's the first law of thermodynamics.
Good! All three are critical for control volume analysis. Remember the acronym 'MEM' for Mass, Energy, and Momentum!
MEM, got it!
Great! So, to summarize: control volume analysis utilizes these conservation laws to evaluate fluid behaviors and changes.
Properties of Fluids: Extensive vs. Intensive
Unlock Audio Lesson
Let’s explore properties of fluids now. Can anyone define extensive properties?
Those are properties that depend on the amount of fluid present, like mass or energy.
Perfect! And what about intensive properties?
They don't depend on how much fluid you have, like temperature or pressure.
Exactly! Remember: extensive properties are like 'Xtra' things you measure when you have more mass. What's an example of both?
Energy is extensive, while density is intensive!
Awesome—let's keep in mind how these properties play into analyzing control volumes and the Reynolds transport theorem.
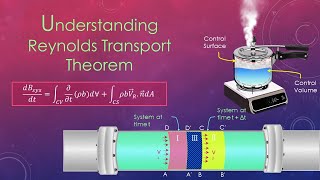
Reynolds Transport Theorem
Unlock Audio Lesson
Now we’re getting into the Reynolds transport theorem. Can anyone explain its relevance?
It connects system level behavior to control volume changes, right?
Exactly! It's crucial for understanding how fluid properties change over time within a control volume. Can anyone tell me how it relates to the conservation laws?
The theorem essentially says that the time rate of change in a system equals the rates of change within a control volume plus the net flow across its boundaries?
Spot on! Remember the phrase: 'In vs. Out' — that's how we balance these properties.
So, we can calculate changes over time as fluids flow in and out?
Yes, and that's a key application! Keep that 'In vs. Out' concept in mind as we apply this theorem to practical problems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Control volume analysis revolves around key conservation laws—mass, momentum, and energy. It explores the distinction between extensive and intensive properties, leading to the derivation of the Reynolds transport theorem, establishing their connection between system levels and control volumes.
Detailed
Understanding Control Volume Analysis
This section delves into the principles of control volume analysis, crucial for understanding fluid mechanics and thermodynamics. At its core lies the conservation of momentum, mass, and energy. These principles allow for a comprehensive analysis of how fluids behave in various systems. To understand these principles, we first differentiate between two types of properties:
Extensive vs. Intensive Properties
- Extensive Properties: These are proportional to mass, such as mass itself, momentum, and energy. If mass increases, these properties will also increase.
- Intensive Properties: These are mass-independent, such as density and specific energy. They reflect characteristics of the fluid irrespective of the quantity present.
Reynolds Transport Theorem (RTT)
The RTT provides the foundation for analyzing fluid flow through control volumes. It relates system-level conservation laws to control volume analysis. The derivation, which spans across basic calculus and physics principles, connects influx and outflux of fluid to changes within a control volume. As fluids enter or exit a designated control area, RTT allows the calculation of changes in extensive properties over time, directly linking them to net flow across the control surface.
Applications
The application of RTT is extensive and vital for deriving equations governing fluid dynamics (mass, momentum, and energy equations). For example, in steady incompressible flow, where density remains constant, the simplifications derived from RTT make calculations more manageable.
Through this section, students are guided to not only understand these principles theoretically but also see their practical utility in solving fluid dynamics problems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Principles of Conservation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The conservation of momentum which is required for you to know it, how the fluid particles are moving it, what could be the force exerting on that, what could be the velocity. Similar way, we can understand the energy conservation which plays a major role for us when the fluid comes from one location to other locations, how much of work is done by the fluid or into the fluid.
Detailed Explanation
This chunk introduces the core principles of fluid mechanics related to conservation laws. It emphasizes the conservation of momentum, which focuses on how fluid particles move, the forces acting on them, and their velocities. It also mentions the conservation of energy, illustrating how energy is transferred when fluids move between locations and do work.
Examples & Analogies
Think of a flowing river. The momentum conservation principle can be related to how fast the water flows (velocity) and the rocks or banks (forces) that might slow it down. Energy conservation can be seen when the water does work by turning a watermill as it flows, transferring its energy to the mill.
Types of Properties: Extensive vs. Intensive
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let me define two types of properties that we have; one is called extensive property and the other is the intensive property. The extensive property which is considered as proportional to the amount of mass. When you apply extensive properties, that means you are the properties which are proportional to the amount of mass. That means, as mass increases you will have extensive properties going to increase.
Detailed Explanation
This chunk defines two fundamental types of properties in fluid mechanics: extensive properties and intensive properties. Extensive properties depend on the mass of the system (e.g., total mass, total energy), meaning that if you increase the mass, these properties will increase respectively. In contrast, intensive properties are independent of the mass (e.g., temperature, pressure) and remain constant regardless of the system's size.
Examples & Analogies
Imagine a pizza: its size (extensive property) depends on how many slices you order. If you order two pizzas, the total area increases. However, the temperature of the pizza (intensive property) remains the same whether you have one slice or an entire pie.
Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, we will go to derive Reynolds transport theorem. The derivation of the Reynolds transport theorem are available in almost all the fluid mechanics books. The idea for me is to introduce the Reynolds transport theorem so that you can easily understand it.
Detailed Explanation
This chunk introduces the Reynolds Transport Theorem (RTT), which establishes a relationship between the changes in a system (like a set of fluid particles) and a control volume. The theorem allows us to analyze how properties change over time in a fluid system, facilitating the analysis of mass, momentum, and energy within that volume.
Examples & Analogies
Consider a sponge filled with water. If you squeeze it, some water (mass) escapes, and your hand applies pressure (force). The quantity of water released can be analyzed using the RTT, helping you understand how much fluid is lost (change in properties) from your original sponge (system) during the squeezing (control volume analysis).
Control Volume Descriptions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, first, what we are considering is a non-deforming control volume. And this is my non-deformable control volume and also I have drawn the streamlines representing the flow that is coming in and coming out.
Detailed Explanation
This chunk explains the concept of a control volume, emphasizing non-deforming or fixed bodies of fluid over time, within which we analyze the flow of the fluid. It mentions streamlines to visualize the direction of fluid movement into and out of the control volume, which helps in understanding fluid behavior and interactions at the boundaries.
Examples & Analogies
Think of a cylindrical tank filled with water where water is flowing in through one pipe and out through another pipe. The tank represents your control volume, and the paths that the water takes as it flows in and out can be visualized using imaginary lines—these are the streamlines.
Understanding Influx and Outflux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if I look at simple definitions, the calculus is that the time rate of change of B in the system as a definition t + dt minus the system at the t level...
Detailed Explanation
This chunk discusses how to define influx (the flow into a control volume) and outflux (the flow out of it) in terms of time rates of change. It emphasizes the mathematical representation of these flows and how they relate to the conservation of mass and energy. This understanding is crucial for applying control volume analysis effectively.
Examples & Analogies
Imagine a bathtub being filled and drained at the same time. The water flowing in is your influx, while the draining water represents your outflux. By studying the rates at which water flows in and out, you can determine how quickly the bathtub is filling or emptying.
Integrating for Total Flux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I want to compute the outflux surface, okay? That means, assuming it is a three-dimensional control volume, and over that surface I want to integrate it...
Detailed Explanation
This chunk covers the integration process used to compute mass or energy flow rates through the surface of a control volume. It describes how to consider small area elements of the control surface and how to integrate them to find total outflux or influx, using velocity and surface area in the calculations.
Examples & Analogies
Consider a garden hose: when you turn on the water, it's flowing through the nozzle (outflux). If you wanted to calculate how much water is coming out over a certain period, you could measure the water flow rate at different small sections of the hose and add them all together—similar to how you integrate to find total flux.
Applying Steady Flow Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us come back to very simple case that we can do, the steady incompressible flow...
Detailed Explanation
This chunk explains how to simplify the analysis of fluid flows by applying steady-state conditions. In steady incompressible flow, the fluid density doesn't change with time, allowing for easier calculations and integration when analyzing control volumes—often making calculations significantly simpler.
Examples & Analogies
Think of a steady river flow where the amount of water entering an area is equal to the amount leaving. Because the flow rate doesn't fluctuate over time (steady), you can easily measure the water's speed and predict how much will pass a certain point without having to worry about changing conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Control Volume Analysis: A method for analyzing fluid behavior within a defined region.
-
Conservation Laws: Principles governing mass, momentum, and energy in fluid mechanics.
-
Extensive Properties: Properties dependent on the total mass of the system.
-
Intensive Properties: Properties independent of the mass, such as density.
-
Reynolds Transport Theorem: A theorem that links the changes in a system to the flow of properties across a control volume.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Analyzing water flow through a pipe using control volume analysis to demonstrate changes in mass and energy.
-
Calculating the velocity of fluid entering and leaving a tank, applying conservation laws.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the fluid's flow, what do we see? Mass, momentum, energy keep company.
📖 Fascinating Stories
-
Imagine a river as a control volume, where fish can't just disappear and energy flows like the currents changing direction.
🧠 Other Memory Gems
-
MEM: Mass, Energy, Momentum — the three flows we must pay attention.
🎯 Super Acronyms
RTT
- Relates Time and Transport — use it to analyze flow in your report.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A defined region in space through which fluid can flow, used for analyzing fluid motion and properties.
-
Term: Conservation of Mass
Definition:
The principle stating that mass is neither created nor destroyed in a closed system.
-
Term: Conservation of Momentum
Definition:
The principle stating that the total momentum of a closed system remains constant unless acted on by external forces.
-
Term: Conservation of Energy
Definition:
The principle stating that energy cannot be created or destroyed, only transformed from one form to another.
-
Term: Extensive Properties
Definition:
Properties of a system that depend on its mass, such as energy and momentum.
-
Term: Intensive Properties
Definition:
Properties of a system that do not depend on its mass, such as density and temperature.
-
Term: Reynolds Transport Theorem (RTT)
Definition:
A mathematical framework relating the flow of properties within a control volume to the changes in a system.