Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Establishing Basic Fluid Principles
Unlock Audio Lesson
Today, we'll discuss the foundational principles of fluid dynamics, specifically conservation laws — mass, momentum, and energy. Can anyone tell me what they understand by conservation laws in fluid dynamics?
I think conservation laws mean that in any closed system, certain quantities remain constant over time.
Exactly, Student_1! Conservation laws imply that mass, momentum, and energy are conserved in a fluid system, unless acted upon by external forces. This concept helps us understand fluid behavior in different environments.
How do we apply these laws practically in systems?
Great question! We apply these laws through control volume analysis, where we analyze the fluid flow entering and exiting a defined volume. This leads us to the derivation of the Reynolds Transport Theorem, which connects these principles at the system level to those at the control volume level.
I'm curious about how extensive and intensive properties fit into this.
An excellent point! Extensive properties, like mass and energy, are directly dependent on the amount of matter in the system, whereas intensive properties, like velocity, do not change with mass. Understanding these differences is crucial for our next steps.
What are some examples of these properties?
For example, energy is an extensive property, while specific energy is intensive. Remember, extensive properties increase with mass, while intensive properties stay constant. Let’s summarize: conservation laws apply to closed systems, and understanding properties sets the stage for deriving the Reynolds Transport Theorem.
Understanding the Reynolds Transport Theorem
Unlock Audio Lesson
Now, let’s dive into the Reynolds Transport Theorem itself. Who can summarize why RTT is important?
RTT helps us relate the changes in properties at the system level to the changes observed within a control volume?
Exactly, Student_1! RTT provides a mathematical representation connecting the extensive property changes between systems and control volumes. It’s crucial for fluid dynamics applications!
Could you explain how we derive RTT using control volumes?
Of course! We begin with a control volume that may change over time. We consider the state of the fluid in the control volume at two different times and relate the extensive property 'B' over this volume to its influx and outflux.
Are the influx and outflux treated differently in the derivation?
Yes! Influx is considered positive when entering the control volume, and outflux is negative when leaving. This sign convention is critical for obtaining accurate results.
What about the equations? Do they get complicated?
While they can appear intricate, the essence is that the change of B in the system is equal to the accumulation of B in the control volume and the net outflux through the control surface. Let’s summarize: the RTT connects fluid behavior between systems and control volumes, maintaining sign conventions for influx and outflux!
Applying RTT to Real-World Scenarios
Unlock Audio Lesson
Now, let’s discuss how we can apply the Reynolds Transport Theorem to real-world fluid dynamics scenarios. What kind of flow examples should we consider?
We could think about water flowing through a pipe, right?
Absolutely, Student_2! In pipe flow, the RTT allows us to analyze how fluid enters and leaves the system and calculate flows efficiently. What about in terms of control volumes?
Maybe something like a tank filling or draining?
Exactly! When a tank is filling, we can use the RTT to relate the volume of water entering to the height change in the tank. This helps in designing systems that need accurate flow measurements.
What kind of calculations do we perform in these scenarios?
We can calculate flow rates, average velocities, and analyze the changes in velocity as the fluid moves through different sections of the pipe or tank. Remember, practice makes it easier!
So, it's all about applying RTT mathematically to see how we manage our fluids, right?
Exactly, Student_4! The RTT helps simplify the very complex relationships in fluid flow and brings everything together. Let’s recap: RTT is fundamental for understanding how fluids operate in practical situations, including calculating flow rates and analyzing tank filling or drainage!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the fundamental concepts of extensive and intensive properties, outlines the Reynolds Transport Theorem, and explains its significance in connecting system-level and control volume dynamics. Key elements include the definitions of properties, their relationships, and the mathematical foundation for the theorem.
Detailed
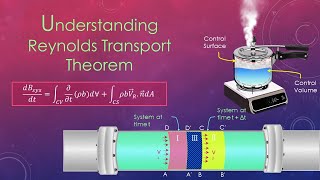
Derivation of Reynolds Transport Theorem
The Reynolds Transport Theorem (RTT) serves as a bridge between the conservation principles at the system and control volume levels in fluid dynamics. It encompasses three primary conservation laws: mass conservation, momentum conservation, and energy conservation. In this section, extensive and intensive properties are defined, highlighting their dependence on mass.
Properties Defined
- Extensive properties (e.g., mass, momentum, energy) are linearly proportional to the quantity of material in the system. For instance, if mass increases, the extensive property also increases.
- Intensive properties (e.g., velocity, specific energy) remain constant regardless of the amount of substance, and reflect a per-unit basis.
Understanding these distinctions is crucial as they provide the mathematical foundation for deriving the RTT, which involves careful analysis of a control volume. By categorizing the system's influx, outflux, and the change within the volume from one time increment to the next, the RTT mathematically describes how properties change based on the control surface interactions.
The section concludes with practical examples and applications of the RTT in various flow scenarios, emphasizing its importance for fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Conservation Principles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The conservation of momentum which is required for you to know it, how the fluid particles are moving it, what could be the force exerting on that, what could be the velocity. Similar way, we can understand the energy conservation which plays a major role for us when the fluid comes from one location to other locations, how much of work is done by the fluid or into the fluid. Similar way, whether there is heat transfers happening which you can feel it...
Detailed Explanation
This chunk introduces the fundamental principles of conservation that are vital in fluid mechanics such as the conservation of mass, momentum, and energy. These principles form the basis for analyzing any fluid system. In fluid dynamics, understanding how these quantities behave as fluid moves is crucial for solving real-world problems in engineering and science. The flow of fluid involves considerations of forces acting on the fluid particles, work done by or on the fluid, and heat transfers that happen as fluids interact with their environments.
Examples & Analogies
Imagine a river flowing from a mountain to a lake. As the water flows, it carries momentum (due to its mass and velocity), does work by eroding the river banks (energy conservation), and can transfer heat to the surrounding air or ground. Understanding how the water conserves its energy, momentum, and mass helps in predicting how the river will behave under different conditions, such as during a heavy rain.
Extensive vs. Intensive Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let me define two types of properties that we have; one is called extensive property and the other is intensive property... Extensive property is proportional to the amount of mass. For example, mass conservation, momentum conservation, and energy conservation. Intensive properties, that means it is independent of mass...
Detailed Explanation
In this chunk, we define extensive and intensive properties. Extensive properties are those that depend on the amount of fluid present (e.g., mass, volume, energy), meaning if you have more fluid, these properties increase. Conversely, intensive properties do not depend on the size or mass of the system (e.g., temperature, pressure, and density). Understanding these properties is crucial because it helps in applying the right equations in fluid mechanics problems.
Examples & Analogies
Think of extensive properties like the total amount of frosting on a cake—a larger cake (more mass) means more frosting (extensive property). In contrast, the frosting's sweetness is an intensive property, which does not change regardless of the cake's size. Whether you have a small cupcake or a large wedding cake, the sweetness remains constant.
Derivation Overview of Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
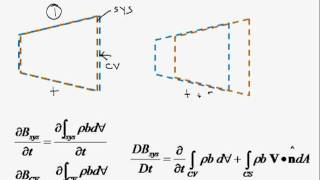
Now, we will go to derive Reynolds transport theorem. The derivation of the Reynolds transport theorem are available in almost all the fluid mechanics books... So, first, what we are considering is a non-deforming control volume.
Detailed Explanation
This segment outlines the beginning of the derivation for the Reynolds Transport Theorem (RTT). The RTT connects the conservation laws at a system level and a control volume level, essential for analyzing fluid motion. The control volume is typically a fixed or non-deforming volume through which fluid flows in and out. Understanding how the fluid's total property changes both at the system level and control volume level is crucial for solving fluid dynamics problems.
Examples & Analogies
Consider a water tank connected to a pipe. The water flowing in and out represents the control volume. RTT helps us understand how the volume of water changes in this tank based on the flow rates into and out of the tank. By understanding the total volume (system) versus the volume inside the tank (control volume), we can predict how long it takes to fill up or empty the tank.
Control Volume Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
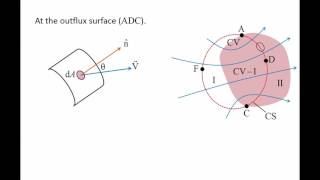
...I can define there will be a control surface defined by A, D, C, and F... the streamlines are indicating how the influx is coming into the control volume and going out from the control volume, through this surface.
Detailed Explanation
Here, we discuss the definition of a control volume, which is the specific region in space where we analyze the fluid motion. The control surface is the boundary that defines this control volume. Understanding the influx (fluid entering) and outflux (fluid exiting) is essential for applying the conservation principles and helps in deriving the equations governing fluid flow.
Examples & Analogies
Continuing with our water tank example, the walls of the tank represent the control surface. The water entering through the pipe is the influx, while the water leaving through a drain is the outflux. By observing the flow in this fixed volume, we can analyze how the water levels change over time.
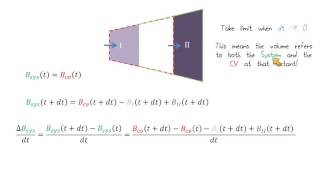
Deriving dB Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if I look at simple definitions... dB B (t + dt) - B (t) / dt.
Detailed Explanation
In this step of the derivation process, we introduce 'dB', which represents the change in an extensive property (like mass, momentum, or energy) per unit time within the system. The change is calculated over a time interval 'dt'. This mathematical relationship sets the stage for how we will relate the properties at the system level with those at the control volume level.
Examples & Analogies
Think about filling a bathtub. If you turn on the faucet and track the change in water level over a minute, that change can be expressed as dB per time. Just like measuring how much water fills the tub as time passes gives you an insight into the change in the water level, understanding dB gives insight into how mass or energy changes in our control volume over time.
Flux Calculation Through Control Surface
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, how to compute the outflux surface... that means how much of influx is coming into the control volume or going out from control volume.
Detailed Explanation
Here, we discuss how to calculate the influx and outflux of fluid through the control surface. This involves considering the velocity vector and the area vector at each point of the surface. The calculations define how much fluid passes through per unit time based on the geometry of the control volume and the velocity of the fluid, helping to fully characterize the fluid behavior through the control volume.
Examples & Analogies
Let's say we are measuring how fast water is flowing out of a garden hose. By knowing the diameter of the hose and the speed of the water, we can calculate the total volume of water flowing out per minute. This is analogous to calculating outflux across the control surface.
Final Expression of Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, coming to the third part. The first two terms we can write it as earlier you will have the influx and outflux...
Detailed Explanation
This part brings together the various elements of the derivation and expresses the Reynolds Transport Theorem mathematically. The theorem essentially states that the rate of change of a property within a control volume is equal to the net influx of that property into the control volume, which combines all previously discussed concepts of influx, outflux, and time rate changes.
Examples & Analogies
Imagine you are filling a swimming pool with water from a hose while some water is also leaking out through a crack. The RTT helps you determine whether the water level will increase, stay the same, or decrease based solely on the rates of water flowing in and leaking out.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Conservation Laws: Fundamental principles in fluid dynamics governing mass, momentum, and energy.
-
Extensive vs. Intensive Properties: Classification of properties dependent or independent on mass.
-
Control Volume Analysis: A method to evaluate fluid flow by defining a specific volume through which fluid passes.
-
Reynolds Transport Theorem: A mathematical expression that connects system and control volume property changes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of water flowing through a pipe: Analyze the inflow and outflow rates at different points.
-
Example of a tank draining: Use RTT to understand the changes in water level over time as water exits.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In flows that twist and turn, conservation is our main concern.
📖 Fascinating Stories
-
Imagine a river that flows steadily. As it encounters a dam (control volume), water builds up (influx), but when it releases through the gates (outflux), the level drops. This story illustrates how we analyze flows using the RTT.
🧠 Other Memory Gems
-
EIE: Extensive increases with extra mass; Intensive is fixed, can't bypass.
🎯 Super Acronyms
RTT
- Relating Total Transport in theorems.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Reynolds Transport Theorem (RTT)
Definition:
A theorem that connects the changes in properties of a system to those in a control volume, incorporating the concepts of flux.
-
Term: Extensive Property
Definition:
A property that scales with the amount of mass in the system (e.g., mass, momentum, energy).
-
Term: Intensive Property
Definition:
A property that remains unchanged regardless of the amount of mass (e.g., temperature, pressure, specific energy).
-
Term: Control Volume
Definition:
A defined space through which fluid flows, used to analyze fluid motion and properties.