Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Flow Conservation Laws
Unlock Audio Lesson
Today, we will look into conservation laws in fluid dynamics, particularly focusing on mass, momentum, and energy. Why do you think these laws are important for understanding fluid flows?
They help us figure out how fluids behave when they move and interact, right?
Exactly! These laws help predict the state of a fluid system. We often use these concepts in what’s known as control volumes and systems.
What’s the difference between a control volume and a system?
A system refers to the mass within a boundary, while a control volume is a defined space through which fluid flows, allowing us to analyze the interactions at the boundaries.
So, we can see how properties change at the surface then?
Yes, and that leads us perfectly into Reynolds Transport Theorem, which correlates these changes with conservation laws!
As a summary, conservation laws help define how fluids behave, using systems and control volumes allows us to analyze the flow dynamics effectively.
Understanding Extensive and Intensive Properties
Unlock Audio Lesson
Let’s dive deeper into the types of properties we mentioned: extensive and intensive. Can anyone define what extensive properties are?
They’re properties that depend on the amount of mass, right?
Correct! Examples include total mass and energy. Now, what about intensive properties?
Those are independent of mass, like density and temperature?
Exactly! They help us understand the state of a substance per unit mass. Remember, for energy, the extensive property is total energy while the intensive is specific energy.
Can you give a real-world example of using these concepts in fluid flow?
Sure! When designing a pipeline, understanding how much fluid (mass, extensive) flows and its pressure, temperature (intensive) at certain points helps in creating efficient systems.
In summary, distinguishing between extensive and intensive properties is essential for analysis in fluid mechanics, particularly in applying the Reynolds Transport Theorem.
Deriving Reynolds Transport Theorem
Unlock Audio Lesson
Now let's move on to the derivation of the Reynolds Transport Theorem. Why is it essential to understand its derivation?
It shows how we get from conservation principles to practical equations for analyzing fluid flow.
Exactly! RTT connects what happens in a closed system to a control volume, outlining how we can quantify changes over time. Can anyone recall the three main components we need to derive this theorem?
We need to consider the time rate of change, influx, and outflux.
Right! The time rate of change of an extensive property in the system relates to the accumulation in the control volume and the net flow through its boundaries.
What does that look like mathematically?
"It can be represented as:
Applications of the Reynolds Transport Theorem
Unlock Audio Lesson
As we’ve learned RTT, how do you think this theorem applies to real-world scenarios?
It can help calculate flow rates in pipes or channels, right?
Precisely! By analyzing how properties change across control volumes, engineers can optimize designs. Can someone give an example of a specific application?
Like in designing a river dam! We can use it to manage water flow and pressure.
Fantastic example! Additionally, in aerospace, RTT is used in understanding airflow around aircraft wings.
How does understanding RTT make the design process more efficient?
It helps identify where losses may occur and optimizes performance. To summarize, RTT's practical applications in designing systems across various fields highlight its significance in fluid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces the Reynolds Transport Theorem, emphasizing the relationship between conservation principles at the system versus control volume levels. It distinguishes between extensive and intensive properties while explaining the significance of understanding these concepts in fluid dynamics.
Detailed
Detailed Summary
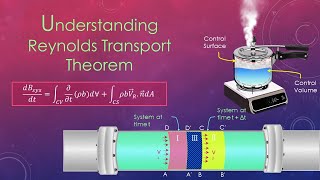
The Reynolds Transport Theorem (RTT) serves as a critical bridge in fluid mechanics, linking conservation laws at the system level with those at the control volume level. It encapsulates three vital conservation principles: the conservation of mass, momentum, and energy.
At the heart of the RTT is the distinction between extensive and intensive properties. Extensive properties are dependent on the amount of mass in a system (e.g., total mass, total momentum, or total energy), while intensive properties are independent of mass (e.g., density, velocity, or specific energy). The theorem articulates how the time rate of change of an extensive property in a closed system relates to the influx and outflux of this property through a defined control volume.
Furthermore, the document elaborates on the mathematical derivation of RTT, focusing on non-deforming control volumes, influx, and outflux definitions, and how to evaluate these terms using surface integrals. The RTT is foundational for analyzing various fluid flow scenarios, including steady and unsteady conditions, providing insights into the conservation of quantity across different regions in fluid mechanics. Understanding this theorem significantly aids in solving complex fluid flow problems and deriving essential equations in fluid dynamics.
Youtube Videos
![Get to know Reynolds Transport Theorem - part I [Fluid Mechanics]](https://img.youtube.com/vi/BwOnHIsgK_Q/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Conservation Principles in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similar way, we can understand the energy conservation which plays a major role for us when the fluid comes from one location to other locations, how much of work is done by the fluid or into the fluid.
Detailed Explanation
This chunk describes the fundamental principles of conservation in fluid mechanics. Specifically, it highlights three major conservation laws: conservation of mass, momentum, and energy. Each principle applies to fluid systems in a similar manner as they do in solid mechanics. The conservation of energy, for example, is crucial for determining how much work a fluid does while moving from one place to another, and how it can transfer energy into or out of a system.
Examples & Analogies
Think of water flowing through a pipe. As it moves from a higher elevation to a lower one, it does work by turning a water wheel, generating energy. This visualizes the principle that as fluids move, they carry energy and momentum with them.
Extensive and Intensive Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let me define two types of properties that we have; one is called extensive property and the other is the intensive property.
Detailed Explanation
This chunk introduces the distinction between extensive and intensive properties. Extensive properties depend on the size or mass of the system, such as mass, momentum, or energy. In contrast, intensive properties, such as temperature or pressure, remain constant regardless of the system's size. This distinction is crucial in understanding how different properties behave under varying conditions in fluid mechanics.
Examples & Analogies
Consider a glass of water. The total mass and energy (extensive properties) depend on how much water is in the glass. However, the temperature (an intensive property) would be the same whether it’s a full glass or just a drop.
The Definition of Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
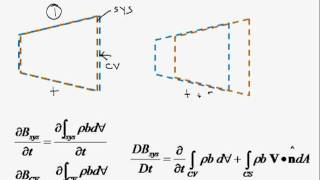
Now, we will go to derive Reynolds transport theorem. The derivation of the Reynolds transport theorem are available in almost all the fluid mechanics books.
Detailed Explanation
The Reynolds transport theorem (RTT) connects the concepts of fluid motion and conservation laws at both system and control volume levels. It provides a mathematical framework to analyze how extensive properties change within a control volume as fluid enters and exits the system. By establishing this theorem, we can apply it to various problems in fluid mechanics.
Examples & Analogies
Imagine a container filled with gas. As gas molecules flow in and out, the RTT helps us quantify how much gas is present inside at any given time, even as the influx and outflux vary. This is similar to a busy restaurant, where people continually enter and leave, yet you can still keep a count of how many customers are being served at any moment.
Three Regions in Control Volume Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
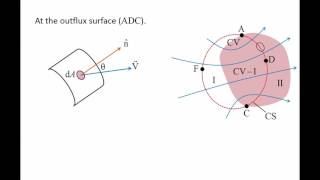
I can define this 3 into 3 different spaces, like the space defined by this part I can give it as I and this can be II and this can be used as the control volume space.
Detailed Explanation
This segment discusses how, during a control volume analysis, the fluid domain can be divided into three distinct regions: the influx region, outflux region, and the overlapping region where fluid exists at both present time t and future time t + dt. This division assists in understanding how fluid properties change over time and how to analyze the net changes in these properties.
Examples & Analogies
Think of it like a bathtub. The area where water is entering is the influx, where it is draining is the outflux, and the amount of water that remains after a certain time is the space that overlaps. This visualization makes it easier to understand how changes in input and output affect the overall water level.
Mathematics of Flux through Control Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, how to compute the outflux surface, okay? That means, assuming it is a three-dimensional control volume, and over that surface I want to integrate it...
Detailed Explanation
This section deals with the mathematical computation of fluid flux through the surfaces of a control volume. By considering small surface elements and their associated normal vector and velocity, one can use calculus to integrate values over the control surface, which allows for the calculation of the total influx or outflux of the fluid.
Examples & Analogies
Imagine a water slide at a park where kids are going down. Each section of the slide has a specific number of kids going down in a given time. By observing each section of the slide as a control volume, we can calculate how many kids are sliding down (outflux) versus how many are approaching the top (influx).
Final Formulation of Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
That is what is Reynolds transport theorem, and the basic physics you can understand.
Detailed Explanation
In the conclusion of the RTT discussion, we frame the theorem succinctly: the rate of change of a property within a system is equal to the accumulation of that property in a control volume plus the net outflux through its boundary. This serves as a powerful tool for solving complex fluid dynamic problems by linking the behaviors of the system with control volume analysis.
Examples & Analogies
Returning to our bathtub example, if we think of it in terms of how full the tub is (the system), we can account for the water that flows in from the faucet and what flows out from the drain (the control volume), giving us a complete picture of how the water level changes over time.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Conservation Laws: Principles that dictate that energy, mass, and momentum are conserved in fluid systems.
-
Extensive vs. Intensive Properties: Extensive properties depend on the size of the system, while intensive properties are size-independent.
-
Control Volume: An enclosed area in space wherein fluid flow is analyzed to understand dynamics and conservations.
-
Reynolds Transport Theorem: A formula connecting the changes in extensive properties within a system to fluxes across the control volume.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When analyzing water flow in a pipe, the total mass flow rate can be computed using RTT, allowing engineers to optimize pipe dimensions.
-
In aviation, engineers apply RTT to study airflow around wings, which assists in aerodynamic design to improve lift and reduce drag.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When mass is your cue, extensive comes through, / Intensive stands tall, with no mass to call.
📖 Fascinating Stories
-
Imagine a flowing river. The water levels rise and fall (extensive) while the temperature remains consistent (intensive). This interplay reflects how RTT operates across nature!
🧠 Other Memory Gems
-
Remember: E for Extensive (E), M for Mass; I for Intensive (I), Independence at last!
🎯 Super Acronyms
RTT - Relating Time and Transport of flux, encompassing mass, momentum, and energy.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that relates the time rate of change of an extensive property in a system to the flow of that property into and out of a control volume.
-
Term: Extensive Property
Definition:
A property that depends on the amount of mass in a system, such as mass, momentum, and energy.
-
Term: Intensive Property
Definition:
A property that is independent of the mass of the system, such as density and specific energy.
-
Term: Control Volume
Definition:
A defined region in space through which fluid can flow, used to analyze the behavior of fluids.
-
Term: Conservation Laws
Definition:
Fundamental principles that state certain properties remain constant within a system as long as it is closed.