Applications of Dimensional Analysis
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Dimensional Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome to today's session. Let's begin with an important tool in fluid mechanics: dimensional analysis. This tool enables us to validate equations or derive new relationships among variables by using units.

How does dimensional analysis help us with real-world problems?

Great question! By reducing complex relationships into dimensionless forms, we can simplify our understanding of flow behaviors in different conditions. For example, when studying river hydraulics, we can predict how large-scale flows might behave based on small-scale models.

Can you explain what you mean by dimensionless forms?

Certainly! A dimensionless form means that the variables under consideration have been normalized. For instance, using the Reynolds number allows us to analyze the flow regardless of the specific conditions, ensuring we can make valid comparisons.

So, does it mean we can test on smaller scales to predict larger outcomes?

Exactly! Just like in our lab models of the Brahmaputra river, where we scale down dimensions.

That sounds fascinating! So, both geometric and dynamic similarities are essential?

Yes, they are! Let's move to that next. To summarize, dimensional analysis helps simplify complex fluid interactions and check the validity of numerical models.
Geometric and Kinematic Similarity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

As we dive deeper, let’s discuss geometric and kinematic similarities. Can anyone tell me what geometric similarity means?

Geometric similarity means the model replicates the exact proportions of the prototype, right?

Exactly! By maintaining the same ratios, we ensure that the flow patterns observed in the model reflect those of the prototype. Now, what about kinematic similarity?

Isn't that when the flow velocities and streamline patterns are analogous?

You got it! Kinematic similarity ensures that the same types of flows occur in both scenarios. This fundamental comparison is crucial for experiments, especially when working on civil engineering projects.

I see! What are the implications for fluid models?

By understanding these concepts, engineers can scale experiments to predict behaviors without needing full-scale models, which might be impractical. For example, say we scale a dam model down to 1:100, it still accurately represents flow physics.

I guess it saves time and resources as well!

Absolutely! To summarize, geometric and kinematic similarities are vital for translating model findings to real-world predictions.
Bernoulli’s Equation and Dimensional Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s explore how dimensional analysis applies to Bernoulli’s equation. Who can remind us of its significance in fluid dynamics?

It shows the relationship between pressure, velocity, and height in fluid flow?

Exactly! Now, when we conduct dimensional analysis on Bernoulli’s equation, what do we look to check?

We look for dimensional homogeneity in the equation!

Right! By ensuring each term has the same dimensions, we can validate that our equation is correct. Let’s consider how energy conservation principles apply here.

Do similar checks apply to other equations as well?

Yes! The process of validating equations using dimensional analysis is universal throughout fluid mechanics. Indirectly, it helps us understand conservation principles and flow behaviors.

That’s very important for our engineering calculations!

Indeed! In summary, verifying Bernoulli’s equation through dimensional analysis showcases its reliability in various fluid systems.
Applying Dimensional Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's discuss practical applications of dimensional analysis further. Can anyone provide an example where it might be critical?

When designing a new dam, we need accurate flow predictions based on scaled-down models!

Correct! In those instances, both geometric and dynamic similarities must be maintained. What role does the Froude number have in such cases?

The Froude number helps maintain similarity between models and prototypes in free surface flows!

Well done! It compares inertial forces to gravitational forces. Keeping these ratios consistent is crucial for predictions to be valid.

And it’s essential for predicting wave behaviors in modeling too.

Very true! Practical implementations using dimensional analysis streamline the engineering process and promote accuracy.

I can see its importance in our future work.

To conclude, implementing dimensional analysis in fluid mechanics enhances design precision and fosters understanding of complex systems.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Dimensional analysis is crucial in fluid mechanics for validating equations and conducting physical models, facilitating the understanding of fluid properties and flow behavior in both scaled-down laboratory environments and real-world applications. The discussion also highlights similarities and the application of Bernoulli’s equation.
Detailed
Applications of Dimensional Analysis
Dimensional analysis plays a pivotal role in the field of fluid mechanics, particularly in validating complex equations, performing physical modeling experiments, and ensuring dimensional homogeneity across equations. This section initially introduces physical modeling experiments, where real-world scenarios, like those of the Brahmaputra river, are scaled down into manageable prototypes for safer and cost-effective study.
The concept of geometric, kinematic, dynamic similarities, and thermal similarities are introduced as vital aspects of the dimensional analysis that helps in establishing relationships between model and prototype interactions. The relationship between these similarities can be effectively used for establishing design parameters which ensure that experiments can accurately replicate real-world phenomena.
In addition, the analysis of Bernoulli's equation highlights how to utilize dimensional analysis for checking the correctness and validity of the derived equations in understanding fluid behaviors. Throughout the discussions, the significance of applying non-dimensional numbers such as Reynolds and Froude numbers is emphasized in achieving kinematic and dynamic similarities. Overall, dimensional analysis is essential for predictive modeling in fluid dynamics, leading to successful design and functioning of hydraulic structures.
Youtube Videos


![[Fluid Dynamics: Dimensional Analysis] Applications and Examples](https://img.youtube.com/vi/nFswey9fMXU/mqdefault.jpg)


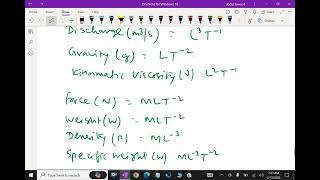




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Dynamic Similarity and Its Importance
Chapter 1 of 1
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Dynamic similarity is achieved when the forces acting on a model and its prototype are proportional, which often requires geometric and kinematic similarity as prerequisites.
Detailed Explanation
Dynamic similarity considers the balance of forces acting on both the prototype and model. When forces such as pressure, gravity, and viscosity act similarly in both systems, we have achieved dynamic similarity. This concept allows engineers to predict that the model's performance will accurately reflect that of the full-size prototype under comparable conditions.
Examples & Analogies
Imagine two pools of water where one is a small dog bowl and the other is an Olympic-sized swimming pool. If you pour water into both, the dynamics of waves, splashes, and movements should proportionally match when similar forces (like how forceful the pour is) are applied. Achieving dynamic similarity means that any observations made in the dog bowl can help predict the behavior of water in the larger swimming pool.
Key Concepts
-
Dimensional Analysis: Used to simplify complex physical relationships and validate equations.
-
Geometric Similarity: Ensures the model maintains the same geometry ratios as the prototype.
-
Kinematic Similarity: Ensures similar velocity and streamlines between model and prototype.
-
Dynamic Similarity: Ensures the same force interactions for the model and prototype.
-
Bernoulli’s Equation: Models conservation of energy in fluid flow scenarios.
Examples & Applications
A scaled-down model of a river used to predict flood behavior.
Using dimensional analysis on Bernoulli's equation to validate its accuracy across different flow scenarios.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Dimensional analysis, oh what a delight, simplifies, validates, makes equations right.
Stories
Once upon a time in an engineer's lab, they built models to explore flow, all in fab! Dimensional analysis was their trusty guide, revealing secrets of fluid with every tide.
Memory Tools
When you check your equations, remember G, K, D: Geometric, Kinematic, Dynamic similarity!
Acronyms
GKD - Geometric, Kinematic, Dynamic - the triad of similarity in fluids!
Flash Cards
Glossary
- Dimensional Analysis
A mathematical approach to analyzing the dimensions of physical quantities to test the validity of equations.
- Geometric Similarity
A condition where the model and prototype maintain the same geometric ratios.
- Kinematic Similarity
A condition where the velocity and streamlines of the model and prototype are similar.
- Dynamic Similarity
A condition where forces acting on the model and prototype are balanced in terms of their magnitudes and directions.
- Bernoulli’s Equation
An equation describing the principle of conservation of energy in fluid flow.
- Reynolds Number
A dimensionless number used to predict flow patterns in different fluid flow situations.
- Froude Number
A dimensionless number that compares inertial forces to gravitational forces in fluid flows.
- Dimensional Homogeneity
A property of an equation wherein all terms have the same dimensional units.
Reference links
Supplementary resources to enhance your learning experience.
