Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Dimensional Analysis
Unlock Audio Lesson
Good morning class! Today, we will delve into the significance of dimensional analysis in fluid mechanics and look closely at Bernoulli's equation. Dimensional analysis helps us confirm whether equations make sense by checking if the units are homogeneous. What does that mean, Student_1?
It means that all the terms in an equation should have the same units, right?
Exactly! So, if we have pressure, velocity, and height in an equation, they should all relate dimensionally. Can anyone give me an example of a dimensionally homogeneous term?
Pressure has dimensions of force per unit area, which can be expressed as mass times acceleration divided by area!
Great example! We can express mass as density times volume, exposing how they interact. Remember the acronym 'M.A.P.' for Mass, Area, and Pressure as we go through this section.
Exploring Bernoulli's Equation
Unlock Audio Lesson
Now, let’s move on to Bernoulli's equation. This equation relates velocity, pressure, and height in a flowing fluid. Can anyone tell me what Bernoulli's equation looks like?
I think it’s something like P + 0.5ρv^2 + ρgh = constant, where P is pressure, ρ is density, v is velocity, and h is height.
"Correct! So when we check dimensional homogeneity, the pressure term P has units of force per area, the kinetic energy term
Physical Interpretation of Bernoulli's Equation
Unlock Audio Lesson
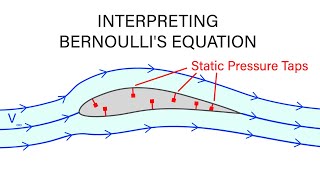
Let’s take a moment to think about how Bernoulli's equation helps us understand fluid flow in real-life scenarios such as dams or rivers. Why is it useful, Student_2?
It helps us predict how changes in speed or elevation affect pressure in the fluid!
Exactly! For instance, when water flows through a dam, faster flow areas have lower pressure, which can lead to erosion over time. What kinds of experiments do you think we would do to analyze this?
We could use physical models to simulate the flow and measure pressures at different points!
Excellent point! Always remember how dimensional analysis empowers us to scale these experiments correctly.
Implications of Dimensional Analysis on Modeling
Unlock Audio Lesson
Today, we see how dimensional analysis not only validates our equations but also guides physical models. How might we apply this in a dam project, Student_4?
We could use scaled-down models to analyze how the dam will behave under various flow conditions!
Right, if we understand the kinematic similarity, we can ensure our models accurately predict behavior under similar flow conditions. Who remembers the terms we use for different types of similarity?
Geometric, kinematic, and dynamic similarity!
Fantastic! Remembering these similarities helps in creating accurate models and validating results through dimensional analysis is critical.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the relationship between dimensional analysis and Bernoulli’s equation is dissected to understand how physical properties influence flow behavior. Key properties such as pressure, velocity, and discharge are examined, alongside the importance of identifying dimensional homogeneity in equations.
Detailed
Dimensional Analysis of Bernoulli's Equation
In fluid mechanics, particularly when analyzing Bernoulli's equation, dimensional analysis serves as a critical tool to verify the correctness of derived equations. This section emphasizes the necessity of ensuring that all terms in an equation exhibit dimensional homogeneity, meaning they share the same units.
Key Points:
- Dimensional Properties: Basic dimensions in fluid mechanics include length, area, volume, velocity, and pressure. Each of these can be expressed through fundamental units, and their relationships define fluid behavior.
- Application of Dimensional Analysis: By substituting dimensions into complex equations, one can confirm if the equations are consistent. This practice is especially relevant when working with Bernoulli's equation, which describes the conservation of energy in flowing fluids.
- Understanding Bernoulli's Equation: The equation can be expressed under various conditions (steady, incompressible flow) and by analyzing its terms, we observe the conservation laws at play, ensuring that they are dimensionally consistent. This promotes better model representation in practice.
Overall, understanding dimensional analysis in the context of Bernoulli's equation is crucial for engineers and students to validate their mathematical models and physical interpretations within fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us coming to the dimensions of the fluid mechanics properties, as discussed in the last class, I am just repeating it that you have the dimensions of basic geometry which in terms of length, area, volume.
Detailed Explanation
In fluid mechanics, we often use Bernoulli's equation, which describes the principles of fluid flow. Understanding the dimensions of various properties involved is crucial. Dimensions in this context refer to basic geometric quantities such as length, area, and volume that help describe the behavior of fluids in motion.
Examples & Analogies
Think of Bernoulli's equation like a balance scale for fluids. Just as a scale measures weight in pounds or kilograms, Bernoulli's equation measures fluid behavior in terms of length and area to ensure everything is balanced and functioning properly.
Form of Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at the unsteady frictionless flow along a streamline which is the Bernoulli’s equations, it look it in terms of differences, the integrations part and all the things substitute the dimensions.
Detailed Explanation
Bernoulli's equation describes the conservation of energy in a flowing fluid. It relates pressure, velocity, and height at different points along a streamline. When we talk about unsteady flow, we recognize that changes can occur. Substituting dimensions into the equation allows us to analyze these variations and ensures that energy is conserved throughout the flow.
Examples & Analogies
Imagine water flowing through a garden hose. When you cover part of the hose with your thumb, the water speeds up due to the change in pressure. Bernoulli's equation helps us understand how this change happens and ensures that the total energy (like speed and pressure) remains consistent, much like maintaining a steady pace in a relay race!
Dimensional Homogeneity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Each terms having the same dimensions. Substitute that, I just encouraged the students have these practise, wherever you derive the equations, just spends few minutes to write the dimensions of these variables.
Detailed Explanation
When dealing with equations in fluid mechanics, it is important to check the dimensional homogeneity. This means that all terms in the equation must have the same dimensions. This practice helps verify that an equation is set up correctly, indicating that the relationship between the different quantities is valid and consistent.
Examples & Analogies
Think about making a cake. If you use cups, tablespoons, and teaspoons all together without ensuring they are compatible, your cake might not turn out well. Similarly, ensuring that all terms in an equation have compatible 'dimensions' guarantees a valid result in fluid equations.
Applications of Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you go for a simple model this is what called a very, it is not a complex that merge, but we can say that having integrations and all the fact.
Detailed Explanation
Bernoulli's equation is widely applied in various fields, including engineering and environmental science. By integrating this equation, we can analyze fluid behavior in situations such as airplane wings, water pipelines, and even natural rivers. The findings help engineers design structures that can efficiently handle fluid flow.
Examples & Analogies
Consider how an airplane wing works. The shape of the wing creates different air velocities above and below it, which leads to differences in pressure as described by Bernoulli's principle. This is what helps the plane to lift off the ground, just as it helps us understand why a straw sucks up liquid—both rely on the same principles of fluid dynamics!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dimensional Analysis: A technique to evaluate the dimensions of physical quantities in equations.
-
Bernoulli's Equation: A fundamental equation in fluid dynamics that relates pressure, velocity, and height.
-
Dimensional Homogeneity: A critical aspect of ensuring correctness in mathematical formulations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of pressure in a fluid system where height influences pressure.
-
Example of measuring flow rate in a pipe and its relation to velocity and area.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In flowing water, pressure drops, while speed up tops; height's the key, it's energy's plea!
📖 Fascinating Stories
-
Imagine you're watering a garden. As you push the hose nozzle, the water speed increases, making it spray further while pressure at the nozzle decreases, illustrating Bernoulli’s principle.
🧠 Other Memory Gems
-
Remember 'BVP' for Bernoulli's variables: Pressure, Velocity, and Height.
🎯 Super Acronyms
Use 'PEV' for Bernoulli — P for Pressure, E for Energy, V for Velocity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dimensional Homogeneity
Definition:
The property of an equation where all its terms have the same dimensions.
-
Term: Bernoulli's Equation
Definition:
An equation representing the conservation of energy in flowing fluids that relates pressure, velocity, and height.
-
Term: Pressure (P)
Definition:
The force exerted by a fluid per unit area.
-
Term: Velocity (v)
Definition:
The speed of flow in a given direction.
-
Term: Height (h)
Definition:
Refers to the elevation in a fluid context, usually measured from a reference point.
-
Term: Density (ρ)
Definition:
The mass of the fluid per unit volume.
-
Term: Kinetic Energy (KE)
Definition:
The energy an object possesses due to its motion, calculated as 0.5 * mass * velocity squared.