Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Kinematic Similarity
Unlock Audio Lesson
Today, we will delve into kinematic similarity. Can anyone tell me what they think it means?
Is it about how model movements replicate those of real prototypes?
Exactly! Kinematic similarity ensures that the velocity and streamline patterns of a model are the same as they are in the prototype. This is essential for accurate predictions in fluid behavior.
How do we measure kinematic similarity?
Great question! We measure it using concepts like the Reynolds number. Remember, the formula for it is Re = inertial forces / viscous forces. Let's keep that in mind!
So, if the Reynolds number is the same in both model and prototype, does that mean they are similar?
Yes, if they match, we can say that the kinematic characteristics are properly scaled. This is crucial for experiments in fluid mechanics.
To summarize, kinematic similarity allows us to ensure that the modeling effectively simulates the prototype conditions, using principles such as the Reynolds number to establish those relationships.
Relevance of Kinematic Similarity
Unlock Audio Lesson
Now let's talk about why achieving kinematic similarity is critical in experiments. Can anyone think of a scenario where this might be necessary?
In designing dams and bridges, we need to know how water flows.
Exactly! When we scale down models of these structures, we use kinematic similarity to ensure the flow patterns we observe in our tests can accurately predict the behavior of the real-world prototypes.
Do we only look at the Reynolds number for similarity?
Good question! We also consider the Froude number in free surface flows. It's all about matching the patterns of movement between model and prototype.
How do we apply this in real experiments?
By ensuring that both the velocities and time scales are preserved, we can replicate the real-world conditions effectively.
To recap, kinematic similarity is vital for accurate modeling, and we use parameters like Reynolds and Froude numbers to ensure these conditions are met.
Applications of Kinematic Similarity
Unlock Audio Lesson
Let's further explore the applications of kinematic similarity. Can anyone suggest how we can utilize this concept?
In simulations of flood scenarios?
Absolutely! In simulations like these, achieving kinematic similarity helps predict how water will interact with structures and landscapes accurately.
What about in vehicle aerodynamics?
Exactly right. Kinematic similarity allows us to understand how fluid flows around a vehicle's shape, which is critical for reducing drag.
So kinematic similarity has a wide range of engineering applications!
You got it! It plays a crucial role across various fields from civil engineering to automotive industries.
In summary, kinematic similarity is applied in multiple scenarios, ensuring fluid dynamics in experiments closely mirror real-world conditions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Kinematic similarity plays a crucial role in fluid mechanics by ensuring that the kinematic parameters of model scale experiments resemble those of the prototype. This section covers the significance of kinematic similarity, its basic principles, and how it can be applied in modeling situations.
Detailed
Kinematic Similarity in Fluid Dynamics
In fluid mechanics, kinematic similarity is essential for ensuring that models accurately represent the behavior of prototypes. This involves creating an equivalency between the velocities and streamline patterns of a model and its respective prototype. Kinematic similarity can be achieved through specific scaling methods involving the Reynolds number, Froude number, or Mach number, which allow for a direct relationship between model and prototype flow conditions. The section emphasizes the necessity of maintaining kinematic similarity, especially in experiments where replicating fluid behavior in scaled-down models is vital for accurate analysis and design.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Kinematic Similarity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
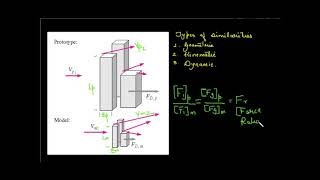
Kinematic similarity refers to the condition where models and prototypes share the same velocity patterns and streamline characteristics, such that homologous points in the model and prototype correspond to the same time and position.
Detailed Explanation
Kinematic similarity is defined as the condition where motion patterns of a model and a prototype are similar at corresponding points. This implies that the velocity of flowing fluids in both the model and the prototype should be proportional at corresponding locations, ensuring that the same flow phenomena occur under similar operational conditions. Therefore, it involves ensuring that the streamlines—the paths followed by fluid particles—are consistent in both the model and prototype. When conducting experiments, achieving kinematic similarity ensures reliable predictions of fluid behavior.
Examples & Analogies
Imagine a group of children playing with toy boats in a tub filled with water. If one child uses a miniature boat that moves with similar patterns to a larger boat moving in a lake, we can observe how the toy boat mimics the larger one. If the currents and forces acting on the toy are similar to those on the real boat, even though they are of different sizes, we can say there is a kinematic similarity, making it easier to predict how both will perform under various situations.
Parameters for Achieving Kinematic Similarity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To achieve kinematic similarity, dimensions such as Reynolds number, Froude number, and Mach number can be utilized, as they relate to flow characteristics and conditions in both models and prototypes.
Detailed Explanation
Kinematic similarity is quantified using dimensionless numbers such as Reynolds number, Froude number, and Mach number. The Reynolds number relates to the ratio of inertial forces to viscous forces, impacting whether the flow is laminar or turbulent. The Froude number relates the flow's inertia to the gravitational force, particularly important in free surfaces like rivers or lakes. The Mach number compares the speed of the flow to the speed of sound in the medium, pertinent to compressible flows. By ensuring that these dimensionless parameters are equal for both the model and the prototype, you can maintain similarities in fluid behavior.
Examples & Analogies
Consider a small model airplane. To ensure it performs similarly to a real airplane, the design must account for various factors like speed and flow over its wings. Engineers replicate conditions using scales of measurement (like the speed of air over the wings) that correspond to real flight conditions. By maintaining similar Reynolds and Froude numbers in both models, the small model can predict how the actual airplane will behave during flight.
Implications of Kinematic Similarity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Kinematic similarity allows the experiments conducted in smaller models to accurately predict the behavior of much larger prototypes, thereby enhancing the design and analysis of engineering projects.
Detailed Explanation
The application of kinematic similarity in modeling allows engineers to confidently translate findings obtained from small-scale experiments to larger, full-scale prototypes. By ensuring that both the model and the prototype maintain the same flow characteristics, even with different sizes, it enables more efficient testing and reduces the risk and cost of full-scale model implementation. Essentially, it provides a method to validate hypotheses in a controlled environment before applying them to real-world applications.
Examples & Analogies
Think about how architects use scale models to showcase new buildings. They create small representations that can be easily manipulated and viewed from all angles. By observing how wind movements affect the small model, architects can understand how wind will interact with the actual building. This predictive capability ensures that designs are not only practical but also safe and responsive to environmental factors, much like ensuring that water flow behaves consistently in both small and large-scale river models.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Kinematic Similarity: The concept that ensures model movements replicate those of the prototype, particularly relevant in fluid dynamics.
-
Reynolds Number: A key parameter used to determine flow regimes, essential for establishing kinematic similarity.
-
Froude Number: A critical dimensionless number that also plays a significant role in analyzing fluid flows, particularly in free surface situations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In modeling dam overflow scenarios, maintaining kinematic similarity is crucial to accurately predict flood behavior.
-
Automotive wind tunnel tests utilize kinematic similarity to comprehend how airflow behaves around vehicle shapes.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In models so small, let’s keep track, with Reynolds numbers we never look back!
📖 Fascinating Stories
-
Imagine a tiny dam model built to mirror a giant one. If the tiny dam's water flows just like reality, you've got kinematic similarity down!
🧠 Other Memory Gems
-
Remember 'KRF' - Kinematic, Reynolds, Froude to maintain flow behavior!
🎯 Super Acronyms
KSM
- Kinematic Similarity Matters!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Kinematic Similarity
Definition:
A principle in fluid dynamics ensuring that the velocities and streamline patterns of a model correspond with those of its prototype.
-
Term: Reynolds Number
Definition:
A dimensionless number proportionate to inertial forces divided by viscous forces in a fluid, indicating flow characteristics like laminar or turbulent.
-
Term: Froude Number
Definition:
A dimensionless number used in analyzing fluid flow, which is the ratio of inertial forces to gravitational forces.