Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Dimension Analysis
Unlock Audio Lesson
Welcome, everyone! Today we'll discuss dimension analysis. Can anyone tell me what dimension analysis involves?
Is it about understanding different physical quantities like length and weight?
Exactly, Student_1! Dimension analysis helps us understand how various quantities relate to one another, especially in fluid mechanics. For instance, we categorize dimensions into length, area, volume, velocity, and pressure.
Can you give us an example of how this is applied?
Certainly! For example, when studying a river like the Brahmaputra, we consider physical dimensions in our modeling—like scaling down a river's width to mimic flow behavior in a lab setting. This leads us into geometric similarity.
What's geometric similarity?
Great question, Student_3! Geometric similarity ensures our model dimensions are scaled down correctly while maintaining proportionate shapes.
Why is that important?
Maintaining geometric similarity allows us to accurately predict how real-world systems will behave. Remember the acronym 'G-SIM' for Geometric Similarity!
Understanding Kinematic Similarity
Unlock Audio Lesson
Now, let’s discuss kinematic similarity. Can anyone suggest what this might mean?
Is it related to how things move?
Yes, it involves the relationship between velocities of different scales! When we achieve kinematic similarity, model and prototype velocities correspondally match in factors.
Do we use factors like Reynolds number for this?
Indeed, Student_1! Reynolds number helps us ensure the flow patterns between the model and prototype remain similar, which is vital for accuracy.
Can you give an example of where this applies?
Sure! In dam modeling, we relate model wave heights to prototype wave heights through flow conditions, utilizing a matching Froude number!
That sounds complex!
It can be, but remember the phrase 'Kinematic Consistency Keeps Flow Precise' to recall its importance. Any other questions?
Exploring Dynamic Similarity
Unlock Audio Lesson
Let's move on to dynamic similarity. Who can explain what’s significant about it?
Does it have something to do with forces?
Exactly! Dynamic similarity captures how all forces—pressure, gravity, and inertia—act similarly in both model and prototype.
How do we ensure these forces are balanced?
By maintaining geometric and kinematic similarity first! Once we achieve those, dynamic similarity follows naturally.
Can you explain how forces are expressed?
Certainly! We equate the forces acting on both systems. For example, the pressure force of the model must match that of the prototype in ratio and vector direction.
That makes more sense now!
Great! Just remember 'Dynamic Consistency Drives Design' when thinking about forces in similarity.
Dimensional Analysis and Equation Validation
Unlock Audio Lesson
Finally, let’s tie everything together by discussing dimensional analysis for verifying equations. What’s the benefit of ensuring dimensional homogeneity?
Is it to avoid mistakes in calculations?
Exactly, Student_4! By confirming each term in an equation has the same dimensions, we can verify that the equations we use in fluid mechanics are correct.
Can you illustrate that with an example?
Sure! Let's consider Bernoulli's equation. Each term must have dimensions of energy per unit weight, which indicates consistency across the equation.
What if they don’t match?
Good question! If dimensions don’t match, that signals potential errors in the derivation of the equation.
It’s fascinating how everything links back to those fundamental dimensions!
Absolutely! Remember, 'Dimensional Analysis Validates Solutions' as a key take-home point.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Dimension analysis and similarity are foundational concepts in fluid mechanics essential for validating models and prototypes. This section elaborates on geometric, kinematic, and dynamic similarities, illustrating their application in real-world scenarios. Furthermore, it emphasizes the use of dimension analysis to ensure the correctness of derived equations, particularly in complex fluid dynamics.
Detailed
Dimension Analysis and Similarity
In fluid mechanics, the concepts of dimension analysis and similarity are crucial for conducting experiments, particularly physical modeling. The section begins by defining the dimensions of fluid mechanics properties, categorizing them into basic geometry, velocity, pressure, and other essential terms.
The significance of physical modeling is highlighted using examples like the Brahmaputra River and various dam projects, where prototype dimensions must be scaled down for testing in controlled environments. The concepts of geometric similarity, kinematic similarity, and dynamic similarity are explained, underscoring their necessity for creating accurate models.
Moreover, the section delves into dimensional analysis, particularly concerning Bernoulli’s equation, to validate the derived equations’ correctness. Various examples and detailed explanations of Reynolds number experiments illustrate the transition between laminar, transitional, and turbulent flows. The practical implications of these principles in the engineering and design process are emphasized, further framing the discussion in the context of real-world scenarios and large-scale engineering projects.
Youtube Videos
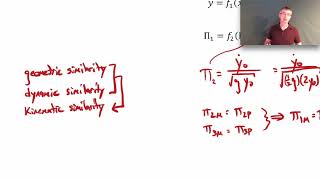
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Dimension Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Welcome all of you for this lectures on fluid mechanics and today we will discuss about dimension analysis and the similarity. I have been following these 3 reference books, but the mostly today I will talk about the professor Radhakrishnan’s books, which is one of the (()) on the dimension analysis and the similarity concept.
Detailed Explanation
This chunk introduces the topic of dimension analysis and similarity in fluid mechanics. Dimension analysis involves studying the relationships between different physical quantities by expressing them in terms of their fundamental dimensions (like length, mass, time). This approach helps simplify complex problems and facilitate understanding of the principles that govern fluid behavior. The mention of Professor Radhakrishnan’s books indicates that this lecture will draw heavily on established concepts in the field.
Examples & Analogies
Think of dimension analysis like reading a recipe that requires specific measurements for different ingredients. Just as following the right measurements leads to a delicious cake, applying the correct dimensions and relationships in physics leads to accurate predictions in fluid dynamics.
Physical Modelling Experiments
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
I will start with the physical modelling experiments, what we have in IIT Guwahati or elsewhere, how we conduct the physical modelling experiment. Then I will talk about the dimensions of fluid mechanics properties which last class we discussed, but just I have to repeat it and more interesting things today I will talk about the dimensional analysis of Bernoulli's equation.
Detailed Explanation
This chunk emphasizes the importance of physical modeling in understanding fluid mechanics. Physical modeling experiments involve creating scaled-down models of real-world systems (like rivers or dams) to study how they behave under various conditions. This method allows researchers to observe phenomena that can be difficult or impossible to measure directly in large-scale prototypes. The reference to Bernoulli's equation suggests that the session will explore specific applications of dimensional analysis within fluid dynamics.
Examples & Analogies
Imagine trying to understand how a large river flows. Instead of studying the entire river directly, you create a small model in a lab. Watching how water flows through this model helps you predict how the actual river will behave, much like a child learning to ride a bike with training wheels before trying to ride a full-sized bicycle.
Prototype versus Model Dimensions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The dimensions of real rivers and we call the dimensions of prototype. So the real river dimensions what is that is given as a prototype dimensions, that is what we reflect in the modelling setups what we have, where we scale down it with the distance level as well as the geometry level.
Detailed Explanation
This segment explains the difference between prototype dimensions (the actual measurements of a system) and model dimensions (scaled-down versions). Scaling is crucial in physical modeling as it allows engineers to create manageable experiments while still obtaining valid results. For example, if a river is 6 kilometers long, a model might be scaled down to 1.73 meters to facilitate testing in a lab. This proportional representation helps maintain the relationships between different characteristics of the flow.
Examples & Analogies
Scaling down is like creating a miniature version of a city to plan out a new development. Architects use small models to visualize how buildings and roads interact without needing to build the entire project first.
Importance of Similarities
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us look at the concept of similarity or similitude, solved examples and summary. But these type of experimental set up we conduct before implementing major projects like barrage, the dam projects, the port projects, all the major project before implementing it these all we tested.
Detailed Explanation
This chunk introduces the concept of similarity or similitude, which is essential in ensuring that the behaviors observed in scaled models accurately reflect those in real-life prototypes. By establishing geometric, kinematic, and dynamic similarities, researchers can apply findings from small-scale models to large-scale structures. This testing phase is critical in avoiding costly mistakes in real-world projects like dams or ports, ensuring they function effectively when built.
Examples & Analogies
Consider how a software prototype is tested before final release. Developers use small-scale models to identify bugs and improve user experience before launching the full software, much like engineers test scaled-down models before building a large dam.
Geometric, Kinematic, and Dynamic Similarity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
that is what is the geometric similarity, kinematic similarity, dynamic similarity and the thermal similarity. So as we are not talking about energy, conservations much more in these lectures, we focus on these 3 similarity, geometry, kinematics and the dynamic similarity.
Detailed Explanation
This section outlines three main types of similarity relevant in fluid dynamics: geometric similarity (ensuring the model has the same shape proportions), kinematic similarity (ensuring the motion patterns of fluid flow in the model match those of the prototype), and dynamic similarity (ensuring the forces acting on the fluid in the model mimic those in the prototype). These similarities are crucial for ensuring that models yield reliable data that can be generalized to larger systems.
Examples & Analogies
Think of a puppet show. The puppets (model) need to move like the actual people (prototype) to convey the right story. Geometric similarity makes sure they look similar, kinematic similarity ensures they move similarly, and dynamic similarity ensures audience reaction is the same whether watching the puppets or real actors.
Conclusion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So looking at the part, the first I am talking about geometric similarity. If you look it, this is what the prototypes, pole scale okay, that is what is the Boeing X48B but we cannot conduct this big scale experiments, what we do it we scale down it.
Detailed Explanation
The conclusion emphasizes the practical aspects of realization in fluid mechanics through scaling and similarity. It reveals how detailed studies of prototypes using scaled models lead to successful designs in fields like aerospace. The example of the Boeing model illustrates that while full-scale tests are not always feasible, scaled tests provide essential data needed for decision-making.
Examples & Analogies
When training for a race, athletes often practice using scaled-down versions of their equipment to improve their skills. This practice helps them prepare effectively without needing to always use the actual racing gear.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dimension Analysis: A method to verify the consistency of equations and relationships in physics.
-
Geometric Similarity: Ensures the model replicates the proportions of the prototype in every aspect.
-
Kinematic Similarity: Involves matching velocity and flow patterns between the model and prototype.
-
Dynamic Similarity: Requires that all forces remain proportionately similar in both model and prototype.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The scaling of a laboratory model of the Brahmaputra River to mimic its flow characteristics while maintaining geometric proportions.
-
Utilizing Reynolds number to differentiate between laminar and turbulent flows in models versus real prototypes.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
AT G-SIM we learn to scale, Dimensions in models never fail!
📖 Fascinating Stories
-
Imagine a small stream mimicking a mighty river—just as the small model flows with grace and precision, so does the grand river, showcasing geometric shapes and perfect flow.
🧠 Other Memory Gems
-
Use 'GK-D' to remember: G for Geometric similarity, K for Kinematic similarity, and D for Dynamic similarity.
🎯 Super Acronyms
Remember 'SPEED' for the conditions of similarity
- Scaling
- Proportionality
- Equivalence
- Energy
- Dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dimension Analysis
Definition:
A method to check the consistency of physical quantities by examining their dimensions.
-
Term: Geometric Similarity
Definition:
A condition where the geometric shapes of the model are proportional to those of the prototype.
-
Term: Kinematic Similarity
Definition:
A condition where the patterns of motion and velocities of the model replicate those of the prototype.
-
Term: Dynamic Similarity
Definition:
A condition where the forces affecting the model and prototype are proportional and act in similar manners.
-
Term: Bernoulli's Equation
Definition:
An equation that relates the pressure, velocity, and elevation in a moving fluid.