Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Head Loss
Unlock Audio Lesson
Today we are going to explore major and minor head losses in fluid systems. Can anyone tell me what we mean by major head losses?
Major head losses are those caused by friction in the pipes, right?
Exactly! Major head losses are primarily due to friction along the length of the pipe. Now, what about minor losses?
Minor losses are due to things like bends, valves, and fittings in the system?
Correct! Minor losses occur at transitions in the pipe structure. Remember our acronym MVB for Minor Losses: Minor, Valve, Bend. Can anyone give an example of a minor loss component?
A valve loss, like when water passes through a valve.
Well done! Understanding both major and minor losses is crucial for designing efficient piping systems.
Applying Bernoulli's Equation
Unlock Audio Lesson
Now, let’s apply Bernoulli’s equation. Can anyone remind me what Bernoulli’s equation relates in fluid flow?
It relates pressure, velocity, and elevation head in a flowing fluid.
Good recall! For our GATE problem, we need to calculate the pressure drop. If we know the elevation difference between reservoirs, how would we proceed?
We’ll substitute the head loss values and the friction factor into the equation.
Exactly! By knowing the elevation loss and the friction factor, we can solve for pressure values at different points in the system.
And then we can determine the discharge to reservoir C!
Exactly right! Let's practice these calculations together step by step.
Example Problem Walkthrough
Unlock Audio Lesson
Let’s walk through an example similar to the one from GATE 2015. We have a pipe with a 30-meter elevation difference. What information do we need to solve for the discharge?
We’ll need the length of the pipe, the friction factor, and the diameter.
Correct! We also need the values for head loss due to friction. How do we calculate the total head loss?
Using the Darcy-Weisbach equation, I think!
Right! Now, let's plug in the values to find out the discharge into reservoir C when we have calculated the total head losses.
This helps clarify how friction can impact flow in a real system!
Exactly! It reflects the importance of accounting for all losses in practical applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we analyze head losses in a pipe connecting two reservoirs and a branch to a third reservoir, emphasizing the application of Bernoulli's equation. Detailed calculations involve friction factors, energy losses, and showcase problems similar to those found in the GATE 2015 exam.
Detailed
In this section, we discuss head losses in piping systems, focusing on both major losses (due to friction) and minor losses (caused by fittings and valves). The section includes a practical problem from the GATE 2015 exam, where a pipe connecting two reservoirs is analyzed for fluid discharge into a third reservoir. Key calculations leverage Bernoulli's equation and the Darcy-Weisbach Equation for head loss. We navigate through concepts of pressure calculations, friction factors, and different loss coefficients. The significance of energy gradients and hydraulic principles is emphasized throughout the problem-solving process.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Head Loss in Pipes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So that means I know the head losses that is what is computed here by substituting this value. There will be minor losses like bend losses, valve losses, the entry and exit losses all the components, this entry and exit loss we do not consider it here only the bend loss and valve loss we compute it which we have these values.
Detailed Explanation
In fluid mechanics, 'head loss' refers to the loss of pressure that occurs due to friction and other factors as fluid travels through a pipe. In this section, it mentions both major and minor losses. Major losses are primarily due to friction in the pipe, often computed using the Darcy-Weisbach equation. Minor losses, on the other hand, occur at fittings like bends, valves, and other transitions in the system. For this problem, only bend losses and valve losses are computed, while entry and exit losses are assumed negligible.
Examples & Analogies
Think of head loss as the energy spent in a game of tug-of-war. If everyone is pulling hard but there are obstacles (like mud or hills, which represent bends and valves), it becomes harder to move forward, just like the fluid losing pressure due to obstacles in a pipe.
Major Pipe Head Loss Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Major pipe head loss (due to friction): [Equation] Minor losses: [Equation].
Detailed Explanation
This section presents how to calculate major pipe head loss using equations explicitly related to the friction factor and other properties of the fluid flow. It emphasizes using specific equations to find head loss due to friction, which is crucial for engineers to predict how much energy will be lost in real systems due to factors like pipe roughness and flow velocity.
Examples & Analogies
Imagine sliding down a slide. If the slide is smooth, you go down fast; but if it's rough, you slow down. The friction in the pipe is like the rough slide, causing water to lose energy (or head).
Applying Bernoulli’s Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we are substituting Bernoulli’s equations, the modified Bernoulli’s equations to compute what could be the pressure.
Detailed Explanation
Bernoulli's equation relates pressure, velocity, and height in fluid flows. In this case, after calculating the head losses, Bernoulli’s equation is used to calculate the resultant pressure at a specific point in the system. This approach employs the modified form of the equation to account for the losses incurred.
Examples & Analogies
Think of Bernoulli’s equation as a balance scale between pressure and speed. If the water speeds up through a section (like a narrow part of a river), its pressure will drop, like how you feel when you dart through a crowd; you're moving fast but might feel lighter as you push through.
Problem Description
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
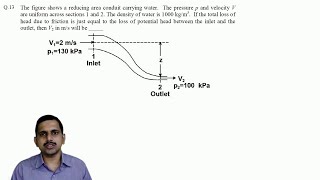
Now you take it the second problems which has the GATE 2015 problems is that the pipe of 0.7 meter diameter has a length of 6 kilometer connects the two reservoirs okay and the water level in the reservoirs is 30 meter above the water level of reservoir B.
Detailed Explanation
This describes a specific problem from the GATE exam, where a pipe connects two reservoirs with significant elevation difference. The length and diameter of the pipe are specified, and knowing these parameters helps in calculating the head loss and ultimately the flow rate into reservoir C.
Examples & Analogies
Think of the reservoirs as two swimming pools at different heights. To get water from the higher pool to the lower one through a long pipe, you have to account for gravity pulling it down and the resistance the pipe offers, much like trying to pour water down a long, narrow funnel – the height and length matter!
Discharge Calculation and Energy Loss
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Considering this accelerations due to the gravity this value neglecting the minor loss the discharge into reservoir is what, okay?
Detailed Explanation
This section hints at the need to calculate the discharge rate of water flowing into the third reservoir C while neglecting minor losses. The significant point here is that the total head losses from the energy due to the height difference will dictate how much water can flow into the reservoir efficiently.
Examples & Analogies
Visualize a water slide that starts high and ends low. How fast the kids can go down does depend on how high the slide starts and how much friction there is on the slide. Similarly, the energy lost in overcoming gravity affects how much water can flow into reservoir C.
Substituting Values to Find Discharge
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at these problems is exactly for the problems what we discussed it, nothing else, okay. Here we have a major losses and minor losses.
Detailed Explanation
This part reiterates that to solve the problems presented, one must carefully substitute known values into the equations derived for major and minor losses. Understanding each component of the system is essential for accurately calculating discharge and other parameters of interest.
Examples & Analogies
Imagine baking a cake: if you have all your ingredients and exact measurements, you can calculate how much batter you’ll get. Similarly, correctly putting in values for flow rates and losses helps you find out how much water will flow through the system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Major Head Loss: Loss due to friction.
-
Minor Head Loss: Loss due to fittings and components.
-
Bernoulli’s Equation: Relates pressure and energy in fluids.
-
Darcy-Weisbach Equation: Calculates head loss in pipes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using the Darcy-Weisbach Equation to find the head loss over a long stretch of pipe.
-
Calculating the pressure drop between two reservoirs considering friction and elevation changes.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When water flows like a stream, friction losses make it a dream, but bends and valves can cause a scream!
📖 Fascinating Stories
-
Imagine water flowing smoothly from reservoir A to B. However, when it encounters a bend, it slows down, losing energy—a lesson in head loss!
🧠 Other Memory Gems
-
MVB for minor losses: Minor, Valve, Bend.
🎯 Super Acronyms
HLM for Head Loss Management
- Head
- Loss
- Management.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Major Head Loss
Definition:
Loss of energy due to friction along the length of a pipe.
-
Term: Minor Head Loss
Definition:
Loss of energy due to components like valves and bends in a piping system.
-
Term: Bernoulli's Equation
Definition:
A principle that relates pressure, velocity, and height in a flowing fluid.
-
Term: DarcyWeisbach Equation
Definition:
An equation used to calculate head loss due to friction in a pipe.
-
Term: Friction Factor
Definition:
A dimensionless number used to calculate pressure loss in a pipe due to friction.