Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Laminar Flow
Unlock Audio Lesson
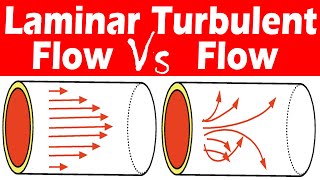
Let's start with laminar flow. It is characterized by smooth, parallel layers of fluid flowing with minimal mixing. This typically occurs at low velocities and low Reynolds numbers, generally below 2300.
What happens at low Reynolds numbers that makes the flow laminar?
Great question! At low Reynolds numbers, viscous forces dominate over inertial forces, allowing the fluid to flow in a stable and orderly manner.
Can you give me an example of laminar flow in real life?
Sure! A good example is the flow of oil in a thin pipe or a slow-moving stream where the fluid flows in layers.
How do we visualize laminar flow with virtual fluid balls?
If we imagine each layer as a virtual ball, they slide smoothly over one another. This visualization helps us understand the orderly motion in laminar flow.
"### Summary
Turbulent Flow Characteristics
Unlock Audio Lesson
Now let's talk about turbulent flow. Unlike laminar flow, turbulent flow exhibits chaotic and irregular movements, commonly occurring at high Reynolds numbers—typically over 4000.
What triggers this chaotic behavior in fluid?
When the inertia forces significantly exceed the viscous forces, this instigates chaotic movements, leading to the turbulence we observe.
Can you illustrate how turbulent flow looks using the virtual fluid ball concept?
Absolutely! In turbulent flow, our virtual balls break apart, creating smaller balls that move unpredictably, resulting in complex mixing and energy dissipation.
Why is it important to understand the transition from laminar to turbulent flow?
Understanding this transition is crucial for designing efficient fluid transport systems, as the flow type affects energy and momentum transfer.
"### Summary
Reynolds Number and its Significance
Unlock Audio Lesson
Next, let's discuss the Reynolds number, which is vital for determining the flow regime. It is defined as the ratio of inertial forces to viscous forces in a fluid.
How is the Reynolds number calculated?
The formula is Re = (ρVD)/μ, where ρ is the density, V is the average velocity, D is the characteristic length or diameter of the pipe, and μ is the dynamic viscosity.
What does a high Reynolds number indicate about the fluid behavior?
A high Reynolds number indicates turbulent flow, signifying a dominance of inertial forces which leads to chaotic fluid behavior.
Are there specific applications that rely on controlling flow regimes?
Yes! In engineering, controlling the flow regime is crucial for optimizing systems like pipelines and HVAC systems to ensure efficiency.
"### Summary
Practical Implications of Flow Types
Unlock Audio Lesson
Finally, let’s explore the practical implications of understanding laminar and turbulent flows in various engineering applications.
How do these flow types affect pipeline design?
Excellent question! Engineers must consider flow characteristics to minimize losses; laminar flow allows for efficient transport, while turbulent flow may lead to energy loss and higher pressure drops.
What strategies can we use to manage turbulent flow?
Strategies include resizing pipes, introducing turbulence-reducing fittings, and designing systems to maintain laminar flow where desired.
Why is visualizing these flows important?
Visualization helps understand and predict flow patterns, essential for optimizing and troubleshooting fluid systems.
"### Summary
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the differences between laminar and turbulent flows by defining both types, explaining the significance of the Reynolds number, and detailing how fluid behavior changes with varying flow conditions. It also introduces the concept of virtual fluid balls to illustrate the dynamics of these flows.
Detailed
Detailed Summary
In this section, we delve into the crucial differences between laminar and turbulent flows in fluid mechanics. Laminar flow is characterized by smooth, orderly layers of fluid moving in parallel, where the viscous forces dominate and there’s a low Reynolds number (typically below 2300). In contrast, turbulent flow involves chaotic and irregular fluid movements, where inertia forces surpass viscosity and the Reynolds number exceeds 4000. The transition between these two states occurs in an intermediate range, typically between Reynolds numbers of 2300 and 4000, where flow can become unstable.
To simplify the understanding of these flow types, we employ the concept of virtual fluid balls, which helps visualize how fluids behave under varying conditions. In laminar flow, these balls represent structured layers; as the flow becomes turbulent, the balls disintegrate into smaller units, leading to chaotic mixing and momentum transfer. The significance of these distinctions is not only theoretical but practical, as they are fundamental in designing efficient pipe systems in engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Flow Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Laminar flow is characterized by smooth, orderly layers of fluid that slide past one another, while turbulent flow is marked by chaotic and irregular movements. Laminar flow occurs at lower velocities and lower Reynolds numbers, whereas turbulent flow appears at higher velocities and higher Reynolds numbers.
Detailed Explanation
In fluid mechanics, there are two primary types of flow: laminar and turbulent. In laminar flow, fluid moves in parallel layers with minimal disruption between them, leading to smooth motion and predictable behavior. This kind of flow occurs at low individual particle speeds and typically has a Reynolds number below 2300. On the other hand, turbulent flow is characterized by chaotic and irregular fluid movements, resulting in eddies and swirls which enhance mixing. Turbulent flow generally occurs at higher velocities and has a Reynolds number above 4000.
Examples & Analogies
Imagine a calm river on a clear day where the water flows smoothly and steadily - this is akin to laminar flow. Now picture a fast-moving river during a storm where waves crash and foam forms - that's a representation of turbulent flow.
Reynolds Number and Flow Transition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Reynolds number, a dimensionless quantity, determines the type of flow in a fluid. It is the ratio of inertial forces to viscous forces. A Reynolds number below 2300 indicates laminar flow, between 2300 and 4000 suggests transition flow, and above 4000 indicates turbulent flow.
Detailed Explanation
The Reynolds number (Re) plays a crucial role in determining whether a flow is laminar, transitional, or turbulent. It is calculated using the formula Re = (ρVD)/μ, where ρ is the fluid density, V is the flow velocity, D is the pipe diameter, and μ is the dynamic viscosity. When the Reynolds number is less than 2300, the flow is laminar - smooth and orderly. Between 2300 and 4000, the flow is in a transition phase, where it may fluctuate between laminar and turbulent characteristics. Once the Reynolds number exceeds 4000, the flow becomes turbulent, resulting in chaotic behavior.
Examples & Analogies
Think of a garden hose: when you gently turn on the water (low velocity), the water flows smoothly (laminar). But if you fully open the tap, the water rushes out in a wild splatter (turbulent) as it increases in velocity.
Characteristics of Laminar Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In laminar flow, fluid particles move in smooth layers or streamlines. The flow is stable, and there are minimal fluctuations. The viscosity of the fluid plays a significant role in ensuring that layers do not mix much.
Detailed Explanation
Laminar flow is characterized by orderly and predictable streamlines, with adjacent layers of fluid moving past each other without significant mixing or turbulence. The forces acting on the fluid are predominantly viscous, meaning that the internal resistance to flow is sufficient to keep the smooth layers intact. In this regime, because the flow patterns are stable, calculations for laminar flow are more straightforward and predictable.
Examples & Analogies
Picture a group of dancers performing a perfectly synchronized routine - such cohesive movement represents laminar flow, where every dancer (fluid layer) is moving in harmony without disruption.
Characteristics of Turbulent Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Turbulent flow is characterized by irregular, chaotic fluid motion, large velocity fluctuations, and mixing of different fluid layers. This type of flow leads to increased energy dissipation and is generally associated with higher velocities.
Detailed Explanation
In contrast to laminar flow, turbulent flow is marked by erratic fluctuations and swirling motions within the fluid, leading to a high degree of mixing across different layers. This chaotic nature results in enhanced energy loss due to friction and makes it necessary to employ complex models to predict fluid behavior accurately. Turbulent flow is more common in practical applications, especially in situations with high flow rates or larger diameters.
Examples & Analogies
Imagine a crowded dance floor where everyone is moving in different directions, bumping into one another and changing positions quickly. This chaotic environment represents turbulent flow, showcasing how the movements of individuals (fluid particles) create a complex and unpredictable pattern.
Transition Between Laminar and Turbulent Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The transition from laminar to turbulent flow is not abrupt. As flow speed increases, flow may experience fluctuations, indicating the transition phase. In this condition, flows may not be clearly categorized as either laminar or turbulent.
Detailed Explanation
When flow conditions change, such as increasing velocity, the transition from laminar to turbulent flow does not happen all at once but occurs over a range where the flow becomes unstable. This transitional phase can involve isolated pockets of turbulence interspersed with regions of laminar flow, making it difficult to classify the overall flow regime clearly.
Examples & Analogies
Consider mixing two distinct colored paints where initially they stay separate (laminar), but as you stir them faster, you see swirling patterns forming - this is the transition before they become fully mixed (turbulent) where the colors blend unpredictably.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Laminar Flow: Flow characterized by orderly layers and low Reynolds numbers.
-
Turbulent Flow: Chaotic fluid motion occurring at high Reynolds numbers.
-
Reynolds Number: Ratio of inertial forces to viscous forces, crucial for predicting flow type.
-
Virtual Fluid Balls: Conceptual tool for visualizing fluid behavior.
-
Transition Point: The Reynolds number range between laminar and turbulent flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Flow of honey in a thin pipe is an example of laminar flow due to its viscosity and slow speed.
-
Whitewater rapids demonstrate turbulent flow, characterized by chaotic movement and mixing of water.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In laminar flow, layers glide, while turbulence is hard to hide.
📖 Fascinating Stories
-
Imagine two rivers. One flows calmly with layers gliding smoothly, another whirls chaotically with splashes everywhere; that's laminar and turbulent flow!
🧠 Other Memory Gems
-
RAT - Remember: All Turbulent flows are chaotic, Representing high Reynolds numbers.
🎯 Super Acronyms
LHT - Laminar Has tranquility, Turbulent Has chaos.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Laminar Flow
Definition:
A type of fluid flow characterized by smooth and orderly layers moving parallel to one another.
-
Term: Turbulent Flow
Definition:
A type of fluid flow characterized by chaotic and irregular movements, typically occurring at high velocities.
-
Term: Reynolds Number
Definition:
A dimensionless number used to predict flow regimes, defined as the ratio of inertial forces to viscous forces in fluid flow.
-
Term: Virtual Fluid Balls
Definition:
An illustrative concept used to visualize fluid flow, representing the fluid as individual balls to better understand motion and behavior.
-
Term: Critical Reynolds Number
Definition:
The specific value of Reynolds number that marks the transition between laminar flow and turbulent flow.