Mass and Momentum Flux Components
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Virtual Fluid Balls
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll start discussing the concept of virtual fluid balls. Imagine we have balls of various sizes and colors representing different fluids. Can anyone tell me how these balls might behave when they encounter turbulence?

I think they might break apart into smaller balls if the turbulence is strong!

Exactly! When turbulence increases, these fluid balls can disintegrate, allowing smaller balls to transfer mass and momentum differently. That's central to understanding flux in turbulent flows.

What happens if the turbulence decreases?

Good question! With reduced turbulence, some of these smaller balls can re-integrate. This dynamic interaction is crucial for understanding energy efficiency in fluid transport.
Characteristics of Laminar Flow vs Turbulent Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's dive deeper into the differences between laminar and turbulent flows. In laminar flow, fluid flows in smooth layers. When we use our virtual balls analogy, how do you think the balls behave in laminar flow?

I think they would move in organized layers without breaking apart.

Correct! In laminar flow, there's minimal interaction between layers, and the virtual balls move smoothly. Now, when we shift to turbulence, what changes?

The balls would start to disintegrate and mix with each other.

Precisely! This mixing results in complex flow patterns that lead to energy dissipation and fluctuations in velocity. These effects are crucial for fluid dynamics.
Understanding Reynolds Number
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's talk about the Reynolds number, which is essential for characterizing flow regimes. It indicates whether a flow is laminar, transitional, or turbulent. Does anyone remember the thresholds?

Isn't laminar flow characterized by a Reynolds number below 2300?

Exactly! Below 2300, the flow is laminar. What about the transitional phase?

That’s between 2300 and 4000, right?

Yes! Once it crosses 4000, the flow becomes turbulent. Understanding these thresholds helps engineers optimize fluid systems.
Fluctuating Velocity Components
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's examine fluctuating velocity components in turbulent flow. How do these fluctuations impact mass and momentum flux?

The fluctuations would cause variations in mass transport across different layers.

Very good! Fluctuations do create additional mass fluxes because they can either introduce or remove mass from sections of flow. How could that affect momentum?

Momentum would also change since mass flux affects how fast the balls are moving.

Exactly right! Understanding this interplay is crucial for predicting fluid behavior in real-world applications.
Conclusion and Key Takeaways
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To wrap up, we learned about the importance of mass and momentum fluxes in fluid mechanics. What are some key differences we noted?

That laminar flows are smooth and orderly, while turbulent flows are chaotic and fluctuating.

Correct! The behavior of fluid balls helps us visualize these concepts. Remember the significance of the Reynolds number and how it discriminates between flow types.

And how fluctuating velocities contribute to energy losses?

Exactly! All these components help us design better fluid systems in engineering. Great questions today!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section covers the principles of mass and momentum flux in the context of laminar and turbulent flows, using virtual fluid balls as a conceptual tool to illustrate how these flows interact. It also emphasizes the transitions between flow types as characterized by the Reynolds number, detailing the significance of fluctuations in velocity components.
Detailed
Mass and Momentum Flux Components
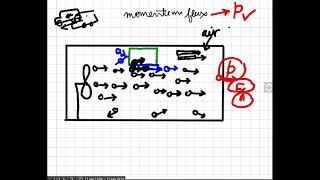
In fluid mechanics, the behavior of fluids in motion can be understood through the analysis of mass and momentum flux components. This section introduces the concept of virtual fluid balls to help visualize the dynamics of fluid motion during laminar and turbulent flows. As these 'balls' travel through different zones of turbulence, they may disintegrate or integrate depending on the turbulence intensity, affecting both mass and momentum transport.
The introduction of the virtual fluid ball analogy helps explain how turbulence increases the complexity of flow patterns, leading to energy loss and the formation of eddies. The turbulent nature of the flow results in irregular fluctuations and mixing, which contrasts with the orderly layer characteristics of laminar flow. The transition points between these flow regimes are defined by Reynolds numbers: flows below 2300 are laminar, between 2300 and 4000 represent transitional states, and flows above 4000 are classified as turbulent. Understanding these concepts is essential for designing efficient fluid transport systems in various engineering applications.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Turbulence and Virtual Fluid Balls
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now coming to the virtual fluid balls. As I said it that earlier we are looking to conceptualized fluid mechanics considering there are series of balls are moving from one place to other place. If I have a different fluids, I can have different colors of the balls, different sizes of the balls, and different masses of the balls.
Detailed Explanation
In fluid mechanics, we use the concept of virtual fluid balls to visualize how fluids flow. Imagine that each different fluid can be represented by balls of different colors and sizes. For instance, water might be represented by blue balls of a certain size, while oil might be represented by yellow balls of a larger size. These balls help us understand how the liquids move or interact under various conditions, such as turbulence.
Examples & Analogies
Think of a busy highway where cars (representing fluid balls) of various models and colors (representing different fluids) are moving. Just like different vehicles might speed up, slow down, or change lanes, fluid balls interact differently depending on their environment, such as whether they are in a calm area (laminar flow) or a crowded area (turbulent flow).
Disintegration of Fluid Balls in Turbulence
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When you have a turbulent flow, mostly you can imagine that these fluid balls are going to disintegrate or integrate depending upon the turbulence behavior... As they disintegrate, there are actions of mass fluxes as well as actions of the momentum flux.
Detailed Explanation
In turbulent flow, these virtual fluid balls do not remain intact. They break apart or disintegrate into smaller balls due to the chaotic nature of the turbulence. This disintegration leads to variations in mass and momentum flux, which are crucial for maintaining the movement of fluid. These changes in how fluid is transported vertically and horizontally are key characteristics of turbulent fluid behavior.
Examples & Analogies
Imagine a blender mixing a smoothie. Initially, you add whole fruits (the fluid balls), but once you turn on the blender (creating turbulence), those fruits disintegrate into smaller particles, helping to mix more evenly. Similarly, in turbulent flow, larger fluid clusters break into smaller entities, resulting in more efficient mixing and transport of substances.
Eddy Formation and Energy Dissipation
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you take a particular horizontal line, then you can visualize that there is a momentum flux and mass flux is going on that making a turbulence flow behaviors.
Detailed Explanation
As the fluid balls disintegrate, they can create whirlpool-like structures known as eddies. Eddies are circular movements within the fluid that carry mass and momentum across different layers. This process allows energy to be redistributed throughout the fluid. The presence of eddies is essential in understanding how energy dissipates in turbulent flows, leading to more complex flow behavior.
Examples & Analogies
Think of when you stir a cup of coffee. When the spoon moves through the liquid, it creates circular swirls, or eddies, that help distribute the sugar throughout. Similarly, in fluid flows, these eddies help transfer energy and materials within the moving fluid.
Concept of Mass and Momentum Flux
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now if you look it if I have an instrument to measure the velocity in the turbulent flow... So you will see these types of fluctuations.
Detailed Explanation
In turbulent flows, the velocity of the fluid is not uniform; it fluctuates from point to point. To analyze these flows, scientists measure the average velocity and the fluctuating components. The fluctuating velocity is essential because it affects how mass and momentum transfer occurs in the fluid. This understanding is crucial for applications like predicting how fluids behave in pipes and environmental systems.
Examples & Analogies
Imagine monitoring traffic on a highway. Some cars travel at a constant speed (average velocity), while others speed up or slow down (fluctuations). By understanding both the general speed trend and the individual variations, we can gain insights into traffic flow dynamics.
Components of Momentum Flux
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
As you know it... additional mass flux in the x directions.
Detailed Explanation
Momentum flux refers to the amount of momentum being transferred through a unit area in a particular direction. In fluid mechanics, the momentum flux can vary in different directions (x, y, z), especially when accounting for fluctuating components. Understanding how these components interact allows us to predict the forces at play in turbulent flows.
Examples & Analogies
Think of a factory conveyor belt carrying boxes. The speed at which boxes move is like momentum flux. If some boxes are pushed harder (fluctuation), they may transfer their momentum differently compared to boxes moving steadily, affecting how the entire system operates.
Key Concepts
-
Mass Flux: The rate of mass transfer through a unit area.
-
Momentum Flux: The rate of momentum transfer through a unit area.
-
Reynolds Number: A dimensionless value indicating flow type.
-
Turbulence: The chaotic flow regime characterized by fluctuations and mixing.
Examples & Applications
Example of laminar flow can be seen in a low-speed water stream where the water layers slide past each other smoothly.
In turbulent flow, like that seen in a fast-moving river, the water exhibits swirling eddies and chaotic patterns.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In laminar flow, smooth and slick, / Turbulent flow is a wild trick. / Balls break apart, mass flows tonight, / Energy lost in chaotic flight.
Stories
Imagine a river flowing gently. This is our laminar ball gliding smoothly. Suddenly, a storm brews, causing the balls to clash and scatter, representing turbulent flow where chaos reigns.
Memory Tools
Remember LTR: Laminar, Transitional, Turbulent flow — the flow types based on Reynolds number!
Acronyms
M&M for Mass and Momentum — the two crucial flux components in fluid dynamics!
Flash Cards
Glossary
- Laminar Flow
A smooth, orderly fluid motion characterized by parallel layers.
- Turbulent Flow
Fluid motion that is chaotic and characterized by eddies and irregular fluctuations.
- Reynolds Number
A dimensionless number used to predict flow patterns in different fluid flow situations.
- Mass Flux
The mass flow rate per unit area, indicating how much mass passes through a given cross-section.
- Momentum Flux
The momentum flow rate per unit area, signifying how momentum is transported through a fluid.
Reference links
Supplementary resources to enhance your learning experience.
