Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Energy Dissipation in Fluid Mechanics
Unlock Audio Lesson
Today, we're going to discuss energy dissipation in fluid mechanics, particularly focusing on different flow types. Can anyone tell me what laminar flow is?
Laminar flow is when fluid moves in parallel layers without mixing.
Exactly! In laminar flow, at low Reynolds numbers, energy dissipation is minimal because the layers slide past each other smoothly.
What happens to energy dissipation when the flow becomes turbulent?
Good question! As we move into turbulent flow, which occurs above a Reynolds number of 4000, energy dissipation increases significantly due to chaotic motion and mixing of the fluid.
Can you explain how this relates to fluid transport in pipes?
Of course! Understanding energy dissipation helps in designing more efficient pipe systems, ensuring minimal energy loss during transport.
Exploring Reynolds Number and Flow Types
Unlock Audio Lesson
Let’s dive deeper into the Reynolds number. Who can summarize what it represents?
The Reynolds number measures the ratio of inertial forces to viscous forces in fluid flow.
Exactly! When the Reynolds number is below 2300, we have laminar flow, like a smooth river. Above 4000, it becomes turbulent, resembling rapids with lots of mixing.
What about the region between the two?
Great question! That transition region is unstable, where the flow can fluctuate between laminar and turbulent states.
How does this affect energy efficiency in systems?
The main goal is to maintain flow as laminar in systems where energy loss must be minimized. However, turbulent flow is often necessary for efficient mixing.
Understanding Turbulence and Energy Dissipation
Unlock Audio Lesson
Now, let’s talk about turbulence. How would you describe its effects on energy dissipation?
It increases energy dissipation because of chaotic movements and mixing!
Exactly! Turbulent flow introduces irregular fluctuations that significantly increase energy loss.
I remember you mentioned virtual fluid balls. Could you explain how they relate to turbulence?
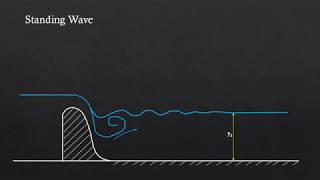
Absolutely! In a turbulent flow, these virtual balls will disintegrate and regroup, leading to the formation of eddies, which are crucial for momentum and mass transport.
How can we visualize turbulence effectively?
We often use experiments like the Reynolds apparatus that illustrate flow behavior through dye injection. This vividly shows the transition from laminar to turbulent flow.
Practical Applications of Energy Dissipation Concepts
Unlock Audio Lesson
Finally, let’s link our discussion back to real applications. Can anyone think of where efficient energy dissipation is crucial?
In designing water supply systems or pipelines!
Exactly! Engineers must account for energy losses to ensure that the systems function efficiently.
What about environmental applications?
Great point! Environmental systems, like rivers and stormwater drainage, require understanding of flow types to manage pollution dispersion effectively.
So, understanding these concepts really helps in various fields!
Absolutely! Energy dissipation is fundamental in fluid dynamics, exploring everything from industrial applications to environmental management.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the conceptual framework behind energy dissipation in laminar and turbulent flows. It introduces key concepts such as the Reynolds number and the distinction between laminar and turbulent flow regimes, emphasizing their practical relevance in fluid systems, particularly in industrial applications.
Detailed
Energy Dissipation
In fluid mechanics, energy dissipation is a critical concept, particularly when analyzing laminar and turbulent flows. Laminar flow occurs at low Reynolds numbers (below 2300), where the fluid moves in parallel layers, resulting in minimal energy loss due to internal friction. When the flow transitions into the turbulent regime (above 4000), the energy dissipation significantly increases due to chaotic fluctuations and mixing of fluid particles. This section explores the features of turbulent flows, including the disintegration and integration of virtual fluid balls, which serve as a useful model for understanding mass and momentum transport. Additionally, experiments such as the Reynolds apparatus illustrate these principles by visually demonstrating flow patterns and behaviors under varying conditions. Understanding these dynamics is crucial for designing efficient fluid transport systems, which have widespread applications in engineering and environmental science.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Turbulent Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now coming to the virtual fluid balls. As I said it that earlier we are looking to conceptually the fluid mechanics considering there are series of the balls are moving from one place to other place.
Detailed Explanation
In fluid mechanics, we often use the concept of virtual fluid balls to represent the movement of fluid. These can be imagined as small, colored balls (representing fluid particles) floating and moving through a medium. This visualization helps in understanding how fluids behave, particularly in turbulent conditions where the fluid movement becomes chaotic and complex.
Examples & Analogies
Think of a crowded swimming pool where people are splashing around. Each person represents a virtual fluid ball. If everyone is swimming calmly in a straight line, the pool is like laminar flow. However, if some people start splashing around wildly, this chaos represents turbulent flow. Just like the swimmers collide and change direction, in turbulent flow, fluid particles mix and change paths dramatically.
Disintegration and Integration of Fluid Balls
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When you have a turbulent flow, mostly you can imagine is that this fluid balls are going to disintegrated or integrated depending upon the turbulence behavior.
Detailed Explanation
In turbulent flow, the virtual fluid balls can break apart (disintegrate) or come together (integrate). This behavior is driven by the turbulence present in the flow. In high turbulence zones, larger fluid balls break into smaller ones, altering the way mass and momentum are distributed throughout the fluid. As these smaller balls move at different velocities, they contribute to the overall dynamics of the flow.
Examples & Analogies
Imagine throwing a bouncy ball into a turbulent stream. Initially, the ball represents a larger fluid particle. As it hits the rough water, it may shatter into smaller pieces (disintegrate), which then scatter in different directions. Each little piece behaves differently, affecting how the entire stream appears as it flows – similar to how smaller fluid particles behave in turbulence.
Eddy Formation in Turbulence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As the disintegrated smaller balls group together and create some sort of vortex formula, which will be called eddies.
Detailed Explanation
When fluid particles disintegrate, they can form clusters or vortices, known as eddies. Eddies are swirling motions in fluid that play a significant role in the transport of mass and momentum. These structures can vary greatly in size, and their dynamics are fundamental in understanding how energy is dissipated in turbulent flows.
Examples & Analogies
Picture a whirlpool in a river. The spinning motion of water around the whirlpool's center represents the eddies created by fluid particles. The water inside the whirlpool is constantly moving, exhibiting energy loss as it interacts with the surrounding currents, much like energy dissipation in turbulent flow.
Energy Dissipation Mechanism
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The smaller eddies again dissipated it due to the high viscosity zones. So there are the zone of turbulence generations.
Detailed Explanation
Energy dissipation in turbulent flows occurs when eddies become smaller and eventually lose their energy due to the viscosity of the fluid. High viscosity zones resist motion, causing the kinetic energy of the eddies to convert into thermal energy. This process leads to the overall loss of energy in the flow system, essential for understanding fluid mechanics and designing efficient systems.
Examples & Analogies
Consider a pot of boiling water. As the water heats up, bubbles form and create small whirlpools. These bubbles (like eddies) move quickly and then disappear as they lose energy to the surrounding cooler water. Similarly, in turbulent flow, the constant generation and destruction of eddies mean that energy is continuously being absorbed and dissipated.
Transition from Laminar to Turbulent Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The threshold of the Reynolds number that changes from laminar to transitions and transitions to the turbulent flow.
Detailed Explanation
The flow of fluids transitions from laminar to turbulent based on the Reynolds number, a dimensionless value that describes the ratio of inertial forces to viscous forces in the fluid. When the Reynolds number is below a certain threshold (typically 2300), the flow remains laminar. As it approaches 4000, the flow becomes turbulent. Understanding these thresholds is essential for predicting flow behavior in engineering applications.
Examples & Analogies
Imagine riding a bike in a calm park versus riding through a strong wind. In the calm park, you move smoothly (laminar flow). As the wind picks up speed, it pushes against you, causing you to wobble and struggle (turbulent flow). Just like the transition from smooth to chaotic riding reflects the transition from laminar to turbulent flow.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Energy Dissipation: The process of losing kinetic energy in fluid due to friction and turbulence.
-
Laminar Flow: A smooth, orderly fluid motion characterized by parallel layers.
-
Turbulent Flow: A chaotic flow regime with significant mixing and irregular fluctuations.
-
Reynolds Number: A dimensionless value indicating the flow regime based on inertial and viscous forces.
-
Eddies: Swirling movements in turbulent flow that enhance mixing and momentum exchange.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The flow of honey in a pipe is a good example of laminar flow, where layers slide smoothly.
-
The turbulent flow in a river seen at high speeds, where water mixes creating chaotic currents.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In laminar flow, it's smooth and slow, / Turbulent flow puts on a show.
📖 Fascinating Stories
-
Imagine a calm river flowing gently. As the speed increases, whirlpools form, representing turbulent flow, highlighting how energy dissipates in chaos.
🧠 Other Memory Gems
-
Remember L-T-RE for Flow Types: Laminar (L), Turbulent (T), Reynolds number (R), Energy dissipation (E).
🎯 Super Acronyms
FLOWS - Friction, Laminar, Oscillation, Whirls, and Shear signify the fluid behaviors!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Energy Dissipation
Definition:
The loss of mechanical energy in a fluid due to viscous friction and turbulence.
-
Term: Laminar Flow
Definition:
A flow regime characterized by smooth, orderly fluid motion in parallel layers.
-
Term: Turbulent Flow
Definition:
A flow regime marked by chaotic fluid motion and significant mixing.
-
Term: Reynolds Number
Definition:
A dimensionless number that predicts flow regimes, calculated as the ratio of inertial forces to viscous forces.
-
Term: Eddy
Definition:
A localized swirling motion in a fluid, usually found in turbulent flows.