Irrotational Flow
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Irrotational Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we're going to explore irrotational flow. Can anyone tell me what they think it means?

I think it means that the fluid particles don’t spin or rotate, right?

Exactly! Irrotational flow indicates that outside specific zones, such as boundary layers, fluid particles move without rotation. This is essential for predicting fluid behavior.
Boundary Layer Formation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's discuss boundary layers. Who can explain what they are?

Are they the thin regions near a surface where the flow is affected by viscosity?

Correct! In boundary layers, you'll see significant velocity gradients, causing fluid particles to start rotating, in contrast with the irrotational flow outside of them.

So, the fluid really behaves differently inside and outside these layers?

Yes! Inside the boundary layers is where we see vorticity due to these rotational movements.
Understanding Vorticity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's talk about vorticity. How do you think this is defined?

Is it the measure of rotation in a fluid?

Yes! It's defined as the curl of the velocity field. In irrotational flows, the vorticity is zero, while in rotational flows, it’s non-zero.

So, if vorticity can tell us about rotation, does that mean we can use it to predict flow patterns?

Absolutely! Vorticity plays a crucial role in understanding complex fluid dynamics like cyclones.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section discusses irrotational flow and its characteristics, particularly focusing on boundary layer formation where viscous effects lead to rotational movement of fluid particles. It contrasts the rotational flow found within boundary layers with the irrotational flow beyond, providing insights into concepts such as vorticity, velocity gradients, and the significance in real-world applications like fluid dynamics and cyclones.
Detailed
Irrotational flow is a key concept in fluid mechanics, signifying the flow of fluid where particles do not rotate, particularly outside the boundary layers. In boundary layers, significant velocity gradients cause fluid particles to experience rotational motion, leading to the generation of vorticity, which is defined mathematically as the curl of the velocity field. The section illustrates how visualization aids understanding, using examples from flow around objects to characterize regions of rotational versus irrotational flow. It emphasizes the significance of these concepts in applications like predicting cyclones and understanding viscosity effects in fluid dynamics.
Youtube Videos

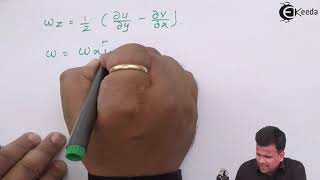






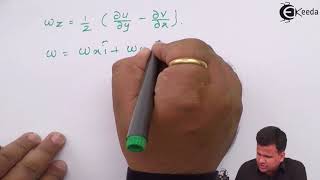
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Flow and Boundary Layers
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
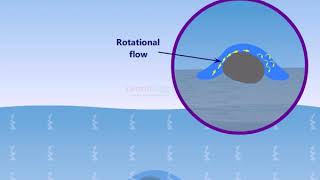
I think you please remember these figures okay which is very interesting figures for a fluid mechanic student point of view that when you have this a flow passing over the plate, you can anticipate it that you will have a viscous effect zone which is called boundary layer formations, there is a zone where there is large gradient of velocity vectors, the velocity will start from 0 to a large gradient will be there.
Detailed Explanation
When fluid flows over a surface, it doesn't move uniformly; instead, it forms a region known as the boundary layer. In this zone, there's a significant change in the speed of the fluid, starting from zero at the surface (where it's at rest) to higher speeds further away from the surface. Understanding this is crucial as it leads to the development of various flow characteristics.
Examples & Analogies
Imagine a river flowing over rocks. Near the rocks, the water moves slowly because of friction. Further out, the water moves faster. The slow-moving water closest to the rocks represents the boundary layer.
Velocity Gradient and Turbulence
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Since, there is a large gradient of velocity variation is there as I said it earlier that velocity vector change from one point to other point, so the fluid particles will not go straight line, they will start rotating it, so that way this figure is retreating that when the fluid particles entered here, there are large velocity gradients are there, the turbulence is there, so the boundary layer formations are the zone where viscous effect dominates okay.
Detailed Explanation
The boundary layer has a high gradient of velocity, which means the speed of the fluid changes dramatically over a short distance. This leads to rotational motion in the fluid particles due to the shear stress acting within the fluid, increasing the complexity of the flow. Essentially, the interconnected motions within this layer create turbulence, further complicating the flow dynamics.
Examples & Analogies
Think of the wind blowing through tall buildings in a city. Near the buildings, the wind is affected by their shape and speed changes rapidly, causing turbulence as compared to the open space higher up.
Understanding Irrotational Flow
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, then we tell it irrotational fluid, this is the outside of the boundary layers, you can see that fluid particles are moving it or the virtual fluid balls are moving it without any rotations but within the boundary layer formations, the small regions near to a surface, you will see there is a change of the velocity gradients; the drastic change of the velocity gradient and those the regions; a thin region is called boundary layer.
Detailed Explanation
Outside of the boundary layer, the fluid can be considered irrotational. This means the fluid particles move in a straight path without spinning or changing direction. On the other hand, within the boundary layer, due to the high gradients in velocity and the viscous effects, the fluid experiences rotational movements. This contrast is key in fluid mechanics to differentiate between pure flow and flow with significant interference from surfaces.
Examples & Analogies
Picture riding your bike in an open field where the wind flows smoothly around you (irrotational) versus riding next to a wall where the air swirls and creates a chaotic pattern (rotational).
Effects of Vorticity in Fluid Flow
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
There; because there is large variations of velocity factors induces the fluid particles to start rotating it, once you start rotating it so, once particles start rotating, other one will start rotating it and that what it is having formations of Eddies formations and all which we will discuss in the later on in a pipe flow chapters.
Detailed Explanation
The variations in velocity within the boundary layer lead to particles of fluid beginning to rotate, creating a phenomenon known as vorticity. When one particle starts rotating, it influences its neighboring particles, resulting in organized patterns of swirling motion, known as eddies. This is important in understanding how fluids interact with surfaces and themselves.
Examples & Analogies
Consider swirling a spoon in a bowl of water; the moving spoon creates circular eddies in the water as particles nearby pick up on the motion and start to swirl as well.
Vorticity and Angular Rotation
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, that what we measure in terms of vorticity, so please do not have a very confusion between the vorticity and angular vector because vorticity is easy to define is a cross product between the delta and the V where is when you talk about angular rotations, we have half of that so, it is very easy the people who are not looking at the angular rotations, they are looking at it in terms of how the vorticity is playing it or vortex formations happening it.
Detailed Explanation
Vorticity is a mathematical construct used to describe the local spinning motion of fluid and is calculated from the velocity gradient. It’s different from angular velocity, which refers to overall rotational motion. Understanding vorticity is crucial for analyzing the flow behavior around objects and predicting turbulence in fluid systems.
Examples & Analogies
Think of how a tornado rotates: while the entire tornado has a motion (angular rotation), the individual air particles spiral around the center at different rates. Vorticity helps us understand those individual spins.
Irrotational Flow Examples
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
These are very examples as I said it that when the fluid particles outside the boundary layer has a zero vorticity non-rotational zone but inside the boundary layers, it will have non zero vorticity, so flow is a rotational, air is still surrounding the irrotational but it is obstructed by object or these things, so air flow wherever is that if there is no obstructions, so it will be the irrotational.
Detailed Explanation
In fluid dynamics, the distinction between irrotational and rotational flows is highlighted by the presence of vorticity. Outside the boundary layer, fluids flow without rotational influence (zero vorticity), while within the boundary layer, interactions with surfaces introduce rotational characteristics (non-zero vorticity). Understanding this helps engineers design better systems where efficiency is crucial, like aircraft wings, where azimuthal flow can significantly affect lift.
Examples & Analogies
Picture a flat road while driving: if there are no obstructions, the air flows smoothly past your car (irrotational). But, what if you drove through a windy street? The air may swirl around buildings and trees, creating eddies (rotational).
Key Concepts
-
Irrotational flow: Describes non-rotating fluid motion, primarily observed outside boundary layers.
-
Boundary layers: Thin regions where viscous effects dominate, leading to rotational flow of fluid particles.
-
Vorticity: Defined as the curl of the velocity field, representing the degree of local rotation within the fluid.
Examples & Applications
Aerodynamic flow over an airplane wing creates a boundary layer where viscosity affects the flow characteristics.
In predictably circular flows, like those in cyclones, understanding vorticity helps forecast severe weather patterns.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Irrotational is plain and clean, moving straight, no whirl or lean.
Stories
Imagine two rivers: one flows smoothly without bends, while the other spins wildly, creating whirlpools. The first river is irrotational.
Memory Tools
IRR - Irrotational Flow Reigns: No rotation in irrotational flow.
Acronyms
B.L.A. - Boundary Layer Formation leads to Altered flow.
Flash Cards
Glossary
- Irrotational Flow
A type of fluid motion where fluid particles do not undergo rotation.
- Boundary Layer
A thin layer of fluid in the vicinity of a boundary, where viscous effects are significant.
- Vorticity
A measure of the local rotation in a fluid, defined mathematically as the curl of the velocity field.
Reference links
Supplementary resources to enhance your learning experience.
