Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Boundary Layer Concepts
Unlock Audio Lesson
Today, we are diving into boundary layers. Can anyone explain what happens when a fluid flows over a surface?
The fluid experiences different velocities as it nears the surface.
Yes! Specifically, the fluid starts from rest at the surface and gains velocity away from it. This region is crucial because it's called the **boundary layer**.
Why is this boundary layer important?
Great question! The boundary layer influences drag in bodies, affects heat transfer, and promotes flow separation.
What about the velocity gradient inside the boundary layer?
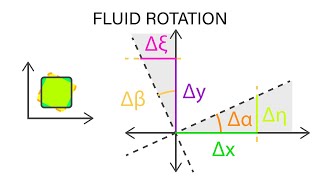
Exactly! There's a large gradient of velocity inside, which causes the particles to start rotating.
To remember this, think of the acronym **B.R.A.V.O.**: Boundary layer - Rotational flow - Acceleration - Vorticity - Obstruction.
I’ll definitely remember that!
To summarize, we just learned about the significance of boundary layers and how velocity gradients induce rotations. Remember, the boundary layer plays a vital role in fluid dynamics.
Understanding Vorticity
Unlock Audio Lesson
Now let’s shift focus to vorticity. Who can explain what vorticity measures in a flow?
Isn't it the measure of the rotation of fluid particles?
"Correct! Vorticity essentially captures how much and how fast a particle is rotating. Mathematically, we define it as the cross product of the gradient operator and the velocity vector, or
Distinguishing between Rotational and Irrotational Flows
Unlock Audio Lesson
Next, let's talk about rotational versus irrotational flows. Can anyone define the difference?
Rotational flow has vorticity, while irrotational flow doesn’t.
Right! In a rotational flow, vorticity is non-zero. Close to a surface, we observe this 'twisting', whereas the flow far from obstacles is termed irrotational because fluids move parallel without any rotations.
What happens in practical scenarios?
Excellent question! In engineering, we use this understanding to design efficient wings and turbines, recognizing where the flow becomes turbulent or remains clean and efficient.
Can you give an example of irrotational flow?
Certainly! A common example is the smooth flow around a perfect sphere in an ideal fluid, where the flow remains irrotational far from the object.
For memory, think **I.R. for Irrotational**: Ideal flow with no rotation!
That helps a lot!
To wrap up, we’ve distinguished between rotational and irrotational flows, with real-world applications in engineering designs and their importance for fluid dynamics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on how fluids behave when they flow over surfaces, particularly the concept of boundary layers where velocity gradients and rotational behavior are prominent. Key terms like vorticity, irrotational flow, and their mathematical representations are introduced, along with examples to illustrate the phenomena.
Detailed
Detailed Summary of Rotation
This section explores critical concepts in fluid mechanics related to rotation, particularly focusing on the behavior of fluid particles as they flow over surfaces. When fluid flows over a plate, it generates a boundary layer where velocity gradients are substantial, causing fluid particles to exhibit rotational behavior.
Key terms introduced in this section include vorticity, which measures the rotation of fluid particles in a flow field, and the distinction between irrotational and rotational flows. Outside the boundary layer, the flow is considered irrotational, as fluid particles move without rotation. Inside the layer, however, the velocity gradients drive the particles to rotate, forming vortices and eddies.
Mathematically, vorticity is defined as the cross product of the del operator and the velocity vector (
∇ × V), and it becomes a fundamental aspect to analyze flow behavior in engineering applications, particularly in turbine machinery and environmental fluid mechanics. Examples and figures provided in the section aid in visualizing these concepts and help reinforce the understanding of how rotation and vorticity apply to real-world scenarios, such as cyclone patterns.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Boundary Layer Formation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
I think you please remember these figures okay which is very interesting figures for a fluid mechanic student point of view that when you have this a flow passing over the plate, you can anticipate it that you will have a viscous effect zone which is called boundary layer formations, there is a zone where there is large gradient of velocity vectors, the velocity will start from 0 to a large gradient will be there.
Detailed Explanation
When a fluid flows over a surface, like a flat plate, it doesn't move at a uniform speed. Near the plate, the velocity is zero because the fluid particles are stuck to the solid surface due to viscosity. As you move away from the surface into the fluid, the velocity increases until it reaches a maximum. This region where the velocity changes from zero to its maximum is known as the boundary layer. In this zone, viscous effects are significant and impact how the fluid flows. The changes in velocity create varying speeds and lead to rotational motion in fluid particles, especially within this boundary layer.
Examples & Analogies
Imagine when you run your hand through water. Your hand moves quickly, but near your hand (close to your skin), the water is still and moves more slowly. This is similar to how the fluid behaves close to a surface, creating a layer of slower-moving fluid alongside faster-moving fluid further away.
Vortex Formation and Rotation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Since, there is a large gradient of velocity variation is there as I said it earlier that velocity vector change from one point to other point, so the fluid particles will not go straight line, they will start rotating it, so that way this figure is retreating that when the fluid particles entered here, there are large velocity gradients are there, the turbulence is there, so the boundary layer formations are the zone where viscous effect dominates okay.
Detailed Explanation
As fluid flows, variations in speed lead to changes in the direction of movement of fluid particles. Instead of flowing in parallel lines, particles experience rotational motion due to the differences in velocity across the boundary layer. This rotation contributes to the formation of vortices or eddies, where fluid particles spin around an axis. The presence of these eddies can significantly change the flow characteristics, indicating the complexity of fluid movement in real-world scenarios.
Examples & Analogies
Picture a swirling drain in a sink: water moves in straight lines toward the drain, but as it approaches, it starts to spiral. This spiral motion is akin to the rotational effect experienced by fluid particles within the boundary layer.
Irrotational Fluid Behavior
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, then we tell it irrotational fluid, this is the outside of the boundary layers, you can see that fluid particles are moving it or the virtual fluid balls are moving it without any rotations but within the boundary layer formations, the small regions near to a surface, you will see there is a change of the velocity gradients; the drastic change of the velocity gradient and those the regions; a thin region is called boundary layer.
Detailed Explanation
In regions outside the boundary layer, the fluid flows smoothly without rotation; this is referred to as an irrotational flow. The fluid particles exhibit translational movement, meaning they slide past each other in a uniform manner without spiraling. However, within the boundary layer, there is considerable change in velocity gradients, causing the rotational behavior in particle motion due to the viscosity of the fluid.
Examples & Analogies
Think of a soccer ball rolling perfectly on a smooth field. The ball moves straight without any spinning. However, as it hits the grass at the edge of the field, the ball may wobble or rotate due to the uneven surface. This is similar to how fluids behave: smooth motion in irrotational regions and more chaotic behavior in boundary layers.
Understanding Vorticity and Its Measurement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So that what we measure in terms of vorticity, so please do not have a very confusions between the vorticity and angular vector because vorticity is easy to define is a cross product between the delta and the V where is when you talk about angular rotations, we have half of that so, it is very easy the people who are not looking the angular rotations, they are looking it in terms of how the vorticity is playing it or vortex formations happening it, they talk about at the vorticity level not at the rotations level.
Detailed Explanation
Vorticity is a measure of the local rotation within a fluid. It's calculated as the cross product of the velocity gradient and the velocity vector. Unlike simple angular momentum, vorticity provides insight into the rotational behaviors of fluid elements. Understanding vorticity is crucial for comprehending swirling flows and turbulent patterns of movement in fluids.
Examples & Analogies
Consider the spinning motion of a whirlpool in water. The vorticity gives you a measure of how intense and how fast the water is rotating at any point in the whirlpool. Just as a whirlpool shows turbulence, vorticity helps predict the behavior of fluids in diverse conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Boundary Layers: Essential for understanding flow behavior near surfaces.
-
Vorticity: Crucial for assessing rotational motion in fluid dynamics.
-
Rotational Flow: Important for understanding turbulence and energy loss in flows.
-
Irrotational Flow: Significant in ideal fluid flow scenarios and theoretical studies.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The boundary layer developing on a flat plate leads to drag forces in aircraft designs.
-
Cyclones exhibit areas of high vorticity, demonstrating the principles of rotational flow in nature.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In flows that twist and turn, / Vorticity's what we learn.
📖 Fascinating Stories
-
Imagine a dance where the dancers twirl around each other. This dance illustrates rotational flow, where each dancer represents a fluid particle.
🧠 Other Memory Gems
-
Remember B.I.V. for Boundary - Irrotational - Vorticity.
🎯 Super Acronyms
Use the acronym **R.I.P.** to remember Rotational - Irrotational - Particle behavior.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Boundary Layer
Definition:
The thin layer of fluid near a surface where velocity changes from zero at the surface to the free-stream velocity.
-
Term: Vorticity
Definition:
A measure of the local rotation of a fluid element, quantified as the curl of the velocity field.
-
Term: Rotational Flow
Definition:
Flow in which fluid particles exhibit rotational motion, characterized by non-zero vorticity.
-
Term: Irrotational Flow
Definition:
Flow in which fluid particles move without rotation, characterized by zero vorticity.