Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Boundary Layers
Unlock Audio Lesson
Let's start by discussing boundary layers in fluid flow. When a fluid flows over a plate, do you notice any effects?
I've heard that there's something called a boundary layer that forms?
Exactly! The flow near the surface has a velocity starting from zero and gradually increasing, creating a velocity gradient. This region is what we call the boundary layer.
What happens to the fluid particles within that boundary layer?
Great question! The large velocity gradients lead to fluid particles starting to rotate. This spinning of particles gives rise to vorticity.
Is that the same as the rotational motion we learned about before?
Not quite! Vorticity is a specific measure of the rotation of a fluid at a point, while rotational motion can refer to overall spinning. Think of it like an orange peel — where the peel represents rotational motion, and the juices inside represent vorticity.
Got it! So, the boundary layer affects how the fluid moves across the surface?
Exactly! Now, let's summarize: a boundary layer forms due to velocity gradients, leading to rotation of particles, represented by vorticity, while outside this layer, the flow is irrotational.
Vorticity and Rotational vs. Irrotational Flow
Unlock Audio Lesson
Now that we understand boundary layers, let’s dive into vorticity. What do we mean by rotational and irrotational flows?
Are rotational flows like the ones where the fluid spins around?
Yes, spots that have non-zero vorticity demonstrate rotation. For instance, the wake behind a spinning fan shows rotational flow.
And what about irrotational flow?
Irrotational flow has zero vorticity. Think of a Ferris wheel — while the chairs rotate in a circular path, the air surrounding it can be considered irrotational.
So, outside the boundary layer, the flow is still, but inside it’s all spinning?
Precisely! The key takeaway is that vorticity captures the essence of fluid rotations, distinguishing between these two types of flows.
I see how important vorticity is now in analyzing how fluids behave.
Yes! Let’s summarize: rotational flow has vorticity due to spinning while irrotational flow maintains a straight motion without rotation.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains the formation of boundary layers during fluid flow over surfaces, highlighting how velocity gradients lead to variations in rotational motion within the fluid. It distinguishes between rotational and irrotational flows and introduces important concepts like vorticity and angular rotation.
Detailed
Detailed Summary
In this section, we explore the phenomenon of linear strain and boundary layer formations in fluid mechanics. When fluid flows over a surface, it experiences viscous effects that give rise to what we term boundary layers. Within these layers, there are significant velocity gradients ranging from zero at the surface to higher speeds away from the surface.
The presence of large velocity gradients is crucial as it causes the fluid particles to begin to rotate, creating areas of vorticity. Vorticity is defined mathematically as a cross product of the del operator and the velocity vector, reflecting the rotational characteristics of fluid particles. Conversely, fluid outside the boundary layer remains irrotational, moving in a straight line without rotation. This fundamental distinction has important implications for understanding fluid motion and phenomena such as turbulence and eddy formations.
The section also contrasts rotational and irrotational flows, providing real-world examples like a Ferris wheel (irrotational) and a spinning top (rotational). By understanding these concepts, students can better grasp complex fluid dynamics and applications relevant to engineering, such as in turbomachinery operations and predictions of cyclone behavior.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Boundary Layer Formation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
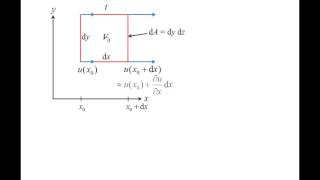
When you have a flow passing over a plate, you can anticipate that you will have a viscous effect zone, called boundary layer formations. There is a zone where there is a large gradient of velocity vectors, and the velocity will start from 0 to a large gradient.
Detailed Explanation
This chunk introduces the concept of boundary layers in fluid mechanics. When a fluid flows over a surface, the layers of fluid closest to the surface experience viscous (friction) forces that slow them down, forming what is known as a boundary layer. In this layer, the velocity of the fluid changes rapidly from zero at the surface (due to no-slip conditions) to a higher speed as you move away from the surface.
Examples & Analogies
Think of a wall covered in paint. If you blow air across the surface of the wall, the air in contact with the wall moves much slower than the air further away because of friction. The air closest to the wall forms a boundary layer where its velocity gradually increases from zero (at the wall) to the speed of the air further away.
Effects of Viscosity and Turbulence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
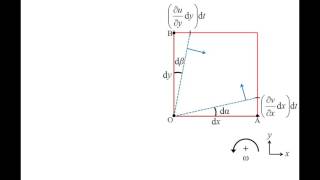
Due to the large gradient of velocity variation, fluid particles do not move in a straight line. They start to rotate, which is a characteristic of turbulent flow within the boundary layer.
Detailed Explanation
In regions with a high velocity gradient, such as within the boundary layer, the viscosity of the fluid causes the fluid particles to rotate rather than move straight. This rotational motion leads to the development of vortices and turbulence, which are important qualitative changes in the flow behavior that can affect the efficiency of fluid movement and the forces acting on surfaces.
Examples & Analogies
Imagine swirling a spoon in a cup of coffee. The coffee near the spoon rotates because of the spoon's motion (analogous to the boundary layer), while the coffee further away is relatively undisturbed. This swirling is similar to the rotational motion observed in turbulent flows where the velocity gradients are high.
Distinction Between Rotational and Irrotational Flows
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fluid particles outside the boundary layer have zero vorticity (non-rotational zone), but inside the boundary layers, there is non-zero vorticity, indicating rotational flow.
Detailed Explanation
This chunk explains the key distinction between two types of fluid flow: rotational and irrotational. In the irrotational flow, fluid particles do not exhibit any rotational motion, whereas in the rotational flow (typically within boundary layers), the particles do show rotational movement due to the velocity gradients. Understanding this distinction is crucial in fluid dynamics as it impacts how fluid flows and interacts with surfaces.
Examples & Analogies
Consider a merry-go-round. The people sitting on it (the fluid particles) rotate together, demonstrating rotational flow. In contrast, people standing outside the merry-go-round, not affected by its motion, represent irrotational flow; they simply move in a straight path and do not experience any rotation.
Measuring Vorticity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Vorticity can be defined by the cross product of the gradient operator and the velocity vector. It is distinct from angular rotation and helps in understanding the fluid's rotational characteristics.
Detailed Explanation
In fluid mechanics, vorticity is a measure of the local rotation at a point in the fluid. It is calculated using a mathematical operation involving the velocity field. Understanding vorticity is crucial for analyzing fluid flows, especially in situations where rotation affects the flow dynamics, such as predicting turbulence or managing flow around structures.
Examples & Analogies
Imagine a small whirlpool in a stream. The swirling motion of the water represents vorticity. Just like the whirlpool rotates around a center, vorticity shows how fluid rotates around a point. This concept is useful for engineers and scientists to predict how water (or air) flows in various environments.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Boundary Layer: The region in fluid flow where viscosity plays a significant role, causing velocity gradients.
-
Vorticity: The measure of the rotational motion of fluid particles, crucial for understanding fluid dynamics.
-
Rotational Flow: Represents areas of fluid with significant rotation and non-zero vorticity.
-
Irrotational Flow: Areas of fluid devoid of rotation, with vorticity equal to zero.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A fan's blade rotates air creating a rotational flow behind it, with notable vorticity visible.
-
The movement of a Ferris wheel is characterized as irrotational flow, with the air around it acting uniformly.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the flow where the boundary's near, viscous effects are crystal clear.
📖 Fascinating Stories
-
Imagine a river flowing over rocks. The water slows down at the surface but speeds back up - creating a boundary layer. Below the rocks, the water swirls, creating vorticity.
🧠 Other Memory Gems
-
BIR: Boundary layer, Irrotational flow, Rotational flow.
🎯 Super Acronyms
VIV
- Velocity gradients induce vorticity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Boundary Layer
Definition:
A region near a surface within which the effects of viscosity are significant and velocity gradients are present.
-
Term: Vorticity
Definition:
A measure of the local rotation of fluid particles, calculated as the curl of the velocity vector field.
-
Term: Rotational Flow
Definition:
A flow where fluid particles exhibit rotational motion and non-zero vorticity.
-
Term: Irrotational Flow
Definition:
A flow where fluid particles have zero vorticity and do not exhibit any rotational motion.