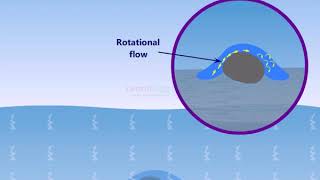
Rotational Flow
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Rotational Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome, everyone! Today we're diving into the world of fluid mechanics, specifically rotational flow. Can anyone tell me what they think rotational flow means?

I think it's when fluid particles spin around a point like in a whirlpool.

Exactly! Rotational flow refers to fluid motion where particles rotate around an axis. Now, what might cause this rotation?

It might happen near surfaces or obstacles, like a cylinder in water.

Correct! This leads us to the concept of boundary layers, where we see significant velocity gradients. Can anyone explain what happens in the boundary layer?

I think it’s where the velocity changes rapidly from zero at the surface to higher values above.

Perfect! This area experiences viscous effects and induces rotation in the particles. Great job!
Understanding Vorticity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s discuss vorticity. Can anyone describe what vorticity means in the context of fluid flow?

Isn't it a measure of how much a fluid element is rotating?

Exactly! Vorticity quantifies rotational motion. Now, what is the formula for vorticity?

It’s the cross product of the del operator and the velocity vector, right?

Well done! In regions with non-zero vorticity, we get rotational flows. What about outside the boundary layer?

That’s where the flow is irrotational.

Correct! Irrotational zones have uniform velocity and zero vorticity. Great discussion, everyone!
Boundary Layer Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s consider boundary layers in real life. How do they impact structures like airplanes and turbines?

They can create drag and affect lift, right? If the boundary layer is too thick, it can cause turbulence.

Exactly! Engineers must manage these effects to improve efficiency. What about cyclones or tornadoes?

They can have massive vortices due to rotational flow, affecting weather patterns.

Great example! Understanding these concepts is vital for fluid dynamics. Let’s keep this in context with our future discussions!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section explores key concepts in fluid mechanics, specifically rotational and irrotational flows, examining boundary layer formations and the significance of vorticity. It discusses the behavior of fluid particles in rotational flows and the implications for understanding fluid motion.
Detailed
Detailed Summary of Rotational Flow
In fluid mechanics, understanding the behavior of flows is crucial. This section delves into rotational flow, highlighting the concept of boundary layers where viscous effects dominate. When fluid flows over a surface, it generates a boundary layer characterized by a steep velocity gradient, leading to rotational flow as fluid particles start to rotate due to turbulence and velocity variations.
The section distinguishes between rotational and irrotational flows, examining the significance of vorticity, which is defined as the measure of rotational motion in fluid particles. Vorticity is derived from the cross product of the del operator and velocity vector. In regions outside the boundary layer, the flow is considered irrotational, indicating uniform velocity without rotations.
Moreover, the section touches on practical examples of flows affected by objects and the resultant boundary layer formations, including implications in engineering fields like turbomachinery. Through visual aids and figures, students are encouraged to conceptualize and differentiate between regions of rotational and irrotational flow, laying the foundation for more advanced fluid dynamics topics.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Boundary Layer and Viscous Effects
Chapter 1 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
I think you please remember these figures okay which is very interesting figures for a fluid mechanic student point of view that when you have this a flow passing over the plate, you can anticipate it that you will have a viscous effect zone which is called boundary layer formations, there is a zone where there is large gradient of velocity vectors, the velocity will start from 0 to a large gradient will be there.
Detailed Explanation
When fluid flows over a surface, like a plate, it doesn't flow uniformly. Instead, there is a region close to the surface called the 'boundary layer'. In this region, fluid particles experience viscous effects that slow them down due to friction. The velocity of the fluid changes rapidly from 0 (at the surface of the plate) to higher values as you move away from the surface, creating a large gradient of velocity.
Examples & Analogies
Imagine walking through a crowd. When you get close to a wall (representing the plate), you can’t move freely because you are squeezed next to it, while those farther away (like the fluid particles in the boundary layer) can move faster without obstruction.
Boundary Layer Formations and Turbulence
Chapter 2 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Since there is a large gradient of velocity variation is there as I said it earlier that velocity vector change from one point to other point, so the fluid particles will not go straight line, they will start rotating it, so that way this figure is retreating that when the fluid particles entered here, there are large velocity gradients are there, the turbulence is there, so the boundary layer formations are the zone where viscous effect dominates okay.
Detailed Explanation
As fluid moves and encounters variations in velocity, the particles can no longer move in straight lines; they begin to rotate. This rotation leads to turbulence within the boundary layer, where the chaotic fluctuations of velocity and direction are influenced by the viscosity of the fluid. The boundary layer is crucial because it determines how the fluid interacts with the surface.
Examples & Analogies
Think of how a spoon stirs honey in a cup. At first, the honey flows smoothly, but as it gets stirred (like the fluid becoming turbulent), you see swirls and rotations forming. This chaotic movement represents the turbulence in the boundary layer.
Vorticity: Definition and Measurement
Chapter 3 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Those regions you will see the vorticity would be there or you just have the cross product of the del and the V, will show the vorticity and the graphically, you can see the face of this one's okay, it is just a vorticity okay, it is a rotation, the fluid particles will go under the rotations.
Detailed Explanation
Vorticity is a measure of the rotational motion of fluid particles in the flow. Mathematically, it is defined as the curl (a type of derivation) of the velocity field (V). High vorticity values indicate strong rotations within the fluid, while low values suggest that the fluid is flowing smoothly and uniformly.
Examples & Analogies
Consider a tornado: the air rotates violently around the center. In fluid mechanics, we can measure how ‘twisty’ the air is using vorticity, similar to measuring the strength of the whirl in a tornado.
Irrotational and Rotational Flow Comparison
Chapter 4 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, then we tell it irrotational fluid, this is the outside of the boundary layers, you can see that fluid particles are moving it or the virtual fluid balls are moving it without any rotations but within the boundary layer formations, the small regions near to a surface, you will see there is a change of the velocity gradients; the drastic change of the velocity gradient and those the regions; a thin region is called boundary layer.
Detailed Explanation
Outside of the boundary layer, the fluid can be considered irrotational, meaning that the fluid particles move without any rotation. However, when you enter the boundary layer, the fluid starts to exhibit rotational characteristics due to the drastic changes in velocity. This distinction between irrotational and rotational flow is essential for understanding fluid behavior in engineering contexts.
Examples & Analogies
Picture a calm lake: the surface flows smoothly (irrotational). Now, imagine the water near a boat’s hull where the water churns and rotates (the boundary layer). The turbulent water represents rotational flow, while the calm lake represents the irrotational flow.
Vorticity and Angular Momentum Distinction
Chapter 5 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, that what we measure in terms of vorticity, so please do not have a very confusions between the vorticity and angular vector because vorticity is easy to define is a cross product between the delta and the V where is when you talk about angular rotations, we have half of that so, it is very easy the people who are not looking the angular rotations, they are looking it in terms of how the vorticity is playing it or vortex formations happening it.
Detailed Explanation
Vorticity and angular rotation are related but distinct concepts in fluid mechanics. Vorticity is a local property that describes the rotation of small fluid elements, while angular momentum represents the total rotational motion of an entire particle system. Understanding this distinction is crucial for analyzing fluid dynamics accurately.
Examples & Analogies
Imagine spinning a basketball in the air versus rotating it in your hands. The spin of the ball (vorticity) can change quickly depending on how you throw it. However, the overall spin of a whole team playing with balls (angular momentum) is a broader concept. Both are related but focus on different aspects of motion.
Vorticity in Different Coordinate Systems
Chapter 6 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Vorticity vector in Cartesian coordinates: (omitting equations due to complexity). Two dimensional flow in Cartesian coordinates: z component of velocity (w) = 0, u and v are independent of z.
Detailed Explanation
In fluid mechanics, we often express vorticity using different coordinate systems to simplify calculations. For example, in two-dimensional flows, the z-component of velocity can be neglected, leading to a simpler form of the vorticity expression, focusing only on the x and y components.
Examples & Analogies
Think of how a pizza chef throws dough into the air in a flat circle (2D). In this scenario, we only consider the circular movement of the dough on the plane, ignoring any vertical motion, just like ignoring the z-component in our vorticity calculations.
Real-World Applications of Vorticity
Chapter 7 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, if you look at these figures, you can understand it which is irrotational, which is a rotational okay and the figures which is there in here you can look it which is a rotational, which is a irrotational okay, because of that you enjoy this the wheel okay because of its irrotational circular flow.
Detailed Explanation
In real-world applications, differentiating between rotational and irrotational flows can help us design better aerodynamic shapes and understand phenomena like weather patterns, turbine designs, and more. The example of a Ferris wheel illustrates irrotational flow when moving smoothly versus the chaotic motion inside a tornado.
Examples & Analogies
Consider how a well-designed airplane wing takes advantage of irrotational flow to minimize drag, helping the plane to fly efficiently. Understanding these principles helps engineers create more effective designs.
Key Concepts
-
Rotational Flow: Fluid motion where particles rotate around an axis due to velocity gradients.
-
Irrotational Flow: Flow characterized by uniform velocity without rotation of fluid particles.
-
Vorticity: Quantifies the degree of rotation in fluid motion, calculated via the curl of velocity.
-
Boundary Layer: Region near a surface where flow velocity changes rapidly, influencing flow behavior.
Examples & Applications
In aerodynamics, the boundary layer over an airplane wing affects lift and drag.
In weather systems, cyclonic vortices demonstrate rotational flow with significant impacts.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a whirlpool, water flows around, rotational joy is what we've found!
Stories
Imagine a tornado swirling through the sky, it spins with vorticity, oh my! Meanwhile, calm lakes reflect the stars, with irrotational flow that travels far.
Memory Tools
RIV - Rotational, Irrotational, Vorticity – remember these key concepts in fluid dynamics!
Acronyms
BVR - Boundary Layer, Vorticity, Rotation - key terms in fluid flow understanding.
Flash Cards
Glossary
- Rotational Flow
Fluid motion where particles exhibit rotational movement around an axis.
- Irrotational Flow
Fluid motion characterized by no rotation of particles, typically in regions far from boundaries.
- Vorticity
A measure of the local rotation of fluid particles, defined as the curl of the velocity field.
- Boundary Layer
A thin region near a surface where velocity gradients are steep and viscous effects dominate.
Reference links
Supplementary resources to enhance your learning experience.
