Vorticity and Rotationality
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Vorticity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to explore vorticity, which describes the rotation of fluid particles. Can anyone tell me why understanding this concept is crucial in fluid mechanics?

I think it's important because it helps us understand how fluids behave under different conditions.

Does it relate to how fluids create forces, like lift in airplanes?

Exactly! Vorticity plays a significant role in applications like aerodynamics. To remember this, think of the acronym 'RNA' – Rotation, Navigation, Application.

What are the signs of vorticity in a flow?

Great question! High vorticity is present in turbulent or rotational flows, which we can often visualize. Let's recap: Vorticity describes fluid rotation, it's important in mechanics, and we use 'RNA' to remember its significance.
Boundary Layers and Vorticity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s discuss boundary layers. Can anyone describe what happens as fluid flows over a surface?

I think there's a gradual change in velocity, right? It slows down at the surface.

Yes, that leads to the formation of a boundary layer.

Correct! In the boundary layer, the velocity gradient is steep, meaning vorticity is high here. Remember the phrase 'Layer of Chaos – where all the action happens.' This will help recall the significance of the boundary layer.

So the fluid above the boundary layer is irrotational?

Absolutely! Outside the boundary layer, the flow is generally irrotational. Let’s summarize: The boundary layer forms a zone of significant velocity gradient with high vorticity while the region above it remains irrotational.
Rotational vs. Irrotational Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

What is the key difference between rotational and irrotational flow?

Rotational flow has vorticity and rotation, while irrotational flow doesn't.

Can you give us practical examples of each?

Sure! A tornado represents rotational flow, while air flowing around a smooth sphere tends to be irrotational. Remember 'TORO' for tornado (rotational) and 'SPHERE' for smooth (irrotational).

This helps me visualize it better!

Fantastic! So, to recap: rotational flow has vorticity and is represented by chaotic systems like tornadoes, while irrotational flow is smooth, like airflow around spheres.
Velocity Gradients and Vorticity Measurement
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let's look at how to measure vorticity. The vorticity vector is derived from the velocity gradients. Who remembers the cross-product we use?

Is it the del operator crossed with the velocity vector?

How does that practically help us?

Excellent! It tells us how much rotation there is in the fluid. Think 'Del for Derivatives!' to remember how to find the vorticity.

Can we visualize this through a graph?

Yes! Graphs can illustrate these gradients effectively. Let’s summarize: Vorticity is obtained from the cross-product of the del operator and the velocity vector, revealing rotational behavior in fluids.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we discuss how vorticity relates to the rotational behavior of fluid particles, particularly within boundary layers. The distinction between rotational and irrotational flow is emphasized, illustrating how fluid dynamics is influenced by velocity gradients and boundary conditions.
Detailed
Vorticity and Rotationality
The section elaborates on the concepts of vorticity and rotationality in fluid mechanics, focusing on boundary layer dynamics. Vorticity, defined as the curl of the velocity field, indicates the rotational effect of the fluid particles. When a flow passes over a flat plate, viscous effects become pronounced, leading to the formation of a boundary layer where there's a significant gradient in velocity. This creates turbulence and causes fluid particles to rotate, distinguishing them from regions of irrotational flow outside the boundary layer.
As we delve deeper, we see that fluids closer to the surface experience greater velocity variations, resulting in a high vorticity zone filled with eddies or vortices. Contrastingly, outside this layer, fluid particles exhibit linear translation without significant rotation, characterizing the regions as irrotational. The equations capturing these phenomena, particularly the vorticity vector in different coordinate systems, are discussed. The section also touches upon practical applications such as the behavior of airflows around obstacles and in various fluid machines, enhancing our understanding of real-world fluid dynamics applications and computational predictions in the face of natural events like cyclones.
Youtube Videos
![What you need to know about Vorticity [Fluid Mechanics]](https://img.youtube.com/vi/Xu5IT4bL-v8/mqdefault.jpg)






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Boundary Layer Formation
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When you have a flow passing over a plate, you can anticipate a viscous effect zone known as boundary layer formations. In this zone, there is a large gradient of velocity vectors, starting from 0 to a larger value.
Detailed Explanation
In fluid mechanics, when fluid flows over a surface, it does not move uniformly. The layer of fluid that is very close to the surface experiences friction, which causes the velocity to start at zero (because the fluid is stuck to the plate) and then increase as you move away from the surface. This zone of changing velocity is called the boundary layer. The thickness of the boundary layer determines how much of the flow is influenced by the surface.
Examples & Analogies
Think of this like how a river flows over rocks. The water close to the rocks moves very slowly (almost stationary), while the water a bit further away moves much faster. This change in speed is similar to the formation of a boundary layer.
Vorticity and Rotational Flows
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In regions where there are large velocity gradients and turbulence, fluid particles will start rotating, leading to the formation of vorticity.
Detailed Explanation
Vorticity is a measure of the rotation of fluid particles in a flow. It occurs when there's a change in the velocity of the fluid across space. When fluid particles closely interact (like in a turbulent boundary layer), they may start to spin around their center of mass due to these velocity changes. This results in eddies, which are small whirlpools of fluid that contribute to the overall motion and energy dissipation in the flow.
Examples & Analogies
Imagine a bucket of water that you swirl with a stick. The water near the stick moves slower, while the water further away moves faster and starts to form swirls. Like the water, fluid particles in a boundary layer experience forces that can cause them to rotate, resulting in vorticity.
Irrotational Flow
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Outside the boundary layers, fluid particles are moving with little to no rotation. This area is referred to as the irrotational zone.
Detailed Explanation
In fluid flow, areas without vorticity exist where the fluid particles move linearly without any rotational movement. These regions are characterized by smooth flow that doesn't induce twisting among the particles. When fluid is a good distance away from surfaces or obstacles, it can be modeled as having irrotational properties, meaning the flow can be simplified greatly when analyzing it.
Examples & Analogies
Consider the flow of air in a clear sky that is far away from obstacles. The air moves smoothly and uniformly, much like how a straight line represents a path that is not disturbed by any external forces.
Understanding Vorticity vs. Angular Rotation
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
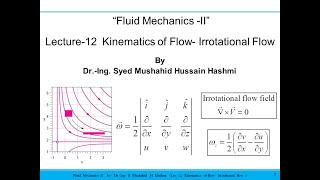
Vorticity is defined as the cross product between the gradient (del) and the velocity (V), while angular rotation refers to a different concept.
Detailed Explanation
Vorticity can be thought of as a mathematical way to describe how much a fluid is spinning at a given point, while angular rotation is more related to the overall rotation of an object. When discussing fluid dynamics, focusing on vorticity provides insights into how fluid particles interact and create complex flow patterns, such as turbulence and eddies.
Examples & Analogies
Imagine a rotating merry-go-round (angular rotation) versus a single leaf swirling in the air due to wind (vorticity). The merry-go-round has a defined center and spins around it, while the leaf's spin is more chaotic and depends on multiple local influences — akin to how vorticity works in fluid motion.
Visualizing Rotational vs. Irrotational Flow
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Visualizing figures depicting rotational and irrotational flows clarifies the difference between them.
Detailed Explanation
It’s useful to visualize flows to understand the difference between rotational flows, which exhibit spinning around an axis, and irrotational flows, where such spins are absent. Visual aids can help establish a mental image of the mechanics at play, making the concepts more tangible and accessible.
Examples & Analogies
You can think of sitting in a Ferris wheel (irrotational) — although you are moving in a circle, you aren’t spinning on your own axis — compared to going on a carousel where you're experiencing a rotation around the center (rotational). This distinction illustrates the separate behaviors of fluid flows in different contexts.
Key Concepts
-
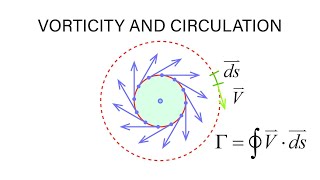
Vorticity: Indicates the rotation of fluid particles and is calculated as the curl of the velocity field.
-
Boundary Layer: A thin region near surfaces where the effects of viscosity are dominant, leading to velocity gradients.
-
Rotational Flow: A type of flow characterized by the rotation of fluid particles.
-
Irrotational Flow: Fluid flow where velocity remains constant and no particle rotation occurs.
Examples & Applications
The flow of air around an airplane wing creates vorticity that contributes to lift.
Circular water movement in a whirlpool is an example of rotational flow.
Air moving uniformly over a flat surface is an example of irrotational flow.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Vorticity spins like a wheel, in flows where chaos is real.
Stories
Imagine a rollercoaster – the irrotational track smoothly guides, while the spins and loops showcase vorticity.
Memory Tools
Remember 'VBL-RI' for Vorticity, Boundary Layer, Rotational, Irrotational.
Acronyms
Use 'RIV' for Recall
Irrotational Velocity means no rotation.
Flash Cards
Glossary
- Vorticity
A measure of the local rotation in a fluid flow, defined as the curl of the velocity vector.
- Boundary Layer
The thin layer of fluid near a solid boundary where viscous effects are significant.
- Rotational Flow
Flow in which fluid particles have angular momentum and exhibit rotation.
- Irrotational Flow
Flow where fluid particles do not experience rotation, typically characterized by a constant velocity field.
Reference links
Supplementary resources to enhance your learning experience.
