Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Boundary Layer Formation
Unlock Audio Lesson
Today, we will discuss the formation of boundary layers in fluid flows. Can anyone tell me what happens when fluid flows over a flat plate?
The fluid particles near the surface will experience friction and will move slower compared to those further away.
Exactly! This region where the velocity changes from zero to a higher value is known as the boundary layer. Remember, we typically think of it as a zone where viscous effects dominate. Can anyone explain why the velocity gradient is important here?
The large gradients lead to changes in motion, causing fluid particles to rotate.
Right. The area inside the boundary layer can lead to what we call vorticity. To remember, think 'V for Velocity, V for Viscosity.'
So in the boundary layer, there's both linear and rotational motion?
That's correct! To recap, boundary layers are thin regions where velocity transitions occur, and this difference induces rotation of the fluid particles leading to vorticity.
Irrotational vs. Rotational Flow
Unlock Audio Lesson
Now, let’s explore the difference between irrotational and rotational flows. How do we define them?
In irrotational flow, fluid particles move in straight lines without rotation.
Good point! And what about rotational flow?
In rotational flow, the particles have some rotational movement because of the vorticity present.
Exactly! Outside of the boundary layer, we can consider that the flow remains irrotational. A way to remember this is IR for 'Irrotational' means no rotation—easy to recall, right?
So, flows around objects like cylinders create rotational zones due to their influence!
Correct! To summarize, irrotational flows lack rotation, while rotational flows exhibit significant fluid particle rotation, especially near surfaces.
Understanding Vorticity
Unlock Audio Lesson
Let’s dive into vorticity now. Who can define what vorticity is?
It measures the local rotation of the fluid particles!
Exactly! Vorticity can be calculated as the cross product of the velocity gradient and the velocity vector. Can anyone think of why this math is important?
It helps us predict how fluid behaviors change in different regions, especially in turbulence.
That's spot on! To help remember, think of 'Vortex' as Vorticity. Whenever you hear rotary motions, it typically refers to vorticity.
And its value turns zero outside the boundary layer in irrotational flows?
Yes! In irrotational flow, vorticity is zero, while inside the boundary layer, it's usually non-zero. Always remember that vorticity is a key factor in understanding fluid dynamics!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore how fluid particles behave under motion and deformation, focusing on the formation of boundary layers, the presence of vorticity, and the differences between rotational and irrotational flow states. Boundary layers are defined as regions where viscous effects dominate, influencing fluid behavior significantly.
Detailed
Motion and Deformation of Fluid Particle
This section elaborates on the behavior of fluid particles under motion and deformation. The key concepts introduced include:
- Boundary Layer Formation: When a fluid flows over a surface, a boundary layer forms where there is a significant gradient of velocity vectors. This transition occurs from zero velocity at the surface to higher velocities in the main flow.
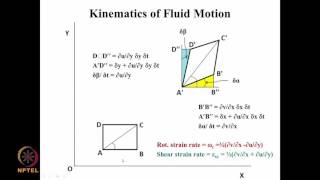
- Vorticity: In the boundary layer, there are large velocity gradients that induce rotational motion among the fluid particles, leading to vorticity, which can be mathematically defined as the cross product of the velocity gradient vector and the velocity vector.
- Rotational vs. Irrotational Flow: The section discusses the distinction between rotational flows that exhibit significant vortex formations within boundary layers and irrotational flows that occur outside these layers where no significant rotations are present.
- Vorticity in Different Coordinates: Vorticity can be expressed in both Cartesian and polar/cylindrical coordinates, accommodating two- and three-dimensional flow representations.
- Applications of Fluid Mechanics: The knowledge of fluid mechanics is crucial in real-world applications such as predicting cyclone behavior, analyzing wind velocities, and computational fluid dynamics in machinery.
Understanding these principles is essential for fluid mechanics students, as they are foundational for analyzing complex fluid flow problems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Boundary Layer Formation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When you have a flow passing over a plate, you will have a viscous effect zone called boundary layer formations. There is a zone where there is a large gradient of velocity vectors, starting from 0 to a large gradient.
Detailed Explanation
When fluid flows past a plate, it doesn't move uniformly. Near the surface of the plate, the fluid particles experience friction due to the plate's viscosity, causing them to move slower compared to those further away. This creates a boundary layer where the velocity gradient is significant. In this boundary layer, the velocity of fluid solely starts from zero at the surface to a maximum value as you move away from the plate.
Examples & Analogies
Imagine how a spoon stirs honey. Directly in contact with the spoon (the plate), the honey moves very slowly. As you move further away from the spoon, the honey can flow much more freely and quickly. This change in flow speed is akin to the boundary layer effect.
Vorticity and Rotation in Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In regions where there are large velocity gradients, fluid particles start to rotate leading to occurrences like turbulence and vorticity. The particles closer to the surface rotate, creating a complex flow with eddies.
Detailed Explanation
As fluid flows through the boundary layer and experiences large changes in velocity, the particles begin to spin or rotate, leading to a phenomenon known as vorticity. Vorticity measures how much and how fast a fluid rotates. This is important in understanding turbulence, as regions with rotation can lead to chaotic flow patterns, such as eddies and swirls.
Examples & Analogies
Think of a tornado. The winds inside a tornado are incredibly fast and they rotate around a central axis, showing high levels of vorticity. The rotation adds to the chaos of weather patterns and contributes to severe weather phenomena.
Irrotational vs Rotational Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fluid particles outside the boundary layer have zero vorticity and are classified as irrotational. Inside the boundary layers, fluid flows exhibit non-zero vorticity where rotational flows dominate.
Detailed Explanation
In fluid dynamics, flow can be classified based on whether it has rotation. Outside the boundary layers, the fluid flows straight and orderly without rotating, hence being irrotational with zero vorticity. In contrast, within the boundary layers where velocity gradients are steep, the fluid exhibits rotation and has non-zero vorticity. This distinction helps in analyzing different fluid behaviors and is crucial for understanding various flow regimes.
Examples & Analogies
A Ferris wheel represents irrotational flow: riders travel in a circular motion but do not spin in place. The wheel’s structure helps maintain this orderly motion. In contrast, the chaotic swirling of water in a fast-moving river can be seen as rotational flow, where water is spinning and creating eddies.
Measuring Vorticity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Vorticity is defined through the cross product of the gradient operator and velocity vector. It's important to differentiate it from angular velocity, as vorticity describes the local rotation of fluid elements.
Detailed Explanation
Vorticity is quantified mathematically as the curl of the velocity field, providing insight into the rotation of fluid elements. This helps engineers and scientists understand how fluids behave, especially in complex flows. It is crucial to differentiate this from angular velocity, which refers to the overall rotation of an object; vorticity focuses on localized rotational behavior within fluid dynamics.
Examples & Analogies
Imagine you have a spinning top. The angular velocity determines how fast the top spins. If you observe parts of the spinning top closely, you would find some points on its surface spinning differently due to variations in speed or direction. This local rotation is analogous to vorticity, showing how different parts of a fluid can rotate independently within the same flow.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Boundary Layer: A key region in fluid dynamics where velocity transitions occur.
-
Vorticity: A measure of the local rotational motion of fluid particles.
-
Irrotational Flow: A flow state where there is no rotation in the fluid particles.
-
Rotational Flow: A flow state characterized by the rotation of fluid particles.
-
Velocity Gradient: The spatial variation of velocity in a fluid, important in studying flow behavior.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When fluid flows past a flat plate, a boundary layer forms, creating a region where the velocity of the fluid varies significantly.
-
In a cyclonic system, air exhibits rotational flow patterns due to vorticity, while air further away may show irrotational characteristics.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the boundary layer, there's a speed affair, From zero to fast, it shows no despair.
📖 Fascinating Stories
-
Imagine a stream flowing over a flat rock. It starts at a standstill at the rock's surface but speeds up as it moves away, creating a boundary layer of varying speed.
🧠 Other Memory Gems
-
Remember 'V for Velocity, V for Viscosity' to recall that where there’s velocity change, viscosity has an impact.
🎯 Super Acronyms
B.E.V. - Boundary layer, Vorticity, Irrotational flow - remember these key concepts for fluid motion.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Boundary Layer
Definition:
A thin region adjacent to a solid boundary where the velocity of a fluid transitions from zero at the boundary to higher values in the fluid.
-
Term: Vorticity
Definition:
A vector quantity that represents the local rotation of a fluid particle, often calculated as the cross product of the velocity gradient and the velocity vector.
-
Term: Irrotational Flow
Definition:
A flow regime in which fluid particles do not exhibit rotation; characterized by zero vorticity.
-
Term: Rotational Flow
Definition:
A flow regime where fluid particles experience rotation, often associated with non-zero vorticity.
-
Term: Velocity Gradient
Definition:
The rate of change of velocity with respect to position in a fluid, important for understanding shear and vorticity.