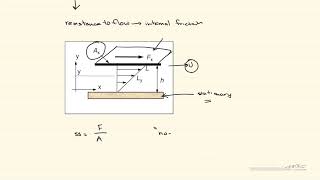
Shear Strain
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Shear Strain and Boundary Layers
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll begin our exploration of shear strain. Can anyone tell me what occurs when fluid flows over a surface?

It forms a boundary layer?

Exactly! The boundary layer is that thin region where the fluid experiences viscosity. Remember, we can use the acronym B.L.A.S.T—Boundary Layer Affects Shear Thickness—to recall its significance. Can someone describe what happens within that boundary layer?

There are velocity gradients?

Correct! These velocity gradients are crucial in determining how fluid particles move. We will discuss how they lead to rotations and ultimately to the formation of eddies.
Understanding Vorticity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's talk about vorticity. Who can explain what vorticity measures in a fluid?

It's the measure of rotation of fluid particles, right?

Exactly! Vorticity tells us about the rotational motion of particles. It's quantified as the curl of the velocity vector. Remember the mnemonic C.U.R.L to recall what vorticity represents. What would you say happens when we have a non-zero vorticity?

That indicates a rotational flow!

Right! And in contrast, in regions of zero vorticity, we have irrotational flow. This distinction is crucial in fluid dynamics. Can anyone give an example of a situation with irrotational flow?

The flow far away from any objects, like in the middle of a calm lake?
Applications and Relevance of Shear Strain and Vorticity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

We'll now explore where these concepts apply in the real world. How does understanding shear strain and vorticity help engineers, for example?

It's important for designing more efficient machines, like turbines!

Absolutely! The performance of turbo machinery largely depends on managing boundary layers. Remember the A.C.T acronym—Analyze, Control, Test—to keep this in mind. Can anyone think of a specific scenario where predicting vorticity might be crucial?

Forecasting weather patterns?

Spot on! In meteorology, understanding vorticity is essential in predicting cyclones and other weather phenomena.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Focusing on shear strain and its relationship with boundary layer formation, the section examines how velocity gradients impact fluid particle movement, leading to rotational and irrotational flow. Additionally, the section clarifies the distinction between vorticity and angular velocity.
Detailed
Detailed Summary of Shear Strain
In fluid mechanics, shear strain is crucial for understanding how fluids behave under different stress conditions. When fluids flow over surfaces, a boundary layer is formed where viscosity predominates. Within this boundary layer, large velocity gradients create conditions that lead to the rotation of fluid particles, resulting in phenomena such as eddies.
Key aspects covered include:
- Boundary Layer Formation: This thin region near surfaces has significant velocity variations and viscous effects.
- Vorticity: Defined as the curl of the velocity field, it indicates how fluid particles rotate. Outside the boundary layer, fluid is irrotational, while inside, it shows rotational flow.
- Applications: Understanding these concepts is essential in predicting and analyzing flow behaviors in various engineering applications, including turbo machinery and flow around objects.
The section also differentiates between vorticity (which can be observed and quantified) and angular velocity (which relates to rotation), helping to clarify common misconceptions. This understanding is foundational for more advanced studies in fluid mechanics and computational fluid dynamics.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Shear Strain
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When you have a flow passing over a plate, you can anticipate the formation of a viscous effect zone known as the boundary layer. In this zone, there is a large gradient of velocity, starting from 0 and reaching a significant value. This gradient causes fluid particles to rotate rather than move in a straight line.
Detailed Explanation
This chunk introduces the concept of shear strain, focusing on how fluid flow over a surface leads to the formation of a boundary layer. The boundary layer is significant because it is where the effects of viscosity dominate due to the velocity gradient present. The phrase 'large gradient of velocity' means that as you move from the plate's surface to the fluid's exterior, the velocity changes rapidly, causing particles near the surface to rotate.
Examples & Analogies
Imagine stirring a thick soup with a spoon. The soup close to the spoon (the plate) moves slowly, while the soup farther away moves more quickly. This gradient of speed causes some of the soup particles to get caught in a swirling motion, resembling the concept of the boundary layer.
Vorticity in Boundary Layers
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In boundary layers, large velocity gradients induce fluid particle rotations, leading to the formation of eddies. Outside of the boundary layer, the fluid is described as irrotational, where particles move without rotation.
Detailed Explanation
This chunk focuses on the vorticity within boundary layers. Vorticity refers to the amount and direction of fluid rotation. Inside the boundary layer, the high velocity gradients cause particles to experience turbulence and create small whirlpools, or eddies, due to the rotation. In contrast, outside this layer, the flow is irrotational, which means the particles do not exhibit rotational behavior as they travel in a linear path.
Examples & Analogies
Consider a river flowing over rocks. Near the surface (the boundary layer), you see water swirling around the rocks, creating tiny whirlpools (eddies), whereas farther downstream, the water flows smoothly and straight without rotation (irrotational flow).
Understanding Vorticity and Rotation
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
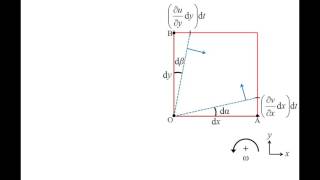
The relationship between vorticity and angular rotation is important. Vorticity is defined as the cross product of the gradient and the velocity vector. Understanding this distinction helps in analyzing fluid motion.
Detailed Explanation
This chunk emphasizes the mathematical relationship between vorticity and angular rotation, helping to differentiate the two concepts. Vorticity provides a measure of rotation of fluid elements and is calculated using vector calculus. While vorticity can suggest rotational behavior of the fluid, angular rotation is a specific motion that can be assessed separately.
Examples & Analogies
Think of a whirlpool in a sink. The vorticity is like the strength of the whirlpool (how fast the water spins), while the angular rotation would tell you the direction and rate of that spin. Both concepts relate to fluid movement but describe different aspects of that movement.
Irrotational vs Rotational Flow
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Fluid particles outside the boundary layer exhibit zero vorticity, making them irrotational. Conversely, inside the boundary layers, the fluid demonstrates non-zero vorticity, indicating rotational flow.
Detailed Explanation
In this chunk, the distinction between irrotational and rotational flow is clarified. Outside the boundary layer, where the fluid is free from obstructions, the movement is smooth, leading to zero vorticity. However, as the flow enters the boundary layer where viscous effects are relevant, the particles begin to rotate, thus exhibiting vorticity. This is essential for understanding the behavior of fluids in various engineering applications.
Examples & Analogies
Consider a spinning top. If you observe the top while it’s spinning (rotational zone), you see it move in circles. Now, if you look at the air around it (irrotational zone), it flows without any rotation, creating a simple, smooth movement as it moves away from the top.
Vorticity in Different Coordinate Systems
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Vorticity can also be expressed in different coordinate systems such as Cartesian and polar coordinates, allowing for its analysis in both 2D and 3D flows.
Detailed Explanation
This chunk discusses how vorticity is represented in different mathematical frameworks, making it applicable to various fluid dynamics scenarios. In a 2D flow, vorticity simplifies to components that are easy to calculate. For 3D flows, incorporating cylindrical or polar coordinates allows for more complex fluid behaviors to be analyzed, facilitating understanding in different practical situations.
Examples & Analogies
Think of how you may navigate a city. In flat areas, using a simple map (Cartesian coordinates) works well. However, in hilly terrains or areas with curves, a specialized road map (polar coordinates) helps you find routes more effectively. Likewise, analyzing fluid dynamics sometimes requires different mathematical tools depending on the situation.
Key Concepts
-
Shear Strain: Deformation due to shear stress without volume change.
-
Boundary Layer: Region where fluid experiences significant viscosity effects.
-
Vorticity: Quantity that describes the rotation of fluid particles.
-
Irrotational Flow: Movement where fluid particles do not exhibit rotational motion.
-
Rotational Flow: Flow characterized by the rotation of fluid elements.
Examples & Applications
The formation of eddies in riverbeds due to varying flow conditions and obstacles.
The behavior of air around an airplane wing, illustrating boundary layers and vorticity.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a flow so calm and still, vorticity brings the thrill, rotation found in eddy's swirl, while boundary layers dance and twirl.
Stories
Imagine a river flowing gently, where rocks peek from beneath. The calm waters gliding by represent irrotational flow, while the whirlpools forming near the rocks express vorticity in action!
Memory Tools
V.E.R.B. for remembering Vorticity: Velocity, Edges, Rotational motion, and Boundary layers.
Acronyms
B.L.A.S.T. to remember Boundary Layer Affects Shear Thickness.
Flash Cards
Glossary
- Shear Strain
The deformation of a material due to shear stress, leading to a change in shape without affecting volume.
- Boundary Layer
The thin region in a fluid near the surface where viscous effects are significant and where velocity gradients occur.
- Vorticity
A measure of the local rotation of fluid elements in flow, calculated as the curl of the velocity vector.
- Irrotational Flow
Flow in which the fluid elements do not rotate about their center of mass.
- Rotational Flow
Flow in which the fluid elements have a rotational motion.
Reference links
Supplementary resources to enhance your learning experience.
