Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Boundary Layers
Unlock Audio Lesson
Good morning everyone! Today we will discuss boundary layer theory. Can anyone tell me what a boundary layer is?
Isn't it the area where the fluid's velocity changes from zero at the surface to the free stream velocity?
Exactly! The boundary layer forms due to the no-slip condition at solid surfaces. Remember, the thickness of this layer varies depending on the flow conditions.
What's the significance of knowing the boundary layer thickness?
Good question! Knowing the boundary layer thickness helps us understand drag forces, skin friction, and flow characteristics around structures.
So how does the Reynolds number factor into this?
Great point! The Reynolds number helps determine the nature of the flow. If it's less than 10^5, the flow is typically laminar, while above 3×10^6 indicates turbulent flow.
To remember this: 'LRT' - Laminar is less Than 10^5 and Turbulent is above 3×10^6!
In summary, the boundary layer is crucial for analyzing flow dynamics and reducing drag. Let's move on to the next topic!
Assumptions in Boundary Layer Theory
Unlock Audio Lesson
Now, let's dive into the assumptions that underpin the boundary layer equations. What do you think is the first assumption?
Maybe that we're working under steady flow conditions?
Correct! Steady flow implies the fluid properties at a point do not change with time, which simplifies our analysis significantly.
Are we also ignoring gravity effects?
Exactly! In a thin boundary layer, inertia forces overshadow gravity, enabling us to neglect it.
How do we ensure that we are focusing on the right terms in the equations?
We use dimensional analysis! By non-dimensionalizing our equations, we can identify which terms are significant and simplify the equations accordingly.
To help remember this, think 'FINE' - Flow is steady, Inertia dominates over gravity, Non-dimensionalization is key, and Evaluate assumptions!
So, in summary, these assumptions streamline the derivation of the boundary layer equations from the Navier-Stokes equations.
Pressure Gradients in Boundary Layers
Unlock Audio Lesson
Next, let's talk about pressure gradients in the boundary layer. How are they treated in our analysis?
Are they considered uniform across the thickness?
Yes! In the boundary layer approximation, we assume the pressure does not change across the thickness, making it almost constant.
So, does that mean if we vary the pressure only in the x-direction?
That's right! We conclude the pressure gradient in the y-direction is negligible, simplifying our equations further.
How does this relate to calculating drag forces on surfaces?
Understanding pressure gradient effects is fundamental in finding drag forces, as they directly affect the flow behavior near surfaces.
To recap, we find pressure gradients constant in the y-direction helps us simplify our equations and focus on shear forces instead.
Practical Applications of Boundary Layer Theory
Unlock Audio Lesson
To wrap up our discussion, how do engineers utilize boundary layer theory in real-world applications?
It must help design vehicles? Knowing boundary layers helps reduce drag!
Exactly! Designers optimize shapes to minimize drag using boundary layer principles.
Do we also use it for structures like buildings?
Yes! Understanding airflow around structures leads to better ventilation and durability.
So, from aircraft to buildings, these concepts are truly vital?
Absolutely! Their practical importance cannot be overstated, which is why we study them so thoroughly.
Today, we reviewed boundary layers, assumptions, pressure gradients, and practical applications. Keep these concepts in mind for your future projects!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section highlights the foundational assumptions that lead to the derivation of boundary layer equations from the Navier-Stokes equations, emphasizing the laminar flow characteristics, Reynolds number significance, and the simplifications made in analysis. It also explores the engineering relevance of these concepts.
Detailed
Assumptions Behind Boundary Layer Equations
In fluid mechanics, boundary layer theory is vital for understanding flows near solid surfaces. The assumptions behind boundary layer equations simplify the analysis of the complex Navier-Stokes equations. Here are the key aspects discussed:
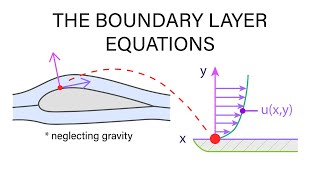
- Boundary Layer Concept: The boundary layer forms when fluid flows past a solid object, leading to varying velocity profiles. The layer has thickness defined by where the flow velocity approaches the free stream velocity.
- Laminar vs. Turbulent Flow: The transition of flow behavior from laminar (for Reynolds numbers less than 10^5) to turbulence (greater than 3×10^6) is crucial for deriving boundary layer characteristics.
- Steady Flow Assumption: The analysis often assumes steady flow, simplifying equations by neglecting unsteady terms.
- Neglect of Gravity Forces: Gravity effects are usually small compared to inertial forces within thin boundary layers, allowing for their neglect in most cases.
- Dimensional Analysis and Non-Dimensionalization: Key to the simplification process is normalization of variables to determine which terms are significant, based on their order of magnitude. This leads to the conclusion that in boundary layers, pressure gradients are nearly constant, allowing the focus on shear stresses and flow dynamics.
This foundational knowledge allows engineers to calculate important parameters like wall shear stress and flow separation, instrumental in designing various structures like aircraft and automobiles.
Youtube Videos
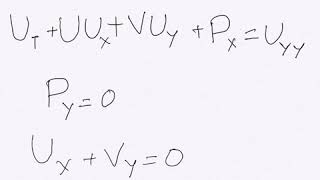
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Boundary Layers and Their Importance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Today, I will talk about boundary layer equations, which are approximations of the basic Navier-Stokes equations. It is essential to understand the utility of boundary layers in fluid mechanics, as it helps calculate wall shear stress and approximates flow behavior near surfaces.
Detailed Explanation
The boundary layer concept helps simplify the analysis of fluid flow past surfaces, such as flat plates or airfoils. Since fluids are viscous, the interaction between the fluid and solid surfaces affects the flow. By focusing on the boundary layer, which is the thin region near the surface where the effects of viscosity are significant, we can approximate the flow conditions without complex calculations involving the entire flow field.
Examples & Analogies
Think of a boundary layer like a thin layer of jam spread on a piece of toast. The jam sticks closely to the surface, just as the fluid's behavior near the surface is influenced heavily by viscosity. If you’re trying to evaluate how the jam affects the taste (similar to how we analyze fluid flow), it helps to understand only that sticky layer rather than the whole jar of jam.
Establishing the Flow Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In our analysis, we assume a steady flow regime. The local accelerations and gravitational forces are neglected in the boundary layer equations, focusing primarily on the viscous effects within the flow.
Detailed Explanation
Assuming steady flow simplifies the equations significantly. Without localized changes in velocity or elevation (gravity) affecting our calculations, we can concentrate on the critical factors like viscous forces acting in the boundary layer. This means we don't consider how the flow might change with time, allowing us to derive simpler equations.
Examples & Analogies
Imagine driving in a steady car on a highway. If you think about every bump and dip on the road, you could easily get distracted and confused. Instead, if you keep a steady speed, you can focus on the journey rather than the little changes in elevation, similar to how we simplify our focus to the effective factors in boundary layer analysis.
Order of Magnitude Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We conduct an order of magnitude analysis to determine which terms in the Navier-Stokes equations dominate and which can be neglected. This helps in simplifying our boundary layer equations.
Detailed Explanation
This analysis involves comparing the sizes (magnitudes) of different physical quantities, like velocity, pressure, and viscosity, to identify which influences the behavior of the flow most significantly. By understanding the relative sizes of these terms, we can simplify the equations, removing less significant factors and focusing on those that substantially affect the flow.
Examples & Analogies
Consider preparing a recipe. If you're making a giant cake but only have a tiny pinch of salt compared to the massive amount of flour and sugar, you can ignore the salt's impact while focusing on the more substantial ingredients. This is similar to how we assess which terms in our flow equations can be neglected based on their significance.
Neglecting Non-Dominant Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the boundary layer, the pressure gradient across the layer is treated as negligible, indicating that pressure does not change significantly across the thickness of the layer.
Detailed Explanation
We posit that within the thin boundary layer, pressure remains approximately constant. This assumption stems from the observations that any variations in pressure across the layer don’t have considerable effects on the calculations of shear stress and velocity. Thus, for most analytical purposes, this simplification holds true.
Examples & Analogies
If you think of a dense crowd at a concert where the majority of people are tightly packed in one area, the pressure felt by someone in the crowd won’t change dramatically irrespective of where they are standing because everyone is shoved together. Likewise, in our boundary layers, pressure remains quite constant across its thickness.
Conclusion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Overall, the assumptions behind boundary layer equations, such as neglecting gravity and local accelerations, allow scientists and engineers to simplify fluid flow analysis effectively.
Detailed Explanation
By focusing on these simplified assumptions, we can derive useful equations that yield significant results for practical applications in engineering, thereby making complex fluid dynamics manageable. These approximations are pivotal for developing tools in computational fluid dynamics that engineers can use in various designs.
Examples & Analogies
It’s like using a simplified map when navigating a complex city. Instead of getting lost in every street detail, the simplified map highlights major routes, making it easier to plan your trip efficiently. In fluid mechanics, boundary layer assumptions similarly help us navigate the complexity of fluid flows.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Boundary Layer: The fluid layer affected by viscosity near a solid surface.
-
Reynolds Number: A dimensionless number indicating flow characteristics.
-
Steady Flow: Assumption that fluid properties remain constant with time.
-
No-Slip Condition: Fluid velocity at the surface is equal to that of the surface.
-
Pressure Gradient: The rate at which pressure changes in a fluid.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When analyzing airflow over an airplane wing, the boundary layer helps predict lift and drag.
-
In designing vehicles, engineers consider boundary layer effects to improve fuel efficiency and performance.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Boundary layers form despite the tide, where viscosity and forces collide.
📖 Fascinating Stories
-
Imagine a river flowing smoothly over a rock. Near the rock, the water slows down—this is the boundary layer, creating a peaceful zone where forces interact.
🧠 Other Memory Gems
-
Remember 'B-N-P' for Boundary Layer: No-Slip Condition and Pressure Gradient focus!
🎯 Super Acronyms
Use ‘B-L-A-P’ to recall Boundary Layer, Assumptions, Laminar versus Turbulent, Pressure Gradient.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Boundary Layer
Definition:
The layer of fluid in the immediate vicinity of a bounding surface where the effects of viscosity are significant.
-
Term: Laminar Flow
Definition:
A flow regime characterized by smooth and orderly fluid motion, typically occurring at low Reynolds numbers.
-
Term: Turbulent Flow
Definition:
A chaotic flow regime characterized by vortices, eddies, and apparent randomness, typically at high Reynolds numbers.
-
Term: Reynolds Number
Definition:
A dimensionless quantity that measures the ratio of inertial forces to viscous forces within a fluid, indicating flow regime.
-
Term: NoSlip Condition
Definition:
The condition at the boundary where the fluid velocity is equal to the boundary surface velocity, leading to zero relative velocity.
-
Term: Pressure Gradient
Definition:
Change in pressure per unit distance in a direction within a fluid medium.