Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introductory Concepts of Boundary Layers
Unlock Audio Lesson
Good morning, everyone! Today we'll explore boundary layers in fluid mechanics. Can anyone start by explaining what a boundary layer is?
A boundary layer is a thin region near a solid surface where the flow velocity changes from zero to the free stream velocity.
Exactly! The concept is crucial for understanding how fluids interact with surfaces. Remember, the 'no-slip condition' means that fluid at the surface is stationary while the flow velocity increases away from the surface.
Isn't there a difference in behavior between laminar and turbulent boundary layers?
Great question! Laminar boundary layers are smooth and orderly, while turbulent layers are chaotic and have higher mixing. We'll see how these affect drag forces.
Let’s summarize this session: boundary layers are critical in fluid flow analysis, affecting velocity profiles and shear stresses. Keep these differences in mind as we proceed!
Calculating Boundary Layer Properties
Unlock Audio Lesson
Now that we understand boundary layers, let's discuss how CFD helps in calculating properties like boundary layer thickness and shear stress. What do we use for this calculation?
We can use boundary layer equations derived from the Navier-Stokes equations.
Correct! These approximations allow us to simplify complex flows. Can anyone recall the conditions required for applying these equations?
They assume that the flow is steady and incompressible.
Exactly! CFD tools take those assumptions and allow us to visualize and compute these parameters much more effectively than traditional methods. Remember the acronym 'STI' for Steady, Two-dimensional, and Incompressible!
To recap, CFD tools allow for the direct analysis of boundary layer properties under assumed conditions, vastly improving efficiency and accuracy.
CFD Historical Context and Development
Unlock Audio Lesson
Let’s shift gears a bit. Can anyone tell me how computational technologies have changed our approach to fluid dynamics over the years?
A long time ago, we needed to rely heavily on complex mathematical techniques, but now we have computers that do a lot of that heavy lifting for us.
Exactly! CFD has become a game changer. It allows engineers to simulate real-world scenarios more accurately and quickly. Why do you think that’s important?
It helps in reducing design times and costs, and we can easily visualize flow patterns!
Spot on! Simulation tools are crucial in modern engineering. So today, we no longer just approximate mathematically but evaluate using computational techniques which reflects real-life scenarios better.
To summarize, the evolution from mathematical techniques to CFD has revolutionized fluid analysis, leading to faster and more accurate designs.
Application of Boundary Layers in Engineering Solutions
Unlock Audio Lesson
Let’s discuss some real-world applications. How can understanding boundary layers affect engineering design in vehicles?
It helps determine drag forces which affect fuel efficiency in cars and planes.
Correct! Designers need to pay close attention to how boundary layers behave at high speeds. When we design automotive bodies, we want to minimize drag, right?
Yes, and CFD lets us test different designs quickly without needing to build models first.
Exactly! CFD allows for rapid prototyping in design, enabling engineers to optimize shapes that reduce drag. This is a perfect case of where science meets application.
In summary, understanding boundary layers is critical in engineering design, enhancing efficiency and performance in vehicles.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section focuses on the introduction of Computational Fluid Dynamics (CFD) as a significant tool in the field of fluid mechanics. It elaborates on the boundary layer approximations, their historical context, and how CFD tools enable complex fluid flow analysis without extensive mathematical approximations that were previously necessary.
Detailed
Detailed Summary
This section provides a comprehensive overview of the Utilization of Computational Fluid Dynamics (CFD) in fluid mechanics, specifically in relation to boundary layer approximations.
The concept of boundary layers plays a crucial role in understanding fluid flow over surfaces and is foundational in solving Navier-Stokes equations. The section begins by noting the importance of CFD tools that have emerged, facilitating accurate fluid flow simulations that were previously reliant on cumbersome mathematical approximations.
Key aspects covered include:
1. Boundary Layer Concept: Understanding boundary layers in fluid dynamics is essential for analyzing how fluids behave around objects, including laminar and turbulent flows.
2. Historical Context: The development of computational tools has significantly changed how boundary layer problems are approached compared to traditional methods employed 70-80 years ago.
3. CFD Applications: It elaborates on the ways CFD can simplify and solve complex fluid dynamics problems, providing practical applications in engineering and design.
4. Boundary Layer Equations: The section covers boundary layer equations derived from the Navier-Stokes equations, emphasizing their role in predicting shear stress and thickness in laminar flow conditions.
The implications of these concepts on engineering practices, especially in designing vehicles and structures subject to fluid flow, underscore the significance of CFD as a revolutionary approach in fluid dynamics.
Youtube Videos
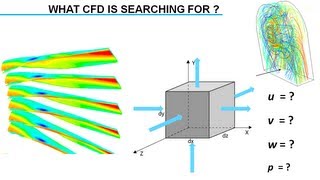
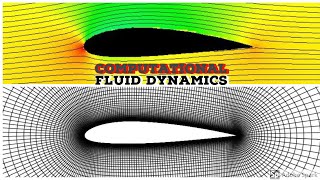
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Boundary Layers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We used to do it almost 70 to 80 years back when there was no the computational facilities what today we have. So looking that I will just going through this Senzel Cimbala books which giving a lot of illustrations about the boundary layers and partly we looking it FM White book but as I said it that we are looking it you should try to understand what is a boundary layer concept not going more details about the mathematical formulations, how we do the approximations for different conditions because that itself is in advanced level of the fluid mechanics.
Detailed Explanation
This chunk explains the historical context of boundary layer theory and its development over the past decades. Initially, before the advent of modern computational tools, engineers had to rely on analytical approximations to understand boundary layers. However, with the introduction of Computational Fluid Dynamics (CFD), many of these approximations have become unnecessary, allowing for more accurate modeling and understanding of fluid behaviors around objects. The text emphasizes that while advanced mathematical formulations exist, the focus here is on understanding the fundamental concepts of boundary layers.
Examples & Analogies
Think about how we used to navigate using physical maps. It required significant skill and understanding of geography to read distances and directions. With the advent of GPS, navigation has become straightforward, similar to how CFD simplifies the complex calculations of fluid dynamics that once required painstaking analytical methods.
Understanding Boundary Layer Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So today I talk about boundary layer equations which is a approximations of the basic Navier-Stokes equations okay. That is what today with figures, with the sketches, with the approximations that what we will derive it.
Detailed Explanation
In this section, the narrator introduces boundary layer equations, derived from the basic Navier-Stokes equations, which govern fluid motion. The boundary layer equations simplify complex fluid dynamics problems by focusing on the thin layer of fluid right near a surface, where effects such as viscosity are significant. The speaker plans to illustrate these concepts via diagrams and sketches, enhancing the learning experience by providing visual context to the equations and their derivations.
Examples & Analogies
Imagine standing next to a flowing river. The water closest to the bank moves slowly due to friction with the land, while the water in the middle flows quickly. The equations that describe this slow-moving layer of water along the river bank are akin to the boundary layer equations used in fluid dynamics—focusing on how properties change near the surface.
Reynolds Numbers and Flow Characteristics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If Reynolds number x is less than 10 to the power 5... Reynolds number greater than 3 into 10 to the power 6 is 3 millions okay then the flow will be the turbulent.
Detailed Explanation
This chunk delves into the concept of Reynolds numbers, which are crucial in characterizing fluid flow conditions. The speaker describes how flow transitions from laminar to turbulent based on the value of the Reynolds number—a dimensionless number representing the ratio of inertial forces to viscous forces in a fluid. At lower Reynolds numbers (less than 100,000), the flow is laminar (smooth and orderly), while at higher values (greater than 3,000,000), turbulence appears, resulting in chaotic flow patterns. This understanding is vital for predicting flow behavior around objects.
Examples & Analogies
Consider riding a bicycle through water. At low speeds, the water flows smoothly around you, representing laminar flow. As you speed up, the water starts splashing and swirling around, mimicking turbulent flow, showcasing how the dynamics change based on speed, similar to how Reynolds numbers dictate flow behavior in different scenarios.
Application of CFD in Boundary Layer Studies
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So today we have a lot of computational fluid dynamics tools which we can solve the full Navier-Stokes equations.
Detailed Explanation
This section highlights the role of computational tools in modern fluid dynamics. Today, various CFD tools allow engineers and scientists to simulate fluid flows accurately without having to rely solely on analytical solutions. These simulations provide insights into how fluids behave around different geometries and conditions, facilitating better designs in engineering applications. The ability to visualize these flows through advanced software has transformed the field, making it possible to handle complex real-world scenarios that would have been extremely difficult to analyze manually in the past.
Examples & Analogies
Imagine you are designing a new car. Instead of building and testing physical prototypes, you can use CFD software to simulate how air flows around the car's shape, allowing you to tweak the design for optimal aerodynamic performance before the first model is even built—much like using a flight simulator to practice flying before getting into an actual airplane.
Conclusion and Future Directions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus when you apply it you are getting the velocity u free stream velocity plus del square y.
Detailed Explanation
In concluding this section, the speaker emphasizes the importance of boundary layer equations derived from Bernoulli's principle and how they allow for practical applications in flow problems. These equations lead to further studies on drag, pressure distribution, and flow separation, crucial for engineers. The discussion also hints at future learning about more complex flow scenarios such as turbulent flows and how CFD can continue to evolve in this realm, preparing students for advanced topics in fluid mechanics.
Examples & Analogies
Consider a gardener designing a new irrigation system. After initially using simple equations to predict water flow, they might turn to sophisticated modeling software to understand complex interactions in their garden’s unique design. This progression symbolizes the journey of a fluid dynamics student from basic principles to advanced applications in real-world settings.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Boundary Layer: The zone near a solid surface where flow velocity transitions.
-
CFD: A method for solving complex fluid dynamics problems using computational tools.
-
Laminar vs. Turbulent Flow: Different flow patterns; laminar is smooth while turbulent is chaotic.
-
Navier-Stokes Equations: Governing equations for fluid motion that account for viscosity.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The flow of air over an airplane wing involves boundary layer analysis to minimize drag and improve fuel efficiency.
-
In car design, CFD is employed to optimize the shape of the vehicle to reduce air resistance, showcasing the importance of boundary layer behavior.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a layer close to a plate, the fluid waits, flows not straight, from zero up to speed it does grow, that’s where the boundary layer will show.
📖 Fascinating Stories
-
Imagine a smooth road. As cars (fluids) approach a barrier (surface), they slow down until they reach the speed limit (free stream velocity). This journey forms a boundary layer, crucial for understanding car designs.
🧠 Other Memory Gems
-
Remember 'B-C-F-R': B for Boundary layer, C for CFD, F for Flow types (laminar and turbulent), R for Reynolds number relevant to flow.
🎯 Super Acronyms
Use the acronym 'BLAST' to recall key boundary layer concepts
- B: for Boundary
- L: for Layer
- A: for Analysis
- S: for Shear Stress
- T: for Turbulence.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Boundary Layer
Definition:
A thin region adjacent to a solid surface where the flow velocity transitions from zero to the free stream velocity.
-
Term: NavierStokes Equations
Definition:
A set of equations describing how the velocity field of a fluid evolves over time considering viscosity.
-
Term: Laminar Flow
Definition:
A smooth and orderly flow regime characterized by parallel layers of fluid.
-
Term: Turbulent Flow
Definition:
A chaotic and irregular flow regime characterized by rapid fluctuations and mixing.
-
Term: CFD (Computational Fluid Dynamics)
Definition:
The use of numerical analysis and algorithms to solve and analyze fluid dynamics problems.