Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Boundary Layers
Unlock Audio Lesson
Good morning, class! Today we're diving into the concept of boundary layers in fluid flow. Can anyone tell me what they understand about the term 'boundary layer'?
Isn’t it the thin layer of fluid near a surface where the flow velocity changes?
Exactly! The boundary layer is indeed a thin region adjacent to a surface where viscosity affects the flow. Remember, it separates the flow into two zones: the boundary layer and the free stream. To help remember, think of 'B.L.' for 'Boundary Layer.'
Why do we care about this layer?
Great question! It's essential in determining the drag and lift forces on objects like wings or cars. The behavior of fluid flow changes significantly across this boundary layer.
What affects the thickness of this boundary layer?
The thickness is influenced primarily by the Reynolds number. As the Reynolds number increases, the boundary layer thickness decreases. Just remember: higher Reynolds number, thinner boundary layer. That’s our mnemonic: 'Big R, Skinny B.'
Does that mean we can control flow behavior?
Absolutely! By manipulating designs, we can influence the Reynolds number and thus manage boundary layer thickness. Let's move on to those calculations!
In summary, boundary layers are critical for understanding fluid dynamics around surfaces, influencing drag and lift, and dependent on the Reynolds number. Thank you for your input!
Reynolds Number and Flow Types
Unlock Audio Lesson
Let’s talk about the Reynolds number and its importance. Student_1, could you remind us what it is?
Isn't it the ratio of inertial forces to viscous forces in fluid flow?
Right! It helps determine whether flow is laminar or turbulent. Can anyone tell me the typical threshold values for transitions?
If the Reynolds number is less than 100,000, the flow remains laminar, and above that is turbulent.
Perfect! To recall: '100K for Laminar to Turbulent Transformation.' That's our reference point. So, how does this relate back to the boundary layer?
It would affect the flow behavior and the thickness of the boundary layer, right?
Exactly! And turbulent boundary layers are usually thicker, leading to increased drag. Thus, controlling the Reynolds number is crucial in engineering.
So, how do we manage these effects in real-world applications?
Great follow-up! Techniques like shape optimization, adding vortex generators, or controlling surface roughness can help manage flow behaviors. Remember, managing the flow is key in design!
In summary, the Reynolds number is vital for determining flow types, affecting boundary layer characteristics and engineering applications.
Deriving Boundary Layer Equations
Unlock Audio Lesson
Now let's delve into derivation. Who can remind me what the Navier-Stokes equations govern? Student_1?
They describe the motion of fluid substances, right?
Exactly! Now, when we're considering boundary layers, we simplify these equations. Can someone explain what assumptions we make to derive the boundary layer equations?
We usually assume steady flow, ignore gravity, and consider the flow to be incompressible?
Spot on! These assumptions lead us to simplified forms of the equations. Let's not forget that we also do an order of magnitude analysis to drop insignificant terms, making our analysis more manageable.
And that helps us focus on dominant forces affecting the flow, right?
Exactly! The important terms are what drive velocity and pressure changes. Keep in mind that ignoring too many terms would lead us back to the Euler equations, which aren't valid here.
What do we end up with after all these simplifications?
We derive the boundary layer equations, essential for fluid flow calculations. This gives us a framework for analyzing flows around various shapes and how they interact with the boundary layer.
Let's recap: We simplify Navier-Stokes by using certain assumptions, focus on significant terms, and end up with the boundary layer equations that are crucial for practical applications in fluid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, students explore the concept of boundary layers in fluid mechanics using the boundary layer equations derived from the Navier-Stokes equations. Key points include understanding laminar and turbulent flow conditions as determined by the Reynolds number, the significance of boundary layer thickness, and the impact of flow separations on fluid behavior.
Detailed
Detailed Summary
In this section of the fluid mechanics course, the concept of boundary layers is introduced as a fundamental aspect of fluid dynamics, particularly when dealing with flow past objects. The discussion highlights the methods of simplifying Navier-Stokes equations to obtain boundary layer equations, leveraging the assumptions of laminar flow and the implications of the Reynolds number in understanding the flow regime.
The following key points are discussed:
- Boundary Layer Concept: The boundary layer is a thin layer of fluid in close proximity to a surface where the effects of viscosity are significant, leading to variations in velocity. At the edge of this layer, the flow transitions to the free stream velocity.
- Reynolds Number: The Reynolds number (Re) serves as a critical parameter to distinguish between laminar flow (Re < 10^5), transitional flow (between laminar and turbulent), and fully turbulent flow (Re > 10^6). Laminar boundary layers are thinner, while turbulent layers are thicker.
- Boundary Layer Thickness: Defined as the distance from the surface to a point where the flow velocity reaches about 99% of the free stream velocity. As Reynolds number increases, boundary layer thickness decreases.
- Flow Separations: Understanding flow separation is crucial as it disrupts the boundary layer and results in wake formations, impacting drag and lift forces on objects like airfoils.
- Mathematical Derivation: The section includes the derivation of boundary layer equations from Navier-Stokes equations through techniques like order of magnitude analysis and dimensional analysis, focusing on eliminating less significant terms.
- Practical Relevance: Practical applications in engineering (e.g., in designing vehicles and aircraft) necessitate understanding these layers to optimize performance and reduce drag.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Boundary Layers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In today’s lecture, we introduce boundary layer equations as approximations of the basic Navier-Stokes equations. We discuss how to derive these equations with illustrations and the combinations of Euler equations and boundary layer equations needed for laminar flow solutions.
Detailed Explanation
This chunk establishes the fundamental context of boundary layer concepts in fluid mechanics. It states that boundary layer equations simplify the complex Navier-Stokes equations, which describe fluid motion. We will illustrate how these equations relate to laminar flows, where the fluid is smooth and orderly, opposed to turbulent flows where it is chaotic. The combination of Euler and boundary layer equations will help in deriving the boundary layer equations for practical applications.
Examples & Analogies
Think of a river (fluid) flowing over rocks (object). Near the rocks, the water flows more slowly compared to further out in the river. The region where the water stops immediately against the rock and where it gradually speeds up is akin to the concept of a boundary layer.
Understanding Reynolds Number
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Reynolds number, defined as (rho V x) / mu, helps categorize flow regimes. For Reynolds numbers less than 10^5, the flow remains laminar, while values greater than 3×10^6 indicate a turbulent flow.
Detailed Explanation
The Reynolds number quantifies whether a flow is laminar or turbulent. It's calculated using the fluid's density, average velocity, characteristic length, and viscosity. A lower Reynolds number indicates smoother flow (laminar), whereas higher numbers show chaotic flow patterns (turbulence). Understanding this classification is crucial for analyzing fluid behavior around surfaces such as wings or plates.
Examples & Analogies
Imagine driving on a smooth straight highway versus a winding mountain road. On the highway (laminar flow), your car moves steadily with little effort. On the mountain road (turbulent flow), there are twists and turns, creating more chaotic movement. The Reynolds number helps us understand these driving conditions in terms of fluid flow.
Boundary Layer Thickness
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Boundary layer thickness is the distance from the wall where the flow velocity reaches approximately 99% of the free stream velocity. This thickness decreases with increasing Reynolds numbers and can be measured in wind tunnels or through computational fluid dynamics (CFD).
Detailed Explanation
Boundary layer thickness is a critical concept, representing the transition from a no-slip condition at a solid surface to nearly full velocity away from the surface. As Reynolds numbers increase, the boundary layer becomes thinner, which implies more efficient flow over surfaces, leading to lower drag forces in applications such as aircraft design.
Examples & Analogies
Consider an ice skater spinning. When they pull their arms in closer, they spin faster and with less resistance from the air around them. In a similar way, as the boundary layer thickness decreases, the drag on the object also decreases, improving performance.
Pressure Gradient in Boundary Layers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In boundary layers, the pressure gradient across the layer is nearly zero, indicating that pressure remains constant throughout the thin layer. This constant pressure enables simplified calculations in boundary layer analysis, especially when assessing shear stress and drag forces.
Detailed Explanation
The assumption of a nearly zero pressure gradient simplifies equations for flow analysis. This means that within the boundary layer, pressure changes very little as the flow moves parallel to the surface. Understanding this helps in mathematically modeling and predicting how fluids behave as they interact with surfaces, such as wings and other aerodynamic structures.
Examples & Analogies
Think about how a flat balloon stays inflated when you blow air into it. The pressure inside the balloon is consistent, even as air moves through. Similarly, in a boundary layer, the pressure is stable, allowing the flow to remain predictable and manageable.
Derivation of Boundary Layer Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
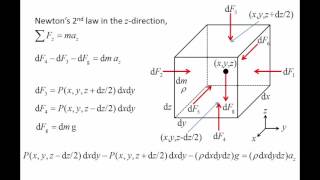
The boundary layer equations are derived using dimensional analysis and simplifications of the Navier-Stokes equations. Key terms involve velocity components, pressure gradients, and viscous forces with assumptions like steady flow and incompressibility.
Detailed Explanation
By simplifying the Navier-Stokes equations, we focus on the dominant forces and remove negligible terms. This allows us to derive the boundary layer equations, which are easier to solve than the complete equations. The derived equations characterize the behavior of forces and velocity changes within the boundary layer, facilitating practical calculations in engineering and fluid dynamics.
Examples & Analogies
Imagine condensing a large book into a short summary. You focus on the most important themes and ideas while leaving out less significant details. Similarly, in fluid dynamics, simplifying complex equations to their essential components makes them easier to understand and apply.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Boundary Layer: A region in fluid flow near a surface where viscous effects significantly influence the flow behavior.
-
Reynolds Number: A dimensionless value indicating the flow regime; critical for distinguishing between laminar and turbulent flows.
-
Flow Separation: A critical phenomenon where fluid departs from the surface of an object, affecting drag and lift.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An airplane wing generates lift due to the airflow creating a boundary layer that affects pressure distribution.
-
In a pipe flow, the boundary layer develops with a parabolic profile where fluid velocity near the wall is slower due to viscous forces.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a boundary near a surface, flow is thin,
📖 Fascinating Stories
-
Imagine a car racing down a road. As it speeds by, the air close to the car's surface whispers softly, turning turbulent behind it, just like a boundary layer!
🧠 Other Memory Gems
-
B.L. for Boundary Layer; remember that fluid layers near surfaces are affected by viscosity!
🎯 Super Acronyms
B.R.T. - Boundary Layer, Reynolds, Transition - key concepts in fluid mechanics!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Boundary Layer
Definition:
A thin layer of fluid in the vicinity of a solid boundary where viscous effects are significant.
-
Term: Reynolds Number
Definition:
A dimensionless quantity used to predict flow patterns in different fluid flow situations, indicating the ratio of inertial forces to viscous forces.
-
Term: Laminar Flow
Definition:
A type of fluid flow in which fluid moves in smooth paths or layers, typically at low Reynolds numbers.
-
Term: Turbulent Flow
Definition:
A type of fluid flow characterized by chaotic changes in pressure and flow velocity, typically at high Reynolds numbers.
-
Term: Flow Separation
Definition:
The phenomenon in which the fluid flow separates from the surface of a body, causing a loss of lift and an increase in drag.