Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Boundary Layers
Unlock Audio Lesson
Good morning, class! Today, we'll start our discussion on boundary layers. Can anyone tell me why understanding boundary layers is essential in fluid mechanics?
I think boundary layers help us understand how fluid behaves near the surface of an object, right?
Exactly, Student_1! Boundary layers allow us to analyze the velocity gradients near surfaces, providing insights into drag forces. These layers greatly impact designs in aerospace and mechanical engineering.
How do the properties of the boundary layer change with different flow conditions?
Excellent question! The Reynolds number helps us classify flow conditions as laminar or turbulent, affecting boundary layer behavior. Remember: as Reynolds numbers increase, boundary layers become thinner. This is crucial in applications like aircraft design.
Is there a specific equation we will derive today for analyzing boundary layers?
Yes, we'll derive the boundary layer equations from the Navier-Stokes equations. Let's keep this in mind: these approximations make it simpler to analyze fluid flow problems!
To summarize, boundary layers are important for assessing how fluids interact with surfaces, particularly in high-speed flow conditions. Let's dive deeper into the equations.
Deriving Boundary Layer Equations
Unlock Audio Lesson
Now, who can remind us of the significance of the Navier-Stokes equations in fluid mechanics?
They describe how fluid motion is affected by viscosity and flow behavior.
Correct! Now, to derive boundary layer equations, we often simplify these equations by making several assumptions, like steady flow and two-dimensionality. Can someone explain what we mean by 'no-slip boundary conditions'?
It means that the fluid in contact with the surface has zero velocity relative to the surface, right?
Exactly! Understanding these conditions is crucial as they influence our derived equations. Next, we will focus on non-dimensionalization. Can anyone tell me why we non-dimensionalize equations?
To simplify the equations and compare different flow characteristics.
Great answer, Student_2! Non-dimensionalization helps us analyze the effects of Reynolds number on flow. Now, let’s explore the boundary layer equations that we can derive.
In summary, we've established that we start from the Navier-Stokes equations, apply boundary conditions, and work our way to the boundary layer equations using simplifications and non-dimensionalization.
Reynolds Number and Flow Characteristics
Unlock Audio Lesson
Let's move on to the concept of Reynolds number! How many of you understand its significance in boundary layer analysis?
It's a ratio that helps us determine whether the flow is laminar or turbulent, isn’t it?
Exactly, Student_3! When Reynolds numbers are low, the flow is laminar and when they reach values above approximately 5 x 10^5, the flow tends toward turbulence.
So, as Reynolds numbers increase, what happens to boundary layer thickness?
Excellent question! Generally, boundary layer thickness decreases as Reynolds numbers increase, leading to thinner layers in high-velocity flows.
And what practical implications does this have for engineering designs?
Knowing boundary layer behavior is critical for minimizing drag and enhancing performance. For instance, in designing aircraft wings, understanding these principles helps reduce fuel consumption.
To wrap up, understanding Reynolds number allows engineers to predict flow behavior around objects, significantly impacting design decisions in various industries.
Numerical Solutions and Applications
Unlock Audio Lesson
As we shift gears to computational techniques, who can tell me why numerical solutions are becoming essential in fluid dynamics?
Because they allow us to solve complex problems that are too difficult for analytical methods.
Exactly! With advancements in computational fluid dynamics, we can effectively analyze boundary layer equations without painstaking analytical solutions.
What type of problems can we solve with CFD?
CFD can help us simulate conditions like airflow over wings, heat transfer, and even weather patterns. It’s an invaluable tool in modern engineering.
How do we ensure accuracy in CFD results?
Great question! Ensuring mesh quality, selecting appropriate models, and validating with experimental data are key to achieving accurate results.
In summary, numerical solutions empower us to tackle complex fluid dynamics issues, offering efficient and accurate results, especially in analyzing boundary layers.
Applying Boundary Layer Equations
Unlock Audio Lesson
Finally, let’s discuss practical applications of boundary layer equations. Who can give an example?
In aerospace engineering, we need to understand how air flows around wings to minimize drag.
Exactly, Student_2! Understanding the boundary layer helps us improve aerodynamic efficiency and performance in aircraft and vehicles.
What about in civil engineering? Are boundary layers relevant there?
Absolutely! Boundary layer concepts apply to structures such as bridges and buildings, where wind load assessments rely on understanding flow characteristics around surfaces.
So, in essence, boundary layers are fundamental in many fields?
Yes! From weather forecasting to vehicle design and energy efficiency, boundary layer principles play a significant role across various disciplines.
To conclude our session, remember that boundary layer equations are crucial for analyzing and solving fluid flow problems, impacting multiple engineering fields.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concept of boundary layers is explored in detail, including the derivation of boundary layer equations from the Navier-Stokes equations, their applications in understanding laminar flow, and the significance of Reynolds numbers in determining flow characteristics.
Detailed
Boundary Layer Equations
The study of boundary layers is vital in fluid mechanics, particularly in simplifying complex fluid flow problems. This section focuses on deriving the boundary layer equations, which are approximations of the fundamental Navier-Stokes equations, specifically suited for analyzing flow around bodies, such as flat plates in laminar flow scenarios. Throughout the lecture, key topics include defining boundary layers, understanding their characteristics, and discussing the Reynolds number's influence on flow behavior.
Key Points:
- Introduction to Boundary Layers: The section begins with a discussion on the concept of boundary layers, emphasizing their importance and utility in fluid mechanics, particularly in relation to Navier-Stokes equations.
- Deriving Boundary Layer Equations: This involves a systematic approach, incorporating approximations and assumptions such as steady flow, two-dimensionality, and neglecting body forces (e.g., gravity).
- Reynolds Number and Flow Characteristics: The relationship between Reynolds number, boundary layer thickness, and flow transition from laminar to turbulent is thoroughly explained, with practical implications for engineering design.
- Numerical Solutions and Applications: Emphasizing modern computational fluid dynamics (CFD) tools, the section highlights how these equations can be solved numerically, making traditional analytical techniques less necessary.
- Boundary Layer Problems: Various practical applications are explored, particularly in aerodynamics, emphasizing how to approach boundary layer problems using the Euler equations in tandem with derived boundary layer equations.
Understanding boundary layer equations is crucial for effectively managing flow behavior in various engineering applications, from aircraft design to hydraulic structures.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Boundary Layers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
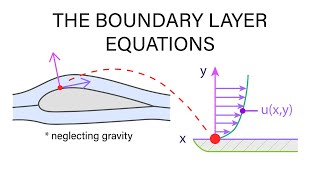
In the last class, we discussed the utility of the boundary layer concept as well as demonstrated different types of boundary layers, such as those that form when flow past an object, mixing layers, wake formations, and jet formations. Boundary layers are essential in understanding fluid behavior and can be solved as part of approximation solutions of the Navier-Stokes equations (basic equations of fluid flow).
Detailed Explanation
This chunk introduces the concept of boundary layers in fluid mechanics. Boundary layers are regions in fluid where the velocity changes from zero (due to the no-slip condition at the boundary) to the free stream velocity. Understanding these layers helps in analyzing flow patterns around objects. The chunk emphasizes how boundary layers can be approximated using simpler equations derived from the more complex Navier-Stokes equations.
Examples & Analogies
Consider a slice of bread in a moving car. As the car moves, the outer layer of air hits the bread, and the air closest to the bread (the boundary layer) moves slower than the air further away from the bread. This slow-moving layer of air around the object is similar to the boundary layer concept in fluid dynamics.
Laminar Flow and Boundary Layer Thickness
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We look at the laminar flow and how we can solve boundary layer equations to determine boundary layer thickness and flow Reynolds numbers, as well as wall shear stress. If Reynolds number x is less than 10 to the power 5, the flow remains laminar, and as the Reynolds number exceeds 3 into 10 to the power 6, the flow becomes turbulent.
Detailed Explanation
This chunk focuses on the relationship between Reynolds numbers and flow types. Reynolds numbers help determine whether the flow will be laminar (smooth) or turbulent (chaotic). A Reynolds number below 100,000 suggests laminar flow, where the boundary layer is predictable and smooth. In contrast, a Reynolds number above 3,000,000 indicates turbulent flow, which introduces complexities such as irregular patterns and increased drag.
Examples & Analogies
Imagine a river flowing over rocks. When the water flows slowly (low Reynolds number), it moves smoothly over the rocks – this is similar to laminar flow. As the water speeds up and hits the rocks harder, it splashes and churns, creating turbulence – similar to turbulent flow with a high Reynolds number.
Basic Concepts of Boundary Layer Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Today, we will discuss the simplifications of the Navier-Stokes equations to derive the boundary layer equations. The first assumption is that we consider steady flow, neglecting any unsteady components and gravity. We will also focus on two-dimensional flows for initial analysis.
Detailed Explanation
In this chunk, we discuss the approach to simplifying the Navier-Stokes equations to understand boundary layers better. By making assumptions about steady-flow and two-dimensional effects, we can derive equations that allow us to explore boundary layer behavior without the complexity introduced by gravity and changes in time. This simplification greatly aids in practical calculations for engineering applications.
Examples & Analogies
Think of riding a bicycle at a steady speed on a flat road. The flow of air around you can be simplified because you are not changing speed (steady flow) or going up and down hills (neglecting gravity). This is akin to simplifying complex equations to make them manageable and easier to understand.
Assumptions for Deriving Boundary Layer Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When deriving boundary layer equations, we assume that gravity forces are negligible since they act on a horizontal plane and do not significantly impact the flow. The analysis focuses on the inertia forces being significantly larger than viscous forces.
Detailed Explanation
Here, the chunk highlights crucial assumptions made during the derivation of boundary layer equations. Ignoring gravity implies that the forces due to fluid motion (inertia) are much stronger than any forces due to weight (gravity). This allows us to focus on how the fluid behaves horizontally around objects, simplifying our calculations and models.
Examples & Analogies
Picture a ball rolling on a flat, smooth surface. The main force at play is the ball's momentum and how it interacts with the surface – gravity is not influencing its motion significantly on a flat surface. In boundary layer analysis, we similarly ignore gravity to focus on the effects of fluid motion.
Order of Magnitude Analysis in Boundary Layers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We determine the order of each term in the Navier-Stokes equations and apply non-dimensionalization to analyze the components. This process helps to identify which terms dominate and which can be neglected in boundary layer conditions.
Detailed Explanation
This chunk explains a technique called order of magnitude analysis, which helps us identify the key physical processes governing flow in the boundary layer. By analyzing the dimensions and scales of various terms, we determine which can be neglected, leading us to simplified equations that describe the flow behavior accurately.
Examples & Analogies
Imagine a busy highway where many cars are traveling. If you want to analyze traffic conditions, you can focus on the cars moving fast (main traffic flow) and ignore the occasional bicycle on the side of the road (negligible effects). In boundary layer flow, we identify the dominant forces and neglect those with little influence.
Application of Bernoulli's Principle in Boundary Layer Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To derive the boundary layer equations more effectively, we apply Bernoulli's principle along the streamline, stating that pressure along the streamline remains constant if there are no external work or energy sources, allowing relationships to be formulated more straightforwardly.
Detailed Explanation
Applying Bernoulli's principle in boundary layer analysis simplifies the process further. It tells us that for streamlined flow, pressure remains relatively constant, enabling us to correlate velocity and pressure dynamics easily. Using this principle allows for a more straightforward derivation of the boundary layer equations while maintaining accuracy.
Examples & Analogies
Consider how a garden hose works. When you put your finger partway over the end of the hose, the water speeds up and shoots out further, but the pressure at the hose's main body remains unchanged. This principle embodies how Bernoulli's principle assists in analyzing flow in boundary layers.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Boundary Layer: The region where viscosity affects fluid movement near surfaces.
-
Navier-Stokes Equations: The governing equations for fluid motion, essential in deriving boundary layer equations.
-
Reynolds Number: A crucial parameter for determining flow regimes and related phenomena.
-
No-Slip Condition: The principle that fluid velocity is zero at solid surfaces, impacting boundary layer thickness.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The flow of air over an airplane wing, where the boundary layer affects lift and drag.
-
Simulation of flow around a flat plate in wind tunnel tests for determining the boundary layer thickness.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a layer thin and small, viscous forces rule it all. Boundary layer's what we see, where flow's affected near to me.
📖 Fascinating Stories
-
Imagine a little fish swimming close to the bank of a river; it experiences different water flow than a fish in the middle of the stream. This story reminds us of how boundary layers work—where viscosity creates variations in flow near surfaces.
🧠 Other Memory Gems
-
Remember 'B.R.A.' for Boundary Layer concepts: 'B' for Boundary layer, 'R' for Reynolds number, and 'A' for Aerodynamics.
🎯 Super Acronyms
Boundary Effects Impacting Flow = BEIF (Boundary Layer, Effects of Viscosity, Impact of Streamlines).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Boundary Layer
Definition:
A thin region adjacent to a solid surface where the effects of viscosity influence the flow characteristics.
-
Term: NavierStokes Equations
Definition:
Fundamental equations governing fluid motion which describe how velocity, pressure, density, and viscosity affect fluid dynamics.
-
Term: Reynolds Number
Definition:
A dimensionless quantity that helps predict flow patterns in different fluid flow situations by comparing inertial forces to viscous forces.
-
Term: Flow Transition
Definition:
The process whereby flow changes from laminar to turbulent, often influenced by the Reynolds number.
-
Term: NoSlip Condition
Definition:
A boundary condition in fluid mechanics stating that the fluid velocity at the surface of a solid boundary is zero.
-
Term: Computational Fluid Dynamics (CFD)
Definition:
A branch of fluid mechanics that uses numerical methods and algorithms to analyze and solve problems involving fluid flows.