Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Non-dimensionalization
Unlock Audio Lesson
Today, we’ll discuss non-dimensionalization, a powerful tool in fluid mechanics. Who can explain what it means to non-dimensionalize a variable?
It means to convert it into a dimensionless form by removing its units.
Exactly! Non-dimensionalization helps us compare different systems. For example, we often use Reynolds numbers in fluid dynamics. Can anyone remind me what Reynolds number signifies?
It relates inertial forces to viscous forces in a fluid.
So, higher Reynolds numbers indicate more turbulent flow, right?
Correct! So, as we transform our variables, we can analyze their behaviors across different conditions without needing to solve each scenario individually.
*Summary*: Non-dimensionalization simplifies complex equations by stripping away units and using dimensionless numbers to generalize fluid behavior across various conditions.
Order of Magnitude Analysis
Unlock Audio Lesson
Next, we’ll explore order of magnitude analysis. Why do we use it in fluid dynamics?
To estimate which forces or terms in an equation dominate and which can be ignored!
Exactly! This allows us to simplify our equations. Can someone give an example of how we use this in boundary layers?
We analyze the terms in the Navier-Stokes equations to decide which factors are significant when calculating flow behavior.
Right! This is especially important when considering laminar versus turbulent flows in boundary layers. Remember, for laminar flow, the Reynolds number stays below 10^5.
*Summary*: Order of magnitude analysis helps identify dominant terms in fluid equations, easing the transition to simplified models, particularly when analyzing boundary layers.
Application in Boundary Layers
Unlock Audio Lesson
Now, let's apply what we've learned to boundary layer theory. Why is it critical to consider both non-dimensionalization and order of magnitude analysis here?
Because in boundary layers, flow behavior changes significantly compared to free-stream conditions, and these techniques simplify our analysis!
Absolutely! By approximating values and identifying which pressure gradients are negligible, we can derive applicable boundary layer equations.
So, we can identify when laminar flow transitions into turbulence based on our Reynolds number calculations.
*Summary*: In boundary layers, the integration of non-dimensionalization and order of magnitude analysis is crucial for simplifying Navier-Stokes equations and understanding flow transitions.
Challenges in Boundary Layer Analysis
Unlock Audio Lesson
Finally, let’s discuss challenges in boundary layer analysis. What are some obstacles we may encounter?
Dealing with turbulence makes it difficult to establish accurate models!
Exactly! Turbulent flows introduce complexities that our current techniques might not capture adequately. Can anyone think of how we might address these challenges?
We could use computational fluid dynamics simulations, as they can handle complex behaviors.
*Summary*: Challenges in boundary layer analysis include turbulence and modeling difficulties, with computational techniques like CFD providing ways to overcome these issues.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the concepts of non-dimensionalization and order of magnitude analysis as critical tools for simplifying fluid mechanics problems. Emphasizing boundary layer theory, we outline the significance of these techniques in practical and theoretical applications, especially concerning laminar and turbulent flow behavior.
Detailed
Non-dimensionalization and Order of Magnitude Analysis
This section focuses on two essential techniques in fluid mechanics: non-dimensionalization and order of magnitude analysis. Both methods are relevant in simplifying complex equations such as the Navier-Stokes equations, particularly when analyzing fluid behavior in boundary layers.
Key Concepts
- Non-dimensionalization involves transforming physical quantities into dimensionless numbers to simplify mathematical relationships. This aids in generalizing solutions across various scenarios.
- Order of magnitude analysis provides a qualitative understanding of the relative importance of various terms in equations, allowing us to identify dominant effects and potentially negligible components.
In boundary layer analysis, we look closely at laminar flow over flat plates. When the Reynolds number is below a critical threshold (around 10^5), the flow remains laminar. As the Reynolds number increases beyond this value, the flow transitions to turbulence.
The integration of these methods enables engineers and scientists to approximate solutions to fluid flow problems more easily and opens pathways for computational fluid dynamics (CFD) techniques. By clarifying the assumptions underlying these analyses, we can establish effective boundary layer equations and elucidate their practical applications in engineering contexts.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Non-dimensionalization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The basic equations if it is a steady okay so that means we do not have a local accelerations components. So you will have the component of rho as we bacterial forms is equal to minus great P if you remove the gravity components gravity is neglected okay.
Detailed Explanation
In fluid mechanics, non-dimensionalization is the process of converting physical quantities into dimensionless numbers. This is essential because it helps to simplify the equations governing fluid flow, allowing for easier analysis. In this context, neglecting gravity and local acceleration simplifies the basic governing equations, focusing solely on the relationship between different forces acting on the fluid.
Examples & Analogies
Think of a recipe that requires specific measurements. If you were to scale up the recipe, you could convert all measurements to a common size, making it easier to adjust without worrying about the individual units (like teaspoons vs. cups). Similarly, non-dimensionalization helps convert different physical quantities into a standard format that makes analysis more straightforward.
Order of Magnitude Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We always try to look it if I expand these terms okay if I expand these terms okay which as I did it earlier it will have a big expressions. From that which are the terms having what is the order? That means if I normalize okay, we look it to normalize the components okay, if you non-dimensionalized okay.
Detailed Explanation
Order of magnitude analysis involves estimating the relative sizes or orders of different terms in an equation. This technique helps identify which terms can be neglected without significantly affecting the outcome of a calculation. In the context of fluid dynamics, we can identify dominant forces and simplify equations by focusing on the most significant terms, often leading to simpler forms of the Navier-Stokes equations.
Examples & Analogies
Imagine you want to estimate how long it will take you to travel to a nearby city. You might focus on the driving time, ignoring small factors like stopping at traffic lights. This approach allows you to predict your travel time without getting bogged down in less significant details. Similarly, in fluid mechanics, identifying which forces to consider helps streamline complex equations.
Non-dimensional Equations Derivation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look at the same concept of non-dimensionalization and look at how we can derive bounded layer equations that is what is our idea.
Detailed Explanation
The derivation of non-dimensional boundary layer equations begins with the fundamental principles of fluid flow. By normalizing the variables such as velocity and pressure using characteristic scales, we obtain dimensionless equations. These equations maintain the fundamental relationships while allowing us to explore the flow behavior under varying conditions without dealing with individual units.
Examples & Analogies
Consider a scale model of a bridge designed using specific units versus creating a ratio representation. The latter allows engineers to discuss the design without getting caught up in the actual measurements, making it easier to communicate ideas and make adjustments based on the modeled behaviors.
Implications of Reynolds Number
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at each terms that as we do the boundary layer thickness we were talking about we are talking about very higher Reynolds numbers okay is close to the 1 is to 10 to the power 5.
Detailed Explanation
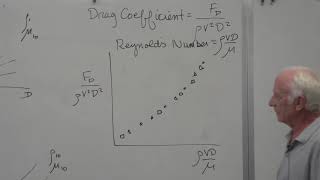
Reynolds number is a dimensionless value that characterizes flow regimes, indicating whether the flow is laminar or turbulent. A Reynolds number below 10^5 suggests laminar flow, while values above indicate turbulence. In boundary layer theory, understanding the Reynolds number is crucial because it impacts the thickness of the boundary layer and helps predict flow behavior around objects.
Examples & Analogies
Think of Reynolds number like an indicator of traffic conditions. Low values resemble calm roads with steady traffic (laminar flow), while high values represent heavy, chaotic traffic (turbulent flow). Just as traffic flow changes dynamics, the behavior of fluid around surfaces also evolves with the Reynolds number.
Simplification of Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So that means we can neglect these two terms. But what we can do it we can inspect these two that since there is a multiplications with L by the delta which is boundary layer thickness.
Detailed Explanation
In boundary layer analysis, certain terms in the Navier-Stokes equations can be neglected based on their relative magnitudes. This leads to simpler forms of the equations that retain essential characteristics of fluid behavior. By conducting a thorough order of magnitude analysis, we can identify non-dominant terms, enabling more straightforward solutions without losing important dynamics.
Examples & Analogies
Imagine simplifying a blueprint by removing small details that won't affect the overall design. This simplification makes it easier to visualize the structure as a whole while ensuring the primary features remain intact. Similarly, neglecting lesser terms in complex equations retains essential fluid characteristics while making the analysis more manageable.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Non-dimensionalization involves transforming physical quantities into dimensionless numbers to simplify mathematical relationships. This aids in generalizing solutions across various scenarios.
-
Order of magnitude analysis provides a qualitative understanding of the relative importance of various terms in equations, allowing us to identify dominant effects and potentially negligible components.
-
In boundary layer analysis, we look closely at laminar flow over flat plates. When the Reynolds number is below a critical threshold (around 10^5), the flow remains laminar. As the Reynolds number increases beyond this value, the flow transitions to turbulence.
-
The integration of these methods enables engineers and scientists to approximate solutions to fluid flow problems more easily and opens pathways for computational fluid dynamics (CFD) techniques. By clarifying the assumptions underlying these analyses, we can establish effective boundary layer equations and elucidate their practical applications in engineering contexts.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The relationship between the Reynolds number and flow behavior, where values below 10^5 indicate laminar flow.
-
Application of Bernoulli's equation along streamlines to deduce pressure variations in fluid flow.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid's dance, force and flow, non-dimensional numbers make it glow.
📖 Fascinating Stories
-
Imagine a small stream under a bridge where the flow is so smooth and organized — it's a laminar flow. The bridge doesn't jam it up, just lets it flow at peace. Now, picture a storm stirring wild waves — that chaotic mixture is turbulent!
🧠 Other Memory Gems
-
N for Non-dimensionalization, O for Order of magnitude, R for Reynolds number, B for Boundary layer!
🎯 Super Acronyms
NRO - Non-dimensionalization, Reynolds, Order (of Magnitude)!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Nondimensionalization
Definition:
The process of converting physical quantities into dimensionless numbers to simplify equations and allow for generalization across problems.
-
Term: Order of Magnitude Analysis
Definition:
A technique used to estimate the relative significance of different terms in an equation by comparing their magnitudes.
-
Term: Reynolds Number
Definition:
A dimensionless number that signifies the ratio of inertial forces to viscous forces in fluid flow, influencing the transition between laminar and turbulent flow.
-
Term: Boundary Layer
Definition:
A thin region adjacent to a solid boundary where fluid velocity changes from zero at the surface to the free stream value.
-
Term: NavierStokes Equations
Definition:
A set of nonlinear partial differential equations describing the motion of fluid substances.
-
Term: Laminar Flow
Definition:
A type of fluid flow characterized by smooth, orderly motion, typically occurring at low Reynolds numbers.
-
Term: Turbulent Flow
Definition:
A type of fluid flow that is chaotic and irregular, typically occurring at high Reynolds numbers.