Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Reynolds Numbers
Unlock Audio Lesson
Let's start with the Reynolds number. It's a crucial concept in fluid mechanics, representing the ratio of inertial forces to viscous forces. Can anyone tell me why this ratio is important?
It helps in determining whether the flow is laminar or turbulent!
Exactly! When we look at fluid flow around objects, a low Reynolds number indicates a laminar flow, while a high Reynolds number indicates a more chaotic turbulent flow. We can remember it using the mnemonic: 'LAMinarglow and TurbulentThrow.'
So, what is the critical Reynolds number to look out for?
Great question! The critical Reynolds number for flow transitioning from laminar to turbulent is around 1×10^5. Just below this threshold, we have laminar flow—smooth and orderly.
Flow Characteristics
Unlock Audio Lesson
Let’s delve deeper into the characteristics of laminar versus turbulent flows. Can anyone describe how they differ?
Laminar flow is smooth, while turbulent flow is chaotic and has eddies or vortices.
That's right! Laminar flow shows a linear velocity profile where fluid layers slide past each other, whereas turbulent flow has a more irregular profile with fluctuations. Think of how a calm river differs from a raging storm!
But how does this relate to Reynolds numbers?
The Reynolds number helps quantify the flow characteristics. When we conduct experiments and find the flow transitions around that critical Reynolds number, we can expect a shift in these behaviors.
Boundary Layer Theory
Unlock Audio Lesson
Now, can anyone tell me about boundary layers? Why are they significant in our discussions about flow characteristics?
Boundary layers represent the region of fluid near a surface where effects of viscosity are significant.
Correct! The boundary layer thickness is critical for determining drag forces on objects. We have large inertial forces acting in the flowing part of the fluid, but within the boundary layer, viscous forces play a dominant role.
What happens if the boundary layer becomes turbulent?
If the boundary layer transitions to turbulent flow, this can significantly increase skin friction drag but may also enhance mixing, depending on the application. Understanding when and how this transition occurs is crucial for engineers.
Applications of Reynolds Numbers
Unlock Audio Lesson
Let’s wrap up by discussing the practical implications of Reynolds numbers in engineering. How can this knowledge be applied in real-life scenarios?
It’s important in designing vehicles and aircraft where fluid dynamics play a crucial role.
Absolutely! Designers must consider how the transition between laminar and turbulent flow occurs to reduce drag and enhance performance. Let's remember this with the acronym: 'FLOW'—Friction, Lift, Optimal performance, and Wakes!
Also, in contexts like pipeline flow and HVAC systems, the Reynolds number helps predict flow behavior.
Spot on! All these factors combine to give engineers insights that help in optimizing designs.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on critical Reynolds numbers and their implications in fluid mechanics, detailing how flow transitions occur from laminar to turbulent states and the role of boundary layer approximations in solving fluid dynamics problems.
Detailed
Critical Reynolds Numbers and Flow Characteristics
This section focuses on the critical Reynolds numbers that demarcate different flow characteristics within fluids. A Reynolds number is a dimensionless quantity used in fluid mechanics to predict flow patterns in different fluid flow situations. It is defined as the ratio of inertial forces to viscous forces and provides insight into whether a flow will remain laminar, transition to a turbulent state, or behave in a certain manner under specific conditions.
The text elaborates on the definitions and properties of laminar and turbulent flows. Specifically, it states that when the Reynolds number is less than 100,000 ( 3 A0x A0= A01, A0= A0Re_{cr}), the flow is predominantly laminar. Above 3 million ( A03 A0x A0= A01, A0= A0Re{t}), turbulence begins, creating complex flow dynamics characterized by random fluctuations and vortices.
Understanding critical Reynolds numbers is essential for engineers and scientists in the design and analysis of systems, particularly in aerospace and civil engineering applications where fluid behavior significantly influences performance and efficiency. This section also touches upon boundary layer concepts, addressing how transitions between flow states impact flow characteristics, such as the thickness of boundary layers and resulting shear stresses.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Flow Regimes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If Reynolds number x is less than 10^5 (1 lakh), the flow remains laminar. There will be transitions, leading to fully turbulent behavior when Reynolds numbers exceed 3 x 10^6 (3 million).
Detailed Explanation
This chunk introduces the concept of Reynolds number, a dimensionless quantity that helps to predict flow patterns in different fluid flow situations. When the Reynolds number is below 100,000, the flow tends to be smooth and orderly, known as laminar flow, where fluid layers slide past one another without mixing. As the Reynolds number increases and surpasses this threshold, the flow starts to transition to turbulence, a chaotic flow regime where fluid particles intermingle, creating vortices and irregularities.
Examples & Analogies
Imagine watching a calm river water flow. When the water is moving slowly (like laminar flow), you can see how layers of water glide past each other smoothly. However, when the water speeds up significantly, it begins to bubble, churn, and mix (like turbulent flow), making it impossible to distinguish distinct layers.
Boundary Layer Thickness
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The thickness of the boundary layer is defined where the velocity is approximately 99% of the free stream velocity. For engineering applications, we focus on places where the velocity approaches this threshold.
Detailed Explanation
In fluid dynamics, the boundary layer is the thin region close to a surface (like a flat plate) where viscous forces are significant. The boundary layer thickness δ is defined as the distance from the surface to a point where the fluid velocity reaches 99% of the free stream velocity (v). This concept is crucial in various engineering applications because it determines how much drag force will act on an object moving through a fluid. Engineers need to understand and predict this boundary layer to design more efficient structures, such as wings of airplanes and hulls of ships.
Examples & Analogies
Think about sliding a piece of paper across a table. Initially, the paper experiences some friction due to the slow motion of the air in contact with its surface. As you slide faster, the air has less time to 'stick' to the paper, and thus the effect of the air begins to lessen. The boundary layer concept is similar; it helps understand how much air (or any fluid) is affected by an object moving through it.
Avoiding Transitional Zones
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In engineering, we aim to avoid transitional zones that lead to turbulence, as they often result in increased drag and additional noise. Techniques like tripwires can be used to manage these zones.
Detailed Explanation
Transitional zones are areas where the flow changes from laminar to turbulent. These zones can cause inefficiencies in designs because turbulent flow creates more drag, which can hinder performance and increase energy costs. Engineers often implement strategies, such as the introduction of tripwires or other surface modifications, to ensure that the flow remains laminar as long as possible, reducing turbulence, drag, and noise.
Examples & Analogies
Think of a calm wind blowing through trees. The leaves flutter gently. However, if a gust of wind suddenly sweeps through, it causes chaotic movement and noise. Similarly, by placing a small obstacle (like a tripwire) in a water flow, we can keep the flow orderly far longer, preventing the onset of turbulence.
Experimental Verification of Flow Characteristics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
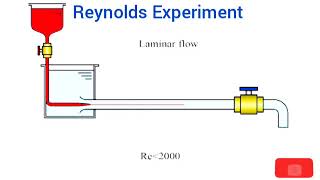
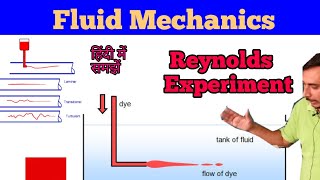
Experiments, such as those conducted in wind tunnels, have established critical Reynolds numbers for identifying laminar and turbulent flow behaviors.
Detailed Explanation
To determine the characteristics of fluid flow around various shapes, extensive experiments have been conducted, notably in controlled environments like wind tunnels. These experiments help in confirming the theoretical predictions about where the flow becomes laminar or turbulent by observing the behavior of fluid particles at different velocities and Reynolds numbers. This empirical data is essential for validating mathematical models and ensuring they align with real-world outcomes.
Examples & Analogies
Consider how scientists might test different designs of airplane wings in a wind tunnel to see how air flows over them. By adjusting the speed of the air and measuring the resulting drag and flow patterns, they can confirm when the airflow is smooth or starts to turbulent, just as engineers need to know to ensure efficient designs.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Reynolds Number: A key dimensionless number that indicates the flow regime of a fluid.
-
Laminar Flow: Characterized by orderly and smooth fluid motion.
-
Turbulent Flow: Chaotic flow regime with eddies and vortices.
-
Boundary Layer: The layer next to a surface where viscous effects are significant.
-
Critical Reynolds Number: The threshold separating laminar and turbulent flows.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of laminar flow: Oil flowing slowly through a pipe at low velocities.
-
Example of turbulent flow: Water rushing through a narrow river, creating eddies.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Flow so slow, all in a line, under 100K, smooth and fine. Over that mark, things get wild, eddies and swirls, the flow goes wild.
📖 Fascinating Stories
-
Imagine a race between a sleek fish (laminar flow) and a chaotic octopus (turbulent flow). The fish glides effortlessly while the octopus creates splashes and whirlpools, illustrating the difference between laminar and turbulent flows.
🧠 Other Memory Gems
-
For Reynolds Number, think 'Low is Laminar, High is Turbulent' — LHT.
🎯 Super Acronyms
FLOW
- Friction
- Lift
- Optimal performance
- Wakes.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Reynolds Number
Definition:
A dimensionless quantity representing the ratio of inertial forces to viscous forces in fluid flow.
-
Term: Laminar Flow
Definition:
A smooth and orderly type of fluid flow characterized by layers of fluid sliding past one another.
-
Term: Turbulent Flow
Definition:
An irregular and chaotic type of fluid flow with swirling currents and vortices.
-
Term: Boundary Layer
Definition:
The layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity are significant.
-
Term: Critical Reynolds Number
Definition:
The Reynolds number threshold at which flow transitions from laminar to turbulent.
-
Term: Skin Friction Drag
Definition:
The drag force experienced by an object due to the friction between the object and the fluid.