Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Reynolds Number and Flow Types
Unlock Audio Lesson
Good morning, everyone! Today, let's begin by discussing the Reynolds number. Can someone tell me what it represents in fluid dynamics?
Isn't it the ratio of inertial forces to viscous forces in a fluid?
Exactly! Remember, we can use the acronym 'IV' to help us remember: 'I' for Inertial and 'V' for Viscous. Now, as the flow rate increases, what happens to the flow type?
It changes from laminar to turbulent?
Correct! The threshold for this change is around a Reynolds number of 100,000. So, what do we refer to this intermediate state?
Transitional flow?
Exactly again! Great job, everyone! Transitioning between these states is vital for understanding how we design systems in civil engineering.
Characteristics of Laminar and Turbulent Flow
Unlock Audio Lesson
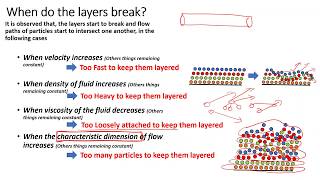
Moving on, can anyone explain how laminar flow differs from turbulent flow in terms of behavior and velocity profiles?
Laminar flow is smooth and layers of fluid slide past each other, while turbulent flow is chaotic with eddies and vortices.
Excellent observation! To remember this, consider the mnemonic 'Smooth Layers vs. Chaotic Currents'. Timely, could you elaborate on the implications of these flow types?
Of course! Laminar flow has a lower drag than turbulent flow, which affects efficiency, especially in design applications like aircraft.
Spot on! The understanding of these characteristics is essential in various engineering applications.
Boundary Layer Thickness and Transition
Unlock Audio Lesson
Now, let's address boundary layer thickness. What happens to the thickness as we move from laminar to turbulent flow?
It decreases as the Reynolds number increases?
Yes! You can use the mnemonic 'TB = Tension Builds' to recall that thinner boundary layers are associated with higher velocities. Can anyone explain why we want to minimize turbulent effects?
Because turbulent flow has higher drag forces, which can lead to efficiency losses in structures?
Perfect! Now, understanding these transitions will aid in our computational analyses moving forward.
Utilizing CFD Tools
Unlock Audio Lesson
Lastly, let's touch on CFD tools. How has the advent of these tools changed our approach to studying fluid behavior?
CFD allows us to simulate complex flows without the need for extensive physical experiments.
Right! Remember, 'Simulation over Summation' to help recall this change. How about practical applications of these simulations?
We can maximize design efficiency in structures like bridges or aircraft by accurately predicting flow transitions!
Exactly! That's the heart of applying fluid mechanics to engineering!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the transition from laminar to turbulent flow in fluid mechanics, emphasizing the role of Reynolds numbers and boundary layer characteristics. It explains the flow dynamics in relation to various fluid scenarios, highlighting the importance of calculations in predicting flow behavior around objects.
Detailed
Laminar to Turbulent Transition
This section delves into the transition from laminar to turbulent flow, a critical concept in fluid mechanics. The transition is heavily influenced by the Reynolds number, a dimensionless quantity representing the ratio of inertial forces to viscous forces in a fluid.
- Laminar Flow: Flow remains laminar when the Reynolds number (Re) is less than 100,000, characterized by smooth and orderly fluid motion.
- Transitional Flow: As Re approaches 100,000, the flow characteristics start to transition, indicating the onset of small vortices while retaining some laminar traits.
- Turbulent Flow: When Re exceeds 3,000,000, the fluid shows fully turbulent behavior, resulting in chaotic and irregular fluid motion which significantly impacts drag forces.
The section illustrates practical implications, including wall shear stress and boundary layer thickness, while discussing methods like computational fluid dynamics (CFD) to analyze these transitions thoroughly.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Laminar and Turbulent Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
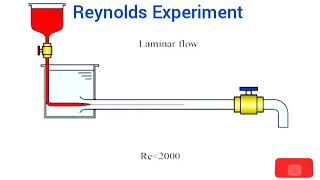
If Reynolds numbers in terms of characteristic length X is less than 10^5 (1 lakh), the flow remains laminar. When Reynolds numbers exceed 3 x 10^6 (3 million), the flow becomes turbulent.
Detailed Explanation
Reynolds number is a crucial parameter in fluid mechanics that helps characterize the flow regime of a fluid. If the flow has a Reynolds number below 100,000, it indicates laminar flow where fluid particles move in parallel layers without mixing. As the Reynolds number increases and surpasses 3,000,000, the flow transitions into turbulence, where chaotic changes in pressure and flow velocity occur. This transition can be visualized through experiments and is fundamental to designing systems like aircraft and pipelines where controlling flow is vital.
Examples & Analogies
Think of a calm river versus a fast-flowing stream. In the calm river (laminar flow), the water flows smoothly without disturbances. If you observe the fast stream or the river during a storm (turbulent flow), you will notice churning water with many swirls and vortexes. This change resembles how Reynolds number influences the smoothness or chaos of fluid movement.
Boundary Layer Thickness Variation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The thickness of the boundary layer representing where the flow velocity is close to 99% of the free stream velocity decreases with increasing Reynolds numbers.
Detailed Explanation
The boundary layer is a thin region near the surface of an object where the effects of viscosity are significant. As the Reynolds number increases, inertia becomes dominant over viscosity, leading to a thinner boundary layer. Engineers use this concept to predict how fluid flows over surfaces in applications like airplane wings, where understanding the thickness of this layer can impact drag and lift forces.
Examples & Analogies
Imagine a child sliding down a slide. When they start at the top (low Reynolds number), they slide down smoothly. As they gain speed (higher Reynolds number), they might experience less friction from the surface, indicating how a boundary layer gets thinner as speed increases. This metaphor helps understand how objects in fluids react differently at varying speeds.
The Importance of Transition Zones
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Transitional zones are responsible for acoustic noise and other disturbances, so engineers often introduce tripwires to decrease these zones and maintain laminar flow.
Detailed Explanation
Transitional zones are areas where the flow begins to change from laminar to turbulent. These zones can generate noise and increase drag, which can be unfavorable in many engineering applications. By introducing tripwires or other disturbances on surfaces, engineers can manipulate the boundary layer's behavior, potentially delaying the transition to turbulence. This strategy not only improves performance but also reduces noise pollution in sensitive environments.
Examples & Analogies
Consider a biker trying to reduce wind resistance. By using a small flag (like a tripwire) on their back, they can influence how the air flows around them, keeping it smooth and reducing drag. This is analogous to how tripwires manage flow transitions in engineering designs.
The Role of Computational Tools
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Modern computational fluid dynamics (CFD) now allow for precise solutions to boundary layer problems without heavy reliance on approximations.
Detailed Explanation
Historically, solving fluid dynamics problems required complex mathematical formulations and approximations. With the advent of computational fluid dynamics, engineers can simulate fluid flow scenarios virtually, leading to accurate predictions of boundary layer behavior without needing to rely solely on theoretical approximations. This has revolutionized how engineers approach fluid mechanics, allowing for quicker iterations and validations of designs.
Examples & Analogies
Imagine an architect using virtual reality to see how a building interacts with wind. Instead of constructing physical models for wind tests, they can adjust and view changes rapidly in a simulation. This process mirrors how CFD helps engineers analyze and optimize designs more efficiently without cumbersome physical trials.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Reynolds Number: Key to determining flow behavior.
-
Laminar Flow: Characterized by orderly fluid motion.
-
Turbulent Flow: Features chaotic fluid behavior.
-
Transitional Flow: The shift between laminar and turbulent states.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Aircraft wings design relies on understanding the transition of airflow to minimize drag.
-
Example 2: Wind tunnel experiments help visualize laminar and turbulent flow properties and transitions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Reynolds number is the name of the game, laminar and turbulent flow aren't the same.
📖 Fascinating Stories
-
Imagine you're a stream of water; first flowing steadily, but suddenly you hit rocks, creating turbulence in the flow. This transition is your Reynolds number at play!
🧠 Other Memory Gems
-
Remember 'LTT' – Laminar is Thin, Turbulent is Thick for flow thickness comparison.
🎯 Super Acronyms
Use 'T.L.C.' for remembering the flow types
- Transitional
- Laminar
- Chaotic (Turbulent).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Reynolds Number
Definition:
A dimensionless number used to predict flow regimes in fluid dynamics, representing the ratio of inertial to viscous forces.
-
Term: Laminar Flow
Definition:
A type of flow characterized by smooth, orderly fluid motion, often occurring at low Reynolds numbers.
-
Term: Turbulent Flow
Definition:
A chaotic flow regime marked by eddies and vortices, typically seen at high Reynolds numbers.
-
Term: Transitional Flow
Definition:
The intermediate flow state between laminar and turbulent flow, occurring at moderate Reynolds numbers.
-
Term: Boundary Layer Thickness
Definition:
The distance from a boundary inside which the velocity of a fluid is significantly affected by the boundary.