Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stream Functions
Unlock Audio Lesson
Good morning! Today, we'll explore the concept of stream functions. Stream functions help us visualize fluid flow through the representation of streamlines. Can anyone tell me what a streamline represents?
I think streamlines show the paths that fluid particles follow in a flow field.
Exactly! Streamlines indicate how fluid moves. Now, when we introduce compressible stream functions, we simplify our analysis of the flows. Remember, stream functions can reduce complex two-dimensional problems into simpler forms. Let’s think of it as a bridge simplifying our calculations.
Why do we need to simplify the equations?
Great question! Simplifying equations allows us to use just one variable to represent velocity, making our calculations much easier and more efficient!
What kinds of flows can we study with these stream functions?
We can apply this concept to various flows, including incompressible flows, compressible flows, and even flows around structures like buildings and airplanes. Let's summarize: stream functions streamline our calculations and help us analyze different fluid flow scenarios effectively.
Applications of Stream Functions in CFD
Unlock Audio Lesson
Building on our last discussion, let's see how stream functions apply in Computational Fluid Dynamics, or CFD. For example, in simulating the airflow around an F-16, can anyone imagine how this helps?
It probably shows how air flows around the jet, right?
Exactly! CFD software visualizes these patterns, displaying streamlines and velocity magnitudes. This helps engineers understand turbulence and flow behavior. Can you think of any other applications?
Maybe in rotating objects, like cylinders?
Yes! In our discussions, we also talked about how we can visualize flows around rotating cylinders by injecting air bubbles. This shows us the unsteady streamlines clearly. Remember, both static and dynamic scenarios can be represented effectively using stream functions.
So stream functions can help us visualize both steady and unsteady flows?
Exactly! To wrap up, stream functions are powerful tools for visualizing complex flow patterns in practical applications like CFD.
Mathematical Foundations of Compressible Stream Functions
Unlock Audio Lesson
Now, let’s delve into the mathematical foundations of compressible stream functions. Who can explain what makes these functions valuable mathematically?
Are we focusing on how the equations get simplified with one dependent variable?
Precisely! By redefining our variables, we can express the flow using just one function. This allows us to solve mass conservation equations more easily.
Does this mean we can ignore some variables to understand the flow better?
Not ignore, but rather transform the equations to make them less complex. With compressible and incompressible flows, we can apply different stream function formulations to achieve this. Remember to differentiate between these methods!
So it's crucial to understand both types when solving problems?
Absolutely! Each type has its unique properties, and understanding them enables us to apply the appropriate equations effectively. Let’s summarize: mathematical formulation simplifies fluid flow analysis by limiting our variables.
Practical Examples and Numerical Problems
Unlock Audio Lesson
Let’s tackle some practical examples to reinforce our understanding of compressible stream functions. Who can present the first problem?
I have an example involving a stream function that needs to verify continuity equations.
Great! What do you think the first step is?
We should calculate the velocity components using the given stream function.
Then we could check if the divergence of velocity is zero, right?
Exactly! By ensuring that the divergence is zero, we can confirm that mass conservation holds true for that flow. Well done, everyone, understanding practical examples is essential to ensure the concepts are accurately applied.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Compressible stream functions simplify the analysis of fluid flows by reducing the complexity of equations involved. This section highlights their application in various flow scenarios, including F-16 simulations and rotating cylinders, as well as the theoretical foundations and mathematical formulations behind their use.
Detailed
Detailed Summary
In fluid mechanics, stream functions are essential tools for analyzing fluid flow, especially in two-dimensional systems. Compressible stream functions not only consider incompressible flows but also address the nuances of compressible flows. The section elaborates on the application of stream functions through simulations of complex scenarios, such as the flight patterns of an F-16 fighter jet and the behavior of fluid around rotating cylinders. By using Computational Fluid Dynamics (CFD), these intricate fluid behaviors can be visualized, offering insights into velocity distributions and pressure gradients. The mathematical formulation of compressible stream functions allows for the conversion of two independent variables, velocity components u and v, into a single dependent variable, thereby facilitating the application of mass conservation equations. This simplification underscores the importance of understanding both theoretical principles and practical applications in fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look at the streamlines, as you know it, let I take a very simple examples. There is a hump or you can say it is a buildings okay, there is a big buildings are there and you have a uniform stream flow, uniform stream flow. So if want to draw a streamlines will go like this, go like this, go like this. So these are the streamlines we can artistically draw.
Detailed Explanation
This chunk introduces the concept of streamlines which represent the path that fluid particles follow in a flow field. In this example, the flow situation around buildings is described, with the assumption of uniform stream flow. The streamlines visually depict how a fluid behaves as it moves past an obstacle (the buildings).
Examples & Analogies
Imagine water flowing around a rock in a river. The way the water curves around the rock is similar to how the streamlines curve around the buildings in the example. The paths of the water particles are like the streamlines.
Concept of Mass Conservation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So I can have a basic mass conservation equations and Bernoulli's equations to solve the problems. That is why the Bernoulli’s equations is very famous because the regions where you have a very very less frictional force components.
Detailed Explanation
This chunk discusses the importance of mass conservation equations and Bernoulli's principle in fluid flow analysis. These equations help us understand how velocity and pressure change in regions with negligible friction, which is critical for predicting fluid behavior in various engineering applications.
Examples & Analogies
Think of a garden hose. When you cover the end with your finger (creating less friction and increasing velocity), the water shoots out faster from the hose than when it's fully open. This is similar to how Bernoulli's equation describes fluid behavior in regions with low friction.
Application of Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
How we can solve these equations? Because there are two independent variable x and y, two dependent variables u and v okay and we can apply this Bernoulli's equations that is not a big issue.
Detailed Explanation
In this chunk, the discussion focuses on how to use stream functions to simplify the analysis of fluid flow. By converting the problem from two dependent variables (u and v) to a single stream function, it becomes easier to satisfy the continuity equations in a two-dimensional flow field.
Examples & Analogies
Imagine trying to track two balloons in the air. If you only focus on their overall path (stream function) rather than the individual movements (u and v), it makes your job simpler. Similarly, stream functions help simplify complex relationships in fluid dynamics.
Defining Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
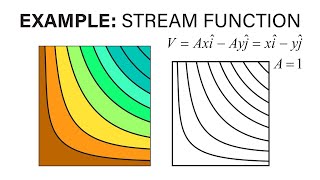
So we are defining a stream functions which is a function of x and y. The stream functions like for example as I said it in case of flow around a building structures.
Detailed Explanation
This chunk elaborates on what stream functions are — specifically, they are mathematical representations that relate to the flow patterns in two-dimensional spaces. By defining the stream function in terms of x and y, we can describe the velocity components in a flow field effectively.
Examples & Analogies
Picture a map of a city (the x and y coordinates). The routes the cars take are analogous to stream functions guiding their movement through various streets, showing how traffic flows around buildings.
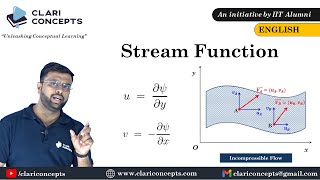
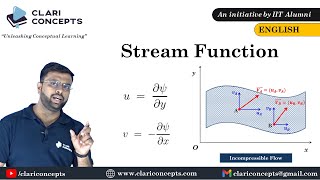
Relationship Between Velocities and Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I convert these two-dimensional equations to of u and v to dependent variables of scalar velocity component instead of two velocity components if I use a only a single dependent variables then my problems will be sorted out.
Detailed Explanation
Here, the focus is on the relationship between the velocity components (u and v) and the stream function. By linking the velocities in their respective directions to the derivatives of the stream function, this conversion simplifies the calculations needed for flow analysis.
Examples & Analogies
Think of it like summarizing a long report into key bullet points. By focusing on critical highlights (single dependent variable), it's easier to grasp everything at once, just as stream functions allow for simplified flow analysis.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stream Functions: Mathematical tools used to represent fluid flow in two-dimensional systems.
-
Compressible Stream Functions: Function variants that account for fluid density variations.
-
CFD Visualization: Application of stream functions in computational fluid dynamics for visual representation of flow patterns.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Visualizing airflow around an F-16 fighter jet helps illustrate compressible flow concepts via numerical simulations.
-
Flow around rotating cylinders is analyzed using injectables like air bubbles to visualize unsteady streamlines.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In flow that's dense, don’t you fret, Stream functions show the paths we get!
📖 Fascinating Stories
-
Imagine a river (the flow) with rocks (the barriers), streamlines are the little boats navigating between them, showing us how water flows.
🧠 Other Memory Gems
-
S.F. - Simplify Flow: Remember that stream functions help simplify complex fluid flow equations.
🎯 Super Acronyms
C.F.S. - Compressibility, Fluid Patterns, Simpler Equations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stream Function
Definition:
A mathematical function that simplifies the analysis of fluid flow by representing streamlines and allowing conversion of dependent variables.
-
Term: Compressible Flow
Definition:
Fluid flow in which density changes significantly throughout the flow field.
-
Term: CFD (Computational Fluid Dynamics)
Definition:
The use of numerical analysis and algorithms to solve and analyze problems involving fluid flows.