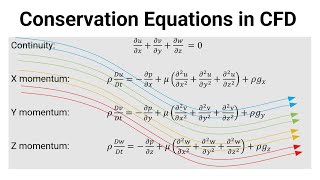
Conservation of Equations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stream Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning, everyone! Today, we are delving into the concept of stream functions in fluid mechanics. To start, can anyone explain why we need to simplify fluid flow equations?

Maybe because fluid dynamics can be quite complex?

Exactly! Stream functions help us manage this complexity. By using stream functions, we can reduce our equations from two dimensions into one, making them much easier to solve. Can anyone think of a scenario where this simplification is particularly useful?

In simulations, like those used for airplanes or vehicles?

Absolutely! Let's remember the acronym 'SIMPLE' - *S*implifying complex calculations, *I*ntegrating properties of fluids, *M*odeling flow patterns, *P*redicting behaviors, *L*earning from simulations, *E*ducation in fluid mechanics.*

That's a great way to remember it!

Great! So, we see stream functions are pivotal in CFD applications. At the end of this session, what do we conclude about stream functions?

They simplify our analysis of fluid flow!
Deriving Stream Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s derive how stream functions relate to velocity components. Remember, in incompressible flow, the mass conservation equation simplifies to the divergence of velocity being zero. Can anyone compute u and v from the stream function?

We can use the partial derivatives to find u as the gradient of stream functions!

Correct! So for a stream function ψ, how does the relationship to these velocities look?

u is ∂ψ/∂y and v is -∂ψ/∂x.

Exactly! Remember *PV=ψ* for interpreting flow visually. If we see acceleration, we identify changes in streamlines. Why is this relationship practical?

It helps in understanding vortex flows!

Smart! In our next session, we'll analyze vortex flows in detail. Could someone summarize what we just learned?

We learned how to derive u and v using stream functions, and the significance of these relationships.
Applications in Computational Fluid Dynamics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's talk about practical applications of stream functions. How do CFD tools like ANSYS Fluent enhance our understanding of fluid dynamics?

They allow us to visualize flow patterns, right?

Right! Flash back to our F-16 jet discussion - how do we interpret those streamline patterns?

Different colors represent different velocities, showing how the air flows around the jet!

Excellent observation! We can see there are both low and high-velocity zones. Remember, when streamlines converge, velocity increases, and they diverge, it decreases. Let's remember 'ASK' - *A*pplying CFD tools, *S*imulating real-world flow, *K*nowing the results!

Got it, the flow patterns tell us about zones of acceleration and deceleration!

Well said! Before we proceed, could someone summarize the main point of CFD applications?

CFD tools help us visualize complex flow patterns and velocity distributions in real-world scenarios like aircraft design.
Velocity and Pressure Relations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, how do velocity and pressure relate within stream functions? Recall Bernoulli’s equation; how does it help elucidate strong flow?

It informs us about energy conservation in the fluid, right?

Exactly! Where can we apply these equations effectively?

In regions with less friction, so near the streamlines!

Exactly! And by understanding this relationship, we can predict pressure variations effectively. Remember to visualize fluid motion as an 'EXPRESS' - *E*xplaining energy conservation, *X*periencing pressure differences, *P*redicting flow characteristics, *R*elating velocity to pressure, *E*mpowering design and simulations, *S*implifying complex systems.

That’s a powerful acronym! It'll help me remember how velocity and pressure interact.

Fantastic! To wrap up, can we summarize what we learned about the relation of velocity and pressure?

We learned that Bernoulli’s equation aids in understanding energy conservation, crucial for predicting fluid behavior in low-friction areas.
Summary and Review
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To wrap up our sessions, could we summarize everything we’ve discussed about stream functions?

Stream functions allow us to simplify complex equations in fluid dynamics.

They relate velocity and pressure gradients, and are essential for CFD applications in predicting fluid behavior around structures.

They also help visualize flow patterns, making it easier to understand zones of acceleration and deceleration.

And using Bernoulli’s equation helps explain energy conservation in fluid motion.

Well summarized! Remember, grasping the concept of stream functions is key to mastering fluid mechanics. Let's keep the acronym **SIMPLE** in mind: *S*implifying calculations, *I*ntegrating properties, *M*odeling flow, *P*redicting behaviors, *L*earning from simulations, and *E*ducation in fluid mechanics. Keep practicing, and you will master this topic!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section focuses on stream functions in fluid mechanics, emphasizing their definition in two-dimensional and cylindrical coordinate systems. It outlines the importance of stream functions for simplifying fluid flow equations and explains their application in computational fluid dynamics (CFD) to analyze complex flow patterns, such as around structures and rotating bodies.
Detailed
Conservation of Equations
In fluid mechanics, stream functions serve as critical tools for analyzing fluid flow. A stream function provides a method to simplify equations governing two-dimensional (2D) flow characteristics. This section elaborates on the concept of stream functions, their significance, and applications, all of which enhance understanding of fluid dynamics.
Key Points:
- Definition and Significance: Stream functions are introduced to manage the complexity encountered in traditional flow equations by transforming two dependent variables (u and v velocities) into a single variable, which facilitates the conservation of mass equations being simplified to one dimension in two-dimensional flow situations.
- Applications: Stream functions are particularly useful when applied to computational fluid dynamics (CFD) simulations, providing insights into flow patterns around objects like fighter planes and rotating cylinders. The use of software tools such as ANSYS Fluent allows visualization of intricate streamlines.
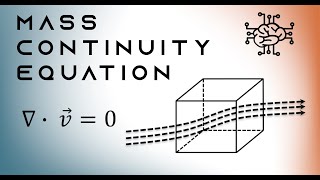
- Equations and Relationships: In incompressible flow, the mass conservation equations state that the divergence of the velocity should be zero. The relationship between the velocity components and stream functions is established through partial derivatives, simplifying calculations and enhancing the interpretation of flow behaviors.
- Two-dimensional and Cylindrical Coordinates: The discussion evaluates the applicability of stream functions across different coordinate systems, extending their use beyond basic 2D flows, including unattached flows associated with compressible fluids.
- Analytical Examples: Practical examples are provided to demonstrate the derivation and analysis of fluid flow using stream functions, embedding theoretical concepts into real-world applications.
Youtube Videos
![Conservation of mass (a.k.a., continuity) [Fluid Mechanics #2]](https://img.youtube.com/vi/PFgiW7P6omE/mqdefault.jpg)





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Stream Functions
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In fluid mechanics, the concept of a stream function is introduced to simplify the analysis of fluid flow. By defining a stream function, you can relate it to the velocity components of a fluid in a way that helps satisfy conservation equations.
Detailed Explanation
Stream functions are useful because they reduce the complexity of the equations involved in fluid flow. In a two-dimensional flow, the velocity components can be expressed in terms of a single function known as the stream function. This function helps ensure that the continuity equation, which expresses the conservation of mass, is automatically satisfied. Thus, when using stream functions, we derive velocity components directly from it, simplifying our calculations.
Examples & Analogies
Think of stream functions like the patterns in which dancers move across a dance floor. Each dancer represents a particle of fluid, and the overall pattern created by their movements reflects the flow of fluid. Just as dancers coordinate their movements to create smooth patterns, stream functions coordinate the velocity of fluid particles to ensure the mass of fluid remains conserved.
The Velocity Relationship
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The relationship between the stream functions and the velocity components can be defined mathematically. For a two-dimensional flow, the velocity in the x-direction, u, is equal to the partial derivative of the stream function with respect to y, and the velocity in the y-direction, v, is the negative of the partial derivative of the stream function with respect to x.
Detailed Explanation
This mathematical relationship can be expressed as follows:
- u = ∂ψ/∂y (where ψ is the stream function)
- v = -∂ψ/∂x.
This means if you have the stream function, you can easily find how fast the fluid is moving in any direction by taking its derivatives. This method not only simplifies calculations but gives a clear picture of how fluid flows in space, making it easier to visualize or simulate the flow patterns.
Examples & Analogies
Imagine you're reading a map of a river. The stream function is like the contours of the river, and the velocity components are the speed boats moving in the river. By understanding the contours (the stream function), you can predict how fast and in which direction each boat is likely to go, rather than trying to measure each boat's speed directly.
Mass Conservation and the Continuity Equation
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In essence, the principle of mass conservation in fluid dynamics states that the mass flow rate must remain constant from one cross-section of a flow to another, which leads to the continuity equation: The sum of mass fluxes into a control volume must equal the sum of mass fluxes out.
Detailed Explanation
The continuity equation is a fundamental principle in fluid dynamics. It can be simply expressed as the divergence of the velocity field being equal to zero for incompressible flows. Mathematically, this means that the rate of mass entering a control volume must equal the rate of mass leaving that volume. In practical terms, we can predict how fluid flows through varying cross-sections of a channel or pipe by applying this equation, ensuring that the same amount of fluid flows through each section over time.
Examples & Analogies
Consider an airport security line where a certain number of people enter the line every minute and the same number exit. If the line is narrower at one point, people must move faster to accommodate the same flow of customers. Just like the flow of blood in arteries must remain consistent, so must the flow of air through different parts of a ventilation system, as described by the continuity equation.
Applications of Stream Functions
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Stream functions can be used for various applications in fluid dynamics. Not only can they model two-dimensional incompressible flows, but they can also handle more complex scenarios like three-dimensional or compressible flows by applying appropriate modifications to the stream function definitions.
Detailed Explanation
The versatility of stream functions allows engineers and scientists to solve various complex problems in fluid dynamics. For instance, they can model flows around objects by modifying the stream function to fit the conditions of the flow, such as density changes or compressibility factors. The ability to analyze fluid systems in different configurations enhances the understanding of flow behavior in real-world applications, like aircraft design or pipeline systems.
Examples & Analogies
Think of stream functions as a flexible toolkit: just as a specialist can use different tools from their toolbox for various tasks, engineers can adjust stream function equations to suit different fluid flow problems, whether it be for designing more efficient aircraft wings or predicting how pollutants disperse in water systems.
Key Concepts
-
Stream Function: A tool for simplifying fluid equations into one dimension.
-
Velocity and Partial Derivatives: Relationship is defined via stream functions.
-
CFD Applications: Use of software to visualize fluid flow complexities.
-
Pressure Gradients: Relation to velocity in less frictional areas.
Examples & Applications
Deriving velocity components from a given stream function by calculating the necessary partial derivatives.
Using CFD software to simulate and visualize flow around an F-16 fighter plane.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When streams flow without a fuss, it's the function guiding us.
Stories
Imagine a river runs smoothly, its path decided by an unseen guide - the stream function that simplifies its course.
Memory Tools
Remember 'SIMPLE' to recall key features: Simplifying calculations; Integrating properties; Modeling flows; Predicting behaviors; Learning through simulations; Educating in fluid mechanics.
Acronyms
Use 'VEL' to remember Velocity, Energy, and Loss in the context of Bernoulli's principles.
Flash Cards
Glossary
- Stream Function
A mathematical function used in fluid dynamics to describe the flow of incompressible fluids.
- Velocity
A vector quantity that represents the rate of change of position in a given direction.
- Bernoulli's Equation
A principle that describes the conservation of energy in a flowing fluid.
- Divergence
A measure of the rate at which a quantity spreads out from a point.
- Computational Fluid Dynamics (CFD)
A branch of fluid mechanics that utilizes numerical analysis and algorithms to solve fluid flow problems.
Reference links
Supplementary resources to enhance your learning experience.
