Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stream Functions
Unlock Audio Lesson
Good morning, everyone! Today, we will explore stream functions and how they help us understand fluid flow. A stream function is a crucial mathematical concept that allows us to simplify fluid dynamics problems.
What exactly does a stream function do?
Great question! Stream functions relate to the flow field of a fluid, turning complex equations into simpler scalar equations. This helps us analyze flows without dealing with too many variables at once.
So, they make it easier to see how fluids move?
Exactly! Through visualization, stream functions let us see flow patterns, which is helpful for engineers. Remember, where you have streamlines close together, the flow is faster – that's a key point!
Can you give us an example of where they’re used?
Sure! When analyzing the airflow around an F-16 fighter jet, CFD software visualizes the streamlines and helps identify areas of high velocity and potential turbulence.
That sounds complex but interesting!
It can be, but stream functions help simplify these analyses. In our next session, we'll discuss the mathematical relationships involving stream functions.
Mathematical Formulation of Stream Functions
Unlock Audio Lesson
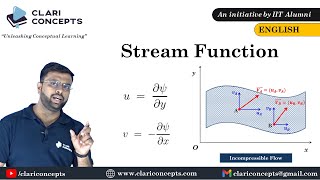
Now, let’s dive into the math! The relationships between stream functions and the velocity components u and v in a two-dimensional flow are key.
How do we express those relationships?
For incompressible flow, the velocity components can be expressed as u equal to the partial derivative of the stream function with respect to y, and v being the negative of the partial derivative with respect to x. Write this down as: u = ∂ψ/∂y, v = -∂ψ/∂x.
Why do we need to consider both u and v?
Both components are necessary because they represent the flow in different directions. The combination allows us to fully describe how a fluid moves in two dimensions.
And this applies to compressible and incompressible flows, right?
Correct! However, for compressible flows, adjustments in the equations for mass flux, incorporating density, are necessary.
That makes sense, so we need to be aware of when to use which equations?
Exactly! It’s crucial for solving complex problems. In our next session, we will discuss visualizing these concepts with real-world examples.
Real-World Applications of Stream Functions
Unlock Audio Lesson
Now let's connect theory to practice! Stream functions are extensively used in CFD. Can anyone explain how we visualize flows using CFD?
I think it’s like creating a simulation of how a fluid would move, right?
Exactly! We use simulations to visualize flow patterns around objects, such as buildings or aircraft. For an F-16, we can see how the air moves over its surface.
That helps engineers design better planes.
Right! The insights gained from these simulations can inform design tweaks to enhance performance and minimize drag. Remember, this all relates back to our understanding of streamlines.
So, the patterns can tell us where to expect turbulence?
Yes, and understanding these patterns is vital for prediction and control of flow in many applications.
Can we apply this knowledge to other flows too?
Absolutely, from non-aerodynamic flows in storage tanks to waterflow in piping, stream functions are versatile! In our next session, we’ll work on some exercises to cement your understanding.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The main focus of this section is on stream functions, including their definition and application in both compressible and incompressible flow, as well as their utility in understanding fluid dynamics through visualization using CFD software. The section emphasizes the importance of stream functions for analyzing two-dimensional flow and provides a review of related principles such as continuity equations.
Detailed
Stream Functions Basics
This section delves into the concept of stream functions in fluid mechanics, essential for understanding fluid dynamics. A stream function is a mathematical tool that represents flow patterns, allowing us to visualize how fluid behaves around objects and in complex flows. In this context, the lecture discusses the use of Computational Fluid Dynamics (CFD) tools, particularly in simulating flow patterns around objects like F-16 fighter jets and rotating cylinders.
Key Concepts Include:
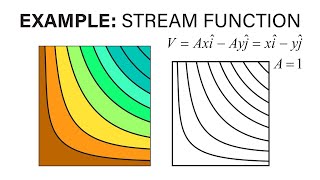
- Definition and Applications of Stream Functions: A stream function relates to the velocity field of a fluid flow, allowing us to convert complex equations involving two velocity components (u, v) into a single equation that represents the stream function. This simplifies problems, particularly in cases of incompressible flow.
- Interpretation of Streamlines: Streamlines are the paths traced by particles of the fluid, and they can't cross one another, implying conservation of mass as represented by volumetric flux. The section also covers how the density and proximity of streamlines indicate variations in flow speed, helping us identify areas of acceleration and deceleration within the flow.
- Mathematical Formulation: The lecture discusses how the derivatives of stream functions are related to fluid velocity components, filling out continuity equations. For incompressible flow, the divergence of the velocity field equals zero whereas for compressible flows, adjustments are made accounting for density.
- Visualizations of Flow: Various practical scenarios using CFD, including the flow patterns around buildings and rotating cylinders, are used to make the cases more tangible, underlining how stream functions aid in analyzing these flows.
Overall, understanding stream functions equips students with essential tools for tackling complex fluid dynamics issues, simplifying otherwise intricate equations, and effectively visualizing the behavior of fluids in motion.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So today I will be very basic way we will talk about what is the stream functions okay and we will talk about that in a two-dimensional coordinate systems we can have the stream functions.
Detailed Explanation
Stream functions are essential tools in fluid mechanics, particularly for describing fluid flow in two dimensions. They help simplify complex equations governing fluid motion by reducing the number of variables we need to consider. Instead of tracking multiple velocity components, stream functions allow us to represent fluid flow using a single function that can yield important velocity information.
Examples & Analogies
Think of stream functions like an artist creating a painting. Instead of focusing on every single brushstroke (which would be analogous to tracking every detail of the fluid's velocity), the artist focuses on the overall picture, using broad strokes to convey flow and motion. Just as the artist simplifies their work with fewer brushstrokes, engineers simplify fluid flow analysis with stream functions.
Understanding Streamlines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at the streamlines, as you know it, let I take a very simple examples. There is a hump or you can say it is a buildings okay, there is a big buildings are there and you have a uniform stream flow.
Detailed Explanation
Streamlines are visual representations of fluid flow paths. If you imagine placing a streamer or ribbon in flowing water, the path it takes illustrates the streamline. Stream functions can mathematically describe these streamlines, allowing us to understand how fluid moves around obstacles, such as buildings or humps. The flow will bend around these objects, creating patterns that can be predicted through calculations.
Examples & Analogies
Imagine a runner navigating around a series of cones on a track. As the runner approaches each cone, they need to change direction smoothly to continue running without losing speed. Similarly, streamlines represent how fluid must navigate around obstacles, showing us the natural paths fluids take in their environment.
Velocity and Pressure Gradients
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Along the streamlines we can see the velocities. Similar way we can get a pressure gradients act on the streamlines which looks is very complex figures here.
Detailed Explanation
In fluid mechanics, the velocity at various points along the streamline can change based on pressure gradients. Where the fluid flows faster, we can expect lower pressure, and where it flows slower, higher pressure. This principle is key in understanding how forces act on an object as it moves through a fluid, which can affect its stability and performance.
Examples & Analogies
Consider riding a bicycle. As you pedal faster (equating to higher fluid velocity), you feel less wind resistance (lower pressure). However, if you slow down, the air feels thicker against you (indicating higher pressure). This concept of pressure and velocity working together is crucial to both cycling and fluid dynamics.
Mass Conservation with Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Basic mass conservation equations and Bernoulli's equations to solve the problems.
Detailed Explanation
Mass conservation in fluid flow asserts that the mass of fluid entering a system must equal the mass exiting the system if there is no accumulation. This principle is encapsulated in the continuity equation. When applied with Bernoulli's equation, which relates pressure, velocity, and height in a fluid flow, we can effectively analyze fluid behavior in various scenarios using stream functions.
Examples & Analogies
Think of a water park slide. The amount of water entering the slide must equal the amount of water exiting it. If too much water flowed in, the slide would overflow. Just as water must be conserved, using stream functions allows us to analyze how fluids behave without losing track of essential mass flow aspects.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stream Functions: Functions that represent flow patterns in fluid dynamics by allowing the conversion of multi-variable equations into simpler forms.
-
Continuity Equation: A fundamental expression in fluid mechanics that ensures mass conservation in a fluid flow.
-
Visualizing Flow Patterns: The use of computational fluid dynamics to obtain insights into complex flow behaviors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An F-16 fighter jet simulation showing airflow patterns around its wings.
-
Flow visualization around cylindrical objects to study vortex dynamics.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Stream function's flow, a path we can show, helps us simplify what we need to know.
📖 Fascinating Stories
-
Imagine a river flowing around a bend; the water’s path drawn by invisible lines shows us how to understand the currents.
🧠 Other Memory Gems
-
S.F. - Simplifies Flow; Stream Functions streamline fluid flow analysis.
🎯 Super Acronyms
SFT - Stream FUNCTION Transitions
- from complex equations to simpler forms.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stream Function
Definition:
A scalar function whose contours represent the streamlines of a flow, simplifying fluid dynamics equations.
-
Term: Streamlines
Definition:
Imaginary lines that represent the trajectory of fluid particles in a flow field; no fluid crosses these lines.
-
Term: CFD (Computational Fluid Dynamics)
Definition:
A branch of fluid mechanics that uses numerical analysis and algorithms to solve and analyze problems involving fluid flows.
-
Term: Continuity Equation
Definition:
A mathematical expression that represents the conservation of mass in a fluid flow.
-
Term: Incompressible Flow
Definition:
A flow regime in which fluid density is considered constant.
-
Term: Compressible Flow
Definition:
A flow regime in which fluid density can change significantly due to variations in pressure or temperature.