Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stream Functions
Unlock Audio Lesson
Good morning, everyone! Today we're going to discuss stream functions and their role in fluid flow analysis. Can anyone explain what they understand by stream functions?
I think they are some kind of mathematical function that helps us understand fluid flow.
Exactly! Stream functions are tools that help us visualize the flow of fluids by reducing the number of dependent variables. We can use them to derive velocity components from a single function. Can anyone tell me why this might be useful?
It simplifies the calculations, making it easier to analyze complex flows, right?
Absolutely! Let’s remember that reducing variables generally leads to simpler solutions. A mnemonic to keep this in mind is 'SIMPLE': Stream functions Increase Mathematical Precision and Lower Errors!
Mathematical Derivation of Stream Functions
Unlock Audio Lesson
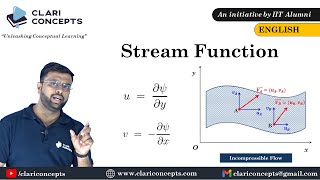
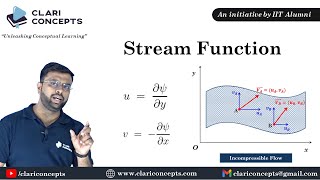
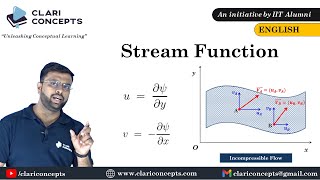
Let’s dive into how we mathematically derive stream functions from velocity components. The velocity components u and v in a two-dimensional flow can be expressed as the gradients of the stream function. Can anyone express how we represent these relationships?
Isn't it that u equals the partial derivative of psi with respect to y, and v is the negative partial derivative with respect to x?
Exactly right! We use these relationships to satisfy the continuity equation, meaning the flow is conserved. Let’s do a small exercise: if u = 2xy and v = -x² + y, can we find the corresponding stream function?
We can integrate these relationships!
Correct! Remember, the stream function streamlines the flow analysis. To help remember these derivatives, think of the acronym 'PUIS': Partial derivatives yield u and v from psi!
Applications of Stream Functions in CFD
Unlock Audio Lesson
Now let’s discuss practical applications of stream functions in CFD. We often visualize complex flows, such as those around airplanes. How might stream functions help in those cases?
They could help visualize the flow around surfaces and help us understand how fast the fluid is moving.
Exactly! By plotting streamlines, we can easily identify high and low-velocity zones. This helps in designing more efficient planes. Can we think about a military aircraft like the F-16? What unique challenges might arise?
Turbulence in airflow due to complex shapes could make things tricky.
Good insight! Turbulence models are crucial in such simulations. Remember, analyzing flow requires an understanding of stream functions for accuracy. A helpful memory rhymes: 'Streamlines flow in a line, where calculations become divine!'
Incompressible vs. Compressible Flow
Unlock Audio Lesson
Finally, let's differentiate how stream functions apply in incompressible and compressible flows. Can anyone explain this difference?
Incompressible flow maintains constant density, while compressible flow deals with variations in density.
Exactly! For incompressible flows, we have a simple divergence condition, but with compressible flows, we introduce density variations. To remember this, think of 'IDEAL': Incompressible Density Equal Always Low.
That's a clever way to remember it, thanks!
Great! So keep these distinctions in mind as they are critical for your analysis in fluid mechanics. Understanding stream functions enables us to solve mass conservation equations efficiently, be it in incompressible or compressible scenarios.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Stream functions are introduced as a mathematical tool to simplify fluid flow analysis by reducing dependent variables. This section elaborates on the derivation of stream functions, their significance in solving continuity equations, and their application in both incompressible and compressible flows, with practical examples provided for better understanding.
Detailed
Derivation of Stream Functions
In fluid mechanics, stream functions offer a powerful mathematical approach to simplify the analysis of fluid flow. By defining stream functions, we can reduce the number of dependent variables typically involved in analyzing fluid flow. In this section, we delve into the derivation of these functions and discuss their practical applications in multiple scenarios, including two-dimensional, incompressible, and compressible flows.
Key Concepts
The concept revolves around defining a stream function for two-dimensional flows, which is a function of both x and y coordinates. In understanding complex flows, especially around structures like buildings or fighter jets, streamlines can be effectively utilized. Through computational fluid dynamics (CFD) software, we visualize these streamlines, which exhibit velocity variations and pressure gradients in the fluid.
- Streamlines and Stream Functions: Stream functions are defined as functions that represent the family of curves known as streamlines, where each streamline corresponds to a constant value of the stream function.
- Mathematical Representation: The velocity components are represented by the gradients of the stream function, leading to a more straightforward solution of flow equations.
- Applications in CFD: Stream functions are utilized to observe fluid behavior in various applications, such as simulating airflow around aircraft or other moving objects.
- Importance in Mass Conservation: They satisfy the continuity equations, ensuring that mass is conserved within the flow field, which is crucial in both incompressible and compressible flow scenarios.
In summary, the understanding of stream functions not only simplifies the equations of fluid flow but also enhances our ability to visualize and analyze complex flow patterns using modern computational tools.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us go very basic of the streamline and stream functions which is essential for undergraduate students that part what I will cover it. So today I will be very basic way we will talk about what is the stream functions okay and we will talk about that in a two-dimensional coordinate systems we can have the stream functions. We also talk about compressible stream functions not only incompressible functions and we will also talk about cylindrical coordinate systems and then we will also solve some examples.
Detailed Explanation
In this chunk, we introduce the concept of stream functions, which are essential for analyzing fluid flow. Stream functions are particularly significant in two-dimensional flow scenarios. They help us visualize streamlines, which represent the path that fluid particles follow. In fluid mechanics, we can have different types of stream functions, such as those applicable for incompressible and compressible fluids. Additionally, we can utilize stream functions in various coordinate systems, including cylindrical coordinates. Understanding these concepts is crucial for solving fluid flow problems effectively.
Examples & Analogies
Think of stream functions like a map for a river. Just as a river map shows the path the water takes, stream functions visualize how fluid moves through space. If you imagine the water flowing evenly down a street, the streamlines represent the path of the water, guiding us to see where the water is fast and where it slows down.
Deriving Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at the stream functions, as you know it, let I take a very simple examples. There is a hump or you can say it is a buildings okay, there is a big buildings are there and you have a uniform stream flow, uniform stream flow. So if want to draw a streamlines will go like this, go like this, go like this. So these are the streamlines we can artistically draw. With knowledge of the stream lines how the flow behaviors will happen or how the virtual fluid balls just assuming it that a series of balls are there which is coming in uniform speed okay. Let be the v speed how the balls will move it with time that is what I given the examples how the balls are moving it that is what you can visualize it okay.
Detailed Explanation
In this section, we illustrate how to draw streamlines based on a hypothetical example of airflow over a building. When airflow meets an obstacle like a building, the streamlines need to adjust, bending around the structure. By imagining the flow as a set of virtual fluid balls, we can visualize how the flow dynamics change in the presence of various shapes. Understanding how these 'balls' move helps us predict flow patterns, which is crucial for engineers when designing around structures or assessing environmental impacts.
Examples & Analogies
Imagine throwing marbles in a straight line towards a wall. As they reach the wall, they will curve around it. In the same way, airflow behaves when it encounters a building; the streamlines curve around the building instead of going straight. Visualizing airflow as marbles helps us comprehend how obstacles change the flow's direction and speed.
The Concept of Conservation in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So now we are emphasizing the regions where there is less frictional force. For example, the streamlines if I am not taking closer to these structures, closer to these buildings no doubts I will not have this frictional force it will be dominated. So I can have a basic mass conservation equations and Bernoulli's equations to solve the problems.
Detailed Explanation
This segment introduces two foundational principles in fluid mechanics: mass conservation and Bernoulli’s equation. Mass conservation refers to the principle that mass cannot be created or destroyed within a closed system. When analyzing flow around structures, we recognize areas with less friction allow for more straightforward application of these principles. By identifying these low-friction zones, we can more easily employ Bernoulli’s equation, which relates pressure and velocity in a streamline, to solve fluid flow problems effectively.
Examples & Analogies
Consider a water slide; where the slide is smooth and straight (low friction), water flows down rapidly. But if the slide has many sharp turns or bumps (increased friction), the water slows down. In similar fashion, in fluid problems, identifying low-friction regions helps us understand how fluids will flow and where we can apply conservation principles.
Mathematical Representation of Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I convert these two-dimensional equations to of u and v to dependent variables of scalar velocity component instead of two velocity components if I use a only a single dependent variables then my problems will be sorted out.
Detailed Explanation
In this part, we discuss how to simplify the mathematical modeling of fluid flow by utilizing stream functions. By reducing the two independent variables of velocity (u and v) into a single function (the stream function), we can streamline our calculations. This transition makes it easier to apply the continuity equations without losing essential details of the flow behavior, allowing for a more manageable approach in solving fluid dynamics problems.
Examples & Analogies
Think of organizing your notes for studying. Instead of having several papers with different sections, you create one comprehensive guide. By condensing your notes into a single, well-organized format, you make studying more straightforward and efficient, much like how stream functions simplify our calculations in fluid mechanics.
Application to Complex Flows
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at very interesting flow which is having a vortex as you open up a bathtub or water tap you can see the vortex and or you can see the larger vortex which is there in a cyclones. Many of complex flow we define as a vortex flow.
Detailed Explanation
Here we address more complex flow patterns like vortices, which occur in situations such as draining water or cyclones. Vortex flows are characterized by circular motion and complex interactions within the fluid. Recognizing and defining these flows as vortex flow is significant since it allows us to develop specific equations and streamline methods that model these dynamics with high accuracy. In engineering, understanding vortices is crucial for predicting behavior in various applications, from designing buildings to aircraft.
Examples & Analogies
Imagine the swirling motion of water when draining a sink. This swirling motion creates a vortex where the water spins around a central point. Recognizing this whirlpool effect helps engineers design better plumbing systems and understand how different shapes can control or influence the flow of fluids.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
The concept revolves around defining a stream function for two-dimensional flows, which is a function of both x and y coordinates. In understanding complex flows, especially around structures like buildings or fighter jets, streamlines can be effectively utilized. Through computational fluid dynamics (CFD) software, we visualize these streamlines, which exhibit velocity variations and pressure gradients in the fluid.
-
Streamlines and Stream Functions: Stream functions are defined as functions that represent the family of curves known as streamlines, where each streamline corresponds to a constant value of the stream function.
-
Mathematical Representation: The velocity components are represented by the gradients of the stream function, leading to a more straightforward solution of flow equations.
-
Applications in CFD: Stream functions are utilized to observe fluid behavior in various applications, such as simulating airflow around aircraft or other moving objects.
-
Importance in Mass Conservation: They satisfy the continuity equations, ensuring that mass is conserved within the flow field, which is crucial in both incompressible and compressible flow scenarios.
-
In summary, the understanding of stream functions not only simplifies the equations of fluid flow but also enhances our ability to visualize and analyze complex flow patterns using modern computational tools.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Visualizing airflow around an F-16 fighter jet using stream functions to analyze turbulence and velocity changes.
-
Applying stream functions to model flow through a rotating cylinder to observe vortex formation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Streamlines flow in a stream, helping us visualize the dream!
📖 Fascinating Stories
-
Imagine a calm river where each leaf represents a streamline, carrying with it the secret of fluid movement.
🧠 Other Memory Gems
-
Use 'STREAM' to remember: 'Simplify Timely Relationships for Effective Analysis of Motion.'
🎯 Super Acronyms
Use 'PSI' to remember
- 'Partial derivatives yield Stream functions for Incompressible flow.'
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stream Function
Definition:
A scalar function whose partial derivatives give the components of velocity in a two-dimensional flow field.
-
Term: Streamlines
Definition:
Curves that represent the flow of fluid particles, indicating the path that fluid elements follow over time.
-
Term: Continuity Equation
Definition:
A mathematical expression that represents the conservation of mass in fluid dynamics.
-
Term: Incompressible Flow
Definition:
A flow regime where the fluid density remains constant.
-
Term: Compressible Flow
Definition:
A flow regime where changes in fluid density significantly affect the flow.