Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stream Functions
Unlock Audio Lesson
Good morning, everyone! Today we're going to cover stream functions, a vital concept in fluid mechanics. Can anyone tell me what they understand by stream functions?
Isn't a stream function a way to represent fluid flow lines?
Exactly! Stream functions help us visualize the flow patterns, known as streamlines. They represent the velocity field of the flow. By using them, we can simplify our equations.
How do they simplify things?
Great question! By using stream functions, we can turn two velocity components into a single function, which helps in analyzing the flow better. Let's remember this using the acronym 'SIMPLIFY' — Stream functions Integrate Motion and Present Liquid flow with Increased Flow yield.
Does this work for both incompressible and compressible flows?
Yes! For both types of flows, stream functions can be defined. We'll dive deeper into how we derive the velocity components from these functions.
Velocity Components from Stream Functions
Unlock Audio Lesson
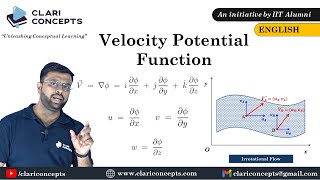
Let's focus on how we derive the velocity components from stream functions. If we have a stream function Ψ, can anyone express how to find the velocities u and v?
I think u is related to the partial derivative of Ψ with respect to y?
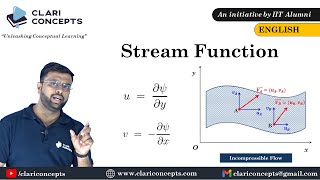
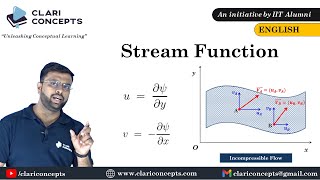
Correct! u is given by the equation u = ∂Ψ/∂y. And how do we find v?
It’s the negative partial derivative of Ψ with respect to x, right? So v = -∂Ψ/∂x?
Well done! Remember, these relationships are crucial for analyzing two-dimensional flows. Let’s use the mnemonic to remember this: 'Y Gives Up, X Goes Down' – this stands for 'Y-gradient gives u, X-gradient gives negative v.'
What happens if the fluid is compressible?
That's an important consideration! We can still use stream functions. In compressible flows, we incorporate density into our equations.
Applications of Stream Functions
Unlock Audio Lesson
Now that we've understood the theory, let’s apply our knowledge to real-world scenarios. For instance, how would you visualize the airflow around an F-16 fighter jet using stream functions?
We could plot the streamlines to show where the airflow is most concentrated and how fast it's moving!
Exactly! CFD tools like ANSYS allow us to visualize these patterns effectively. It shows us the variation in velocities and pressure gradients. Can you recall why we care about these pressure gradients?
They can significantly impact the performance and stability of the aircraft!
Correct! This visualization helps us make critical engineering decisions. Remember this with the phrase 'Visualize to Optimize'—an important approach in design.
Generalization of Stream Functions
Unlock Audio Lesson
Let’s move on to how stream functions can be generalized. Can they also apply to axisymmetric flows?
Yes, they can! What about cylindrical coordinate systems?
Great point! In cylindrical systems, we adjust our definitions of the stream functions. They allow us to still maintain a single-variable approach in analyzing complex flows.
But do the formulas change?
The underlying principle remains the same, but the specific functions we use may vary depending on the flow characteristics. Remember: 'Adapt to Flow' – always tailor your approach based on the scenario.
Recap and Conclusion
Unlock Audio Lesson
As we wrap up, can anyone summarize what we've learned about stream functions today?
Stream functions simplify the analysis of fluid flow and allow us to derive velocity components from them!
And they’re applicable in many scenarios, including complex simulations like CFD for an aircraft!
Exactly! Stream functions are powerful tools in fluid mechanics, helping us visualize and solve problems more effectively. Keep the phrase 'Simplicity is Calculation' in mind, as it reminds us of the elegance behind using stream functions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the significance of stream functions in fluid mechanics, detailing how they help visualize fluid flows, especially in two-dimensional incompressible and compressible flows. It emphasizes the mathematical representation of velocity components derived from stream functions, alongside practical applications and examples.
Detailed
Detailed Summary
In this section, we delve into the fundamental concept of stream functions in fluid mechanics, which facilitate the analysis of fluid flows, particularly in two-dimensional systems. Stream functions are critical because they allow the reduction of complex flow equations into simpler forms, thus providing an effective means to visualize and solve fluid flow problems.
Stream functions are introduced to help us derive velocity components (u and v) in fluid dynamics effectively. For incompressible flows, the relationship between the stream function and fluid velocity can be expressed through partial derivatives. The section emphasizes that the gradient of the stream function in the y-direction gives the u component of velocity, while the gradient in the x-direction gives the v component (with a negative sign).
Moreover, the section illustrates practical applications through computational fluid dynamics (CFD) examples, such as the flow around an F-16 fighter jet and the flow due to rotating cylinders. These examples showcase how stream functions can help visualize complex flow patterns and highlight important behaviors like pressure gradients and turbulence.
Additionally, key equations, including mass conservation and Bernoulli’s equations, are reestablished to reinforce how stream functions are used to simplify the analysis of two-dimensional flow problems, both in compressible and incompressible scenarios. Stream functions remain foundational tools in understanding fluid dynamics, enabling engineers and scientists to model and predict flow behavior in various applications.
Youtube Videos
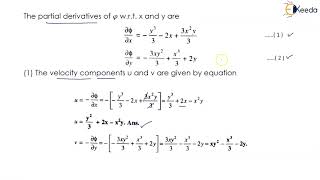
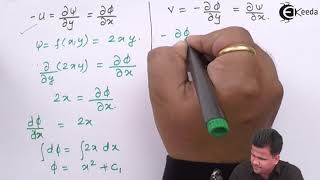
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us go very basic of the streamline and stream functions which is essential for undergraduate students that part what I will cover it. So today I will be very basic way we will talk about what is the stream functions okay and we will talk about that in a two-dimensional coordinate systems we can have the stream functions.
Detailed Explanation
This chunk introduces the concept of stream functions, which are essential for understanding fluid mechanics. A stream function is a mathematical representation of flow in a fluid, particularly in two-dimensional flow scenarios. It helps visualize how fluids move around boundaries such as buildings or other structures. In essence, the stream function simplifies the complexity of fluid flow analysis.
Examples & Analogies
Imagine watching water flow around a rock in a river. The flow lines represent how water moves around the obstacle, and we use stream functions to describe these patterns mathematically. This is similar to how virtual fluid balls can help visualize movement in a more complex environment.
Understanding Velocity Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I convert these two-dimensional equations to of u and v to dependent variables of scalar velocity component instead of two velocity components if I use a only a single dependent variables then my problems will be sorted out. That is what is a strategy was followed still has been followed to solve many of the fluid flow problems.
Detailed Explanation
In this chunk, the discussion revolves around transforming the analysis of fluid flow from two independent velocity components (u and v) to a single scalar velocity variable. This simplification allows for easier calculations and modeling of fluid behavior. By using a single dependent variable, engineers and scientists can solve complex fluid dynamics problems more efficiently.
Examples & Analogies
Think about simplifying your budget by combining all your expenses into one category. Instead of tracking every separate expenditure, you create a summary of your total spending. This makes it easier to understand overall financial health, similar to using a single equation to represent velocity in fluid dynamics.
Stream Function and Velocity Relationship
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, the basically how to draw the streamline how we can solve this two-dimensional equations where you have two dependent variables in u and v components. Unless otherwise we make it a single functions which is called the stream functions.
Detailed Explanation
This chunk highlights the relationship between stream functions and the velocity of fluid flow. The key takeaway is that the derivatives of the stream functions correspond to the fluid velocity components. Specifically, the gradient of the stream function in the y-direction gives the velocity in the x-direction and vice versa, signifying a direct relationship between the movement of fluid and its mathematical representation via stream functions.
Examples & Analogies
Consider a bicycle rider navigating through a park. The paths they take (streamlines) determine their speed and direction. The mathematical relationships from stream functions are like a map, helping to show the best routes based on varying terrains.
Mathematical Formulation of Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you look at the stream functions as we know the basic continuity equations again I am writing it because you need to remember only this part of equations okay which is too simple okay. You need not to remember different form of the continuity equations.
Detailed Explanation
This part reiterates the importance of understanding and correctly applying the fundamental continuity equations in fluid mechanics. These equations are essential for ensuring mass conservation within fluid systems. The discussion emphasizes simplicity, encouraging students to focus on key forms of equations necessary for mastering fluid dynamics.
Examples & Analogies
Think of continuity equations like a conservation law in a game of marbles. If you have a set number of marbles (mass) in play, the total cannot change; it can only move from one player's hand to another. Understanding how this works makes it easier to play the game effectively, just as grasping continuity helps navigate fluid equations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stream Functions: Essential for visualizing fluid flow and simplifying analysis.
-
Velocity Component Relationships: Derived from the stream functions to express fluid motion.
-
Applications in CFD: Used extensively for visualizing complex fluid flows in engineering.
-
Incompressible vs. Compressible Flows: Different fluid behaviors that can be analyzed using stream functions.
-
Pressure Gradients: Effects of pressure changes on flow behavior.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The airflow around an F-16 fighter jet can be visualized using stream functions to identify pressure zones and flow patterns.
-
In CFD simulations, stream functions help in understanding the complex flow behavior around rotating cylinders.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Streamlines flow, easy to see, helping u and v simplify with glee!
📖 Fascinating Stories
-
Imagine a fluid as a playful dancer, moving gracefully along the streamlines, where every twist and turn is captured by the stream function. Each position reveals the dance's speed, u and v.
🧠 Other Memory Gems
-
SIMPLE: Stream functions Integrate Motion, Present Liquid flow with Increased Flow yield.
🎯 Super Acronyms
FLOW
- Fluid Line Of Work
- as represented by stream functions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stream Function
Definition:
A mathematical function used to describe the flow of a fluid, where the streamlines of the flow are represented as constant values of this function.
-
Term: Velocity Components
Definition:
The individual components of fluid velocity in the x and y directions, often denoted as u and v.
-
Term: Incompressible Flow
Definition:
A flow in which the fluid density remains constant.
-
Term: Compressible Flow
Definition:
A flow where changes in fluid density are significant, typically occurring at high velocities.
-
Term: Pressure Gradient
Definition:
The rate at which pressure changes in a fluid, influencing fluid motion.
-
Term: CFD (Computational Fluid Dynamics)
Definition:
A branch of fluid mechanics that uses numerical analysis and algorithms to solve problems involving fluid flows.
-
Term: Mass Conservation
Definition:
A principle stating that mass cannot be created or destroyed in a closed system.