Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Flow and Stream Functions
Unlock Audio Lesson
Good morning, everyone! Today, we're going to dive into the concepts of fluid flow and specifically look at stream functions. Can anyone tell me what they understand by fluid flow?
Isn’t it the movement of liquid or gas? Like water flowing in a river?
Exactly right! Fluid flow refers to how liquids and gases move. Now, stream functions are a way we can analyze this flow mathematically. They help us understand complex flow patterns by reducing the number of variables we need to consider. Can anyone think of why simplifying equations would be important?
It makes solving problems easier, right? If we have fewer variables, it’s less complicated!
Correct! Simplifying our equations using stream functions allows us to focus on the flow characteristics without getting overwhelmed by complex interactions. Remember, stream functions lead to the depiction of streamlines which represent the flow path.
So, if we identify streamlines, we can predict how a fluid will behave?
That's right! Streamlines visually represent the paths that fluid particles will follow. At the end of this session, remember that stream functions are crucial tools for analyzing moving fluids.
Stream Functions and Pressure Gradients
Unlock Audio Lesson
Now that we understand stream functions, let's explore how they relate to pressure gradients in fluid mechanics. Can anyone explain what a pressure gradient is?
It sounds like the change in pressure over a distance, right?
Exactly! A pressure gradient is defined as the rate of change of pressure in a direction. High pressure will push fluid towards areas of lower pressure. How do you think this relates to flow patterns?
So, fluids will flow from high to low pressure areas, and that affects the flow's speed and direction?
Correct! The greater the pressure difference, the stronger the flow. Understanding this concept is essential for analyzing how fluid behaves around objects, such as buildings or aircraft. We can visualize these flows using CFD tools, demonstrating the impact of pressure gradients.
So, with CFD we can see how pressure affects flow around these objects?
Yes! CFD simulates fluid flow, and the visual outputs help us comprehend and predict fluid dynamics effectively.
Application of Stream Functions in CFD
Unlock Audio Lesson
Let's now discuss how we apply these concepts in Computational Fluid Dynamics or CFD. Who has experience with CFD tools?
I know some basic CFD tools but haven’t applied them yet.
No problem! CFD tools allow us to analyze flow patterns by simulating fluid behavior. For example, if we’re looking at airflow around an F-16 jet, we can visualize the streamlines and their respective velocities. Can anyone tell me what effect increasing speed might have on a plane’s lift?
Higher speed creates lower pressure above the wing, thus generating lift!
Exactly! And CFD helps us visualize these patterns, making it easier to predict performance. Remember the CFD outputs will display velocity and pressure distributions, showing us complex interactions. It’s fascinating how technology aids in understanding fluid flow, isn’t it?
Yes! It shows how everything is interconnected in real-world applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, key concepts of pressure gradients and flow patterns are explored, emphasizing the role of stream functions in representing and understanding fluid flow. Various examples, including CFD simulations of airflow around structures, showcase the application of these concepts in real-life scenarios.
Detailed
Detailed Summary
In this section, we delve into the fundamentals of pressure gradients and flow patterns within the realm of fluid mechanics. The discussion revolves around the utility of stream functions, particularly in visualizing and analyzing the dynamics of fluid flow. Stream functions simplify the study of two-dimensional flows by reducing the complexity of equations governing fluid dynamics.
The section begins by presenting applications of Computational Fluid Dynamics (CFD) and the visualization of flow patterns around bodies such as the F-16 fighter jet. Streamlines, which depict the trajectories of fluid particles, and their relationship with velocity patterns are introduced, explaining how different colors in visualizations indicate varying velocities.
Furthermore, the understanding of flow around obstacles, such as buildings, is expanded upon, showcasing how frictional forces can alter flow patterns and how the basic principles of mass conservation and Bernoulli's equations can be leveraged in less friction-dominated regions. The section also highlights how advancements in computational tools have enhanced our ability to analyze complex flow scenarios, underscoring the importance of stream functions in modeling both incompressible and compressible flows. By defining relationships between stream functions and velocity components, students learn to derive essential equations that govern fluid behavior.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us go very basic of the streamline and stream functions which is essential for undergraduate students that part what I will cover it. So today I will be very basic way we will talk about what is the stream functions okay and we will talk about that in a two-dimensional coordinate systems we can have the stream functions.
Detailed Explanation
This chunk introduces the concept of stream functions, which are a mathematical tool used to represent fluid flow in two dimensions. Stream functions help to visualize how fluid moves around obstacles or through various environments. When dealing with fluid mechanics, stream functions simplify complex equations by reducing the number of variables involved, which can aid in analyzing flow patterns.
Examples & Analogies
Imagine trying to understand the movement of a river. Instead of focusing on every single drop of water, you could use a map to show the general flow direction and speed of the water across the landscape. A stream function acts like that map, helping you visualize the larger picture without getting lost in the tiny details.
Core Equations and Models
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, the basically how to draw the streamline how we can solve this two-dimensional equations where you have a two dependent variables in u and v components. Unless otherwise we make it a single functions which is called the stream functions. If I convert these two-dimensional equations to of u and v to dependent variables of scalar velocity component instead of two velocity components if I use a only a single dependent variables then my problems will be sorted out.
Detailed Explanation
This chunk highlights the need to consolidate multiple dependent variables in fluid flow problems into a single stream function. In two-dimensional flow, instead of managing both 'u' and 'v' (the velocity components in the x and y directions), stream functions allow us to express these flows using a single variable. This simplification makes it easier to solve equations related to fluid motion, ensuring that the conservation of mass and momentum can be efficiently assessed.
Examples & Analogies
Think of stream functions like a single light switch that controls multiple bulbs in a room; instead of flipping each switch separately for each bulb, you can control them all at once. This makes it simpler when you want to adjust how bright the room is, just as using a stream function simplifies the fluid flow analysis.
Pressure Gradients and Their Effects
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
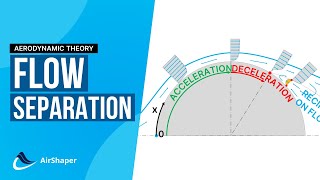
we can get a pressure gradients act on the streamlines which is looks is very complex figures here, very complex figures.
Detailed Explanation
This segment discusses how pressure gradients impact fluid flow along streamlines. A pressure gradient is the change in pressure with distance in a fluid. These gradients can create complex flow patterns, influencing how quickly or slowly the fluid moves. Understanding these gradients is crucial for applications like designing pipelines or understanding weather systems where varying pressure can lead to wind patterns.
Examples & Analogies
Imagine you're blowing air through a straw filled with marbles. If the straw is narrow (high pressure), and you blow harder, the marbles will shoot out more rapidly. If you were to widen the straw (lower pressure), the marbles may not move as quickly. The difference in pressure within the straw determines how the marbles (or fluid particles) behave—this mirrors how fluid moves in response to pressure gradients.
Applications of Computational Fluid Dynamics (CFD)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
nowadays the tools like ANSYS fluent or any CFD softwares available to visual the fluid flow, how it is happening it.
Detailed Explanation
This chunk emphasizes the role of modern Computational Fluid Dynamics (CFD) software, such as ANSYS Fluent, in visualizing and simulating fluidic behaviors in various scenarios. These tools allow engineers and scientists to model complex fluid interactions and pressure distributions accurately, thus aiding in designing vehicles, structures, and even predicting weather phenomena.
Examples & Analogies
Consider CFD software as an advanced video game where you can simulate and predict how a character (or in this case, fluid) moves through different environments. Just like in a game where you observe the effects of gravity, speed, or resistance, CFD lets you see how fluids behave under various conditions, helping to make effective design decisions.
Velocity Magnitudes and Flow Complexities
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
if you can look at very interestingly these figures that how the streamlines patterns are there on a fighter F-16 fighter jets. We are not going details what the turbulence models solved by the ANSYS fluent but I am just visualizing you that you try to look it.
Detailed Explanation
Here, the discussion revolves around observing how velocity magnitudes vary in complex flow scenarios, particularly around objects like fighter jets. The analysis of these patterns helps in understanding aerodynamic efficiency and the performance of the vehicle in different flight conditions.
Examples & Analogies
Think about how a bird flies through the air. The way air flows over its wings changes based on its speed and direction. By studying the patterns in which the air moves around the bird, we can improve airplane designs. Just like understanding a bird's flight is key to making better aircraft, studying velocity around jets helps us refine flying machines.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stream Functions: Used to simplify the analysis of fluid flow by reducing the number of dependent variables.
-
Pressure Gradients: Driving force of fluid movement from high to low pressure areas.
-
Computational Fluid Dynamics (CFD): Simulation tools that help visualize the behavior of fluid flows.
-
Streamlines: Visual representations of the flow path of fluid particles, important in understanding flow dynamics.
-
Bernoulli's Equation: Key equation that relates pressure, velocity, and height in fluid dynamics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An F-16 jet experiencing different airflow patterns during various flight maneuvers is analyzed using CFD to visualize how pressure gradients affect lift and drag.
-
Flow visualization around buildings helping engineers design structures to minimize wind resistance and optimize energy use.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Flow high to low, pressure’s the game, for streams to move, it's never the same!
📖 Fascinating Stories
-
Imagine a river flowing from a mountain (high pressure) to the valley (low pressure), just like fluids moving along their paths!
🧠 Other Memory Gems
-
S-P-C for Stream Functions, Pressure Gradient, and Computational Fluid Dynamics.
🎯 Super Acronyms
SPC - Stream Function, Pressure Gradient, CFD
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stream Function
Definition:
A scalar function whose contours represent streamlines in a flow field, simplifying the analysis of fluid mechanics.
-
Term: Pressure Gradient
Definition:
The rate of change of pressure in a given direction, influencing fluid flow direction and speed.
-
Term: Computational Fluid Dynamics (CFD)
Definition:
A computational technique used to simulate and analyze fluid flow using numerical methods and algorithms.
-
Term: Streamlines
Definition:
Lines that represent the path followed by fluid particles, showing the direction of flow at any point in a fluid.
-
Term: Mass Conservation
Definition:
The principle stating that mass in a closed system remains constant over time; essential in fluid dynamics equations.
-
Term: Bernoulli's Equation
Definition:
A principle that relates the pressure, speed, and height of a flowing fluid, useful in analyzing fluid flow.