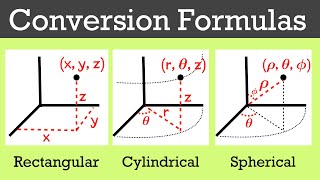
Cylindrical Coordinate Systems
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stream Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to explore what stream functions are and why they matter in fluid mechanics. Stream functions help us visualize fluid flow.

Can you explain what a stream function actually does?

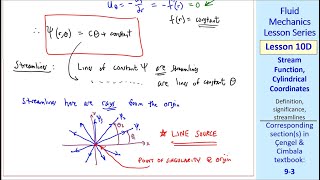
Certainly! A stream function is a scalar function whose contours represent the streamlines of fluid flow. In simpler terms, it helps us understand the flow pattern without calculating every point in the field.

So, if I plotted the stream function, I could see how the fluid is moving?

Exactly! And remember, when you have a continuous flow, the fluid doesn't cross streamlines, which is why they’re so useful.

How do we actually derive the velocities from these functions?

Great question! The velocity in the radial direction is the derivative of the stream function with respect to the angle, and the angular velocity is the negative derivative with respect to radius.

Got it! So, what about cases with compressible flow?

We can extend stream functions to compressible flows by incorporating density. This allows us to analyze a wider variety of flow scenarios.

To summarize, stream functions help visualize flow, allowing us to derive velocities and understand mass conservation better.
Applications of Stream Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand stream functions, let’s talk about how they’re applied in real-world scenarios, such as in Engineering using Computational Fluid Dynamics.

Can you give us examples of where this applies?

Sure! One prominent example is the flow around aircraft like the F-16 fighter jet. By using stream functions, we can simulate airflow patterns and ensure efficient design.

I remember you mentioned simulations. How do air bubbles help in visualizing these flows?

Air bubbles can be injected into the flow, creating visible paths of streamlines, which illustrate how the fluid moves around obstacles.

What about the rotating cylinders we discussed earlier?

Exactly! The rotation creates complex flows that can also be analyzed using stream functions, helping in designing better industrial systems.

Is there a way to visualize the effects of acceleration or deceleration in these flows?

Yes, streamlines will cluster together or spread apart to indicate those changes. Closer lines represent higher velocities, while further apart indicates slower flow.

In summary, stream functions are invaluable tools in both theoretical and applied fluid mechanics.
Deriving Velocity from Stream Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

We’ve discussed the theory; now let's practice deriving velocity components from a stream function.

What if the stream function was something simple, like ψ = xy?

In that case, remember our formulas: `u = ∂ψ/∂y` and `v = - ∂ψ/∂x`. Can you compute `u` and `v`?

So `u = x` and `v = -y`. Got it!

And how does this relate to flow direction?

The values tell us how fluid moves relative to the coordinate system, giving a clear picture of direction and speed.

Would this change if we were looking at compressible flow?

Yes, for compressible flows, the stream function would need to factor in density, thus changing how we derive velocity.

To summarize, deriving velocity from stream functions involves straightforward differentiation, which helps us assess flow characteristics effectively.
Exploring Continuity and Mass Conservation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’ll explore the relationship between stream functions and mass conservation principles.

Why is mass conservation important in fluid mechanics?

Mass conservation ensures that mass is neither created nor destroyed as it moves through a flow field. Stream functions aid in visualizing this.

How do we prove that the stream function satisfies mass conservation?

We derive the continuity equation and find that using stream functions ensures the velocity divergence is zero, confirming mass is conserved.

So any time we see stream functions, we should think of conservation of mass?

Absolutely! It’s a fundamental principle in deriving the equations governing fluid flow.

Can we always use stream functions, or are there limitations?

Stream functions are most effective in incompressible flows or certain ideal conditions. For more complex flows, we may require other analyses.

In summary, stream functions provide a powerful tool in understanding mass conservation in fluid dynamics.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the role of stream functions in fluid mechanics, emphasizing their significance in visualizing and analyzing fluid flow, especially in cylindrical coordinates. The section also covers the derivation and implications of stream functions in relation to velocity fields and mass conservation equations.
Detailed
Detailed Summary of Cylindrical Coordinate Systems
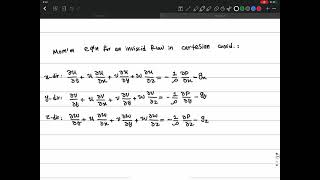
In fluid mechanics, stream functions are essential for simplifying the analysis of flow fields, particularly in cylindrical coordinate systems. This section begins by introducing the fundamental concept of stream functions, illustrating how they relate to velocity fields in two-dimensional flows.
We learn that the stream function is a scalar function from which velocity components can be derived. Specifically, the velocity components in cylindrical coordinates can be expressed in terms of the gradient of the stream function:
- The velocity in the radial direction (u) is equal to the partial derivative of the stream function with respect to the angular coordinate (theta).
- The velocity in the angular direction (v) is the negative partial derivative of the stream function with respect to the radial coordinate (r).
Key properties of stream functions are also discussed, such as their ability to satisfy continuity equations, thereby ensuring mass conservation during fluid flow. The section includes practical examples, such as visualizing complex flows around rotating cylinders and F-16 fighter jets using computational fluid dynamics (CFD).
Further, we extend our analysis to compressible and incompressible flows, detailing how stream functions can adapt to different flow conditions by incorporating parameters like fluid density. As we delve deeper, the use of stream functions aids in identifying aspects like acceleration and deceleration zones in fluid flows, represented visually through streamline patterns.
The significance of understanding stream functions in today's CFD landscape is emphasized, highlighting the intersection of classical fluid mechanics principles with modern computational techniques.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Stream Functions
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let us go very basic of the streamline and stream functions which is essential for an undergraduate student. We will talk about what is the stream functions in a two-dimensional coordinate system.
Detailed Explanation
Stream functions are mathematical tools used in fluid mechanics to simplify the analysis of fluid flow, particularly in two-dimensional flow scenarios. A stream function represents the flow field where the flow lines, or streamlines, are derived from it. The concept is important because it reduces the complexity of addressing fluid motion in two dimensions, allowing students to focus on the essential aspects without getting overwhelmed by the details.
Examples & Analogies
Imagine you're watching a parade. Each float represents the flow of fluid, and the paths they take are the streamlines. Instead of tracking each float individually, you could think of the entire parade route as a single planned path. This is similar to how stream functions simplify fluid flow analysis by converting complex paths into easier, manageably calculated routes.
Velocity Components and Stream Functions
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We can see that the velocity components are defined based on the stream functions. The scalar velocity component in the x direction corresponds to the first gradient or partial derivative of the stream function with respect to y.
Detailed Explanation
The relationship between stream functions and fluid velocity components enables the calculation of velocity without explicitly resolving the equations of motion. For instance, if we define u as the velocity component in the x direction, it is found by taking the partial derivative of the stream function (ψ) with respect to y. Meanwhile, the velocity component v in the y direction can be defined as the negative partial derivative of the stream function with respect to x. This relationship allows fluid dynamics problems to be approached more simply and systematically.
Examples & Analogies
Think of the stream function like the map of a city. When you look at a map (stream function), you can determine how to move through the city (velocity components) without needing to understand the streets' intricate details. If you know where you want to go (the flow direction), you can easily find the route based on the map.
Applications of Stream Functions
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Stream functions are crucial not only in theoretical analysis but also in practical applications, including Computational Fluid Dynamics (CFD).
Detailed Explanation
In modern fluid mechanics, particularly with the use of Computational Fluid Dynamics (CFD), stream functions help visualize and analyze complex flows. CFD simulations assist engineers in predicting fluid behavior in various contexts, such as around aircraft (like the F-16) or within pipeline systems. Understanding how to derive and apply stream functions permits engineers to resolve issues effectively, considering both practical effectiveness and computational efficiency.
Examples & Analogies
Consider a sophisticated video game where players can visualize the movements of water and air around obstacles. Just like how these games utilize physics engines to simulate real-world fluid dynamics accurately, engineers use CFD to analyze and predict fluid behaviors using stream functions, thus helping design more efficient aircraft or pipelines.
Continuity Equations and Stream Functions
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Stream functions adhere to continuity equations, and their properties can indicate when mass is conserved, particularly in incompressible flow scenarios.
Detailed Explanation
The continuity equation in fluid mechanics states that the mass flow rate must remain consistent over a closed system. Stream functions help in satisfying this condition when defining fluid motion. For incompressible flow, it implies that the divergence of the velocity field is zero. Stream functions facilitate the analysis of flow fields by ensuring these conditions are met, thereby simplifying the problem-solving process.
Examples & Analogies
Think of how a water hose works. If you have a hose and you pinch it, the flow rate remains the same; only the velocity increases. Just like your action maintains consistent flow, stream functions manage to keep mass flow rates consistent in fluid analysis through the equations, ensuring accurate results without needing complex calculations.
Practical Considerations in Stream Functions
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In cylindrical coordinate systems, we can adapt the use of stream functions to analyze fluid flows effectively, allowing us to resolve more complex problems.
Detailed Explanation
In cylindrical coordinates, the flow behavior around objects such as cylinders can be modeled with stream functions. This adaptation facilitates the analysis of rotational or axisymmetric flows, where the flow is consistent around a central axis. The mathematical representation of flow patterns using stream functions in this system makes it easier to evaluate the effects of fluid properties, such as viscosity and density, and helps predict behavior in practical applications.
Examples & Analogies
Imagine a merry-go-round at a playground. The way children move around the central pole represents how fluid flows around cylindrical objects. The stream function helps predict not just their speeds but also the effect of getting closer or further away from the center, just like how fluid dynamics changes around obstacles in real-world applications.
Key Concepts
-
Stream Function: A tool for visualizing streamlines and deriving velocity components.
-
Velocity Field: Indicates the directions and speeds at various points in flows.
-
Mass Conservation: Underpins the continuity equation, ensuring no mass loss in flow systems.
-
Continuity Equation: A mathematical representation of mass conservation in fluid mechanics.
-
Difference between Compressible and Incompressible Flow: Describes how density affects flow characteristics.
Examples & Applications
Visualizing airflow around the F-16 fighter jet with stream functions demonstrates complex fluid dynamics.
Inserting air bubbles in simulations shows unsteady stream patterns around rotating cylinders.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Stream functions show the flow's dance; velocities shift with every chance.
Stories
Imagine a river (stream function) winding through valleys (streamlines), guiding fish (fluid particles) in a graceful dance without ever colliding.
Memory Tools
Remember 'Velocity = Gradients of Stream Functions’ to keep u and v derived from ψ clear.
Acronyms
CARE - Continuity, Acceleration, Radial, and Energy conservation in fluid dynamics.
Flash Cards
Glossary
- Stream Function
A scalar function whose contours represent the flow streamlines in a fluid field.
- Velocity Field
A vector field that represents the velocity of fluid particles at different points in space.
- Mass Conservation
A principle stating that mass cannot be created or destroyed in a closed system.
- Compressible Flow
A type of flow in which the fluid density changes significantly in response to pressure or temperature changes.
- Incompressible Flow
A type of flow in which fluid density is considered constant, especially for liquids.
- Continuity Equation
An equation that expresses the conservation of mass in fluid flow.
Reference links
Supplementary resources to enhance your learning experience.
