Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stream Functions
Unlock Audio Lesson
Today, we're going to start with an essential concept in fluid mechanics—the stream function. Can anyone tell me what they think a stream function is?
Is it related to how fluids move, maybe in terms of flow patterns?
Exactly! Stream functions help us visualize the flow of fluids by depicting streamlines—imaginary lines that represent the path that a small particle of fluid would follow.
So, are these streamlines always the same distance apart?
Great question! In regions where the flow is uniform, the streamlines may be evenly spaced. However, when fluids accelerate or change directions, the spacing between streamlines can vary, which indicates changes in velocity.
How do stream functions help in calculations?
Stream functions reduce the complexity of the fluid flow equations by allowing us to work with a single dependent variable instead of multiple velocity components. This simplification is particularly useful in two-dimensional flows.
That sounds really helpful! So they could make solving fluid dynamics problems easier?
Absolutely! By using stream functions, we can derive important relationships between velocity and the geometry of the flow, which leads us to simpler solutions.
To remember this concept, think of 'Stream Functions Simplifying Fluid Flow'—SFSFF. It encapsulates the primary role of stream functions!
Visualizing Flow with Stream Functions
Unlock Audio Lesson
Moving to visualizations, who has heard of Computational Fluid Dynamics, or CFD?
Isn’t that the software used to simulate fluid flow?
Correct! CFD tools like ANSYS Fluent allow us to create visuals of fluid flow that incorporate streamlines. For example, in our class project simulating the F-16 fighter jet, we applied stream functions to analyze airflow around the jet.
Did you say the velocities ranged from 0 to 550 meters per second? That’s really fast!
Yes, and depending on the flow conditions, different zones exhibit varying pressures and velocities, showing the complexity of airflow around aircraft.
How do we interpret these variations?
The colors indicate different velocities; dark colors may represent slower flow areas while lighter colors indicate faster flows. Understanding these can help us design better aircraft.
So, the visual helps in understanding not just the flow, but also the forces at play?
Exactly! And visualizing streamlines helps pinpoint potential problems such as turbulence or flow separation.
Applications of Stream Functions
Unlock Audio Lesson
Let’s discuss how can we apply stream functions to solve real-world problems. Can anyone give an example?
Maybe something like flow around a building?
Correct! When analyzing flow around a building, we can draw streamlines to visualize how the structure affects airflow. By examining these, we can identify areas of high and low pressure.
Could stream functions also be used in mechanical systems like rotating cylinders?
Yes! In the case of two rotating cylinders, we can inject air bubbles into the flow to visualize streamlines dynamically, illustrating how the flow behaves under unsteady conditions.
And if I understand correctly, the more we understand these patterns, the better we can control the flow?
Exactly! By studying these patterns, we can develop better designs to manage flow effectively, whether in buildings, aircraft, or even aquatic vehicles.
So the applications are wide-ranging, from improving aerodynamics to enhancing environmental designs?
Absolutely! Stream functions are invaluable to engineers across various disciplines.
Mathematical Derivations of Stream Functions
Unlock Audio Lesson
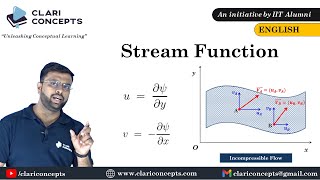
Now, let's talk about the mathematical aspect of stream functions. Who can define the relationship between stream functions and velocity components?
Is U the partial derivative of the stream function with respect to y?
Exactly! And V is the negative partial derivative of the stream function with respect to x. This is crucial for understanding how we derive the continuity equation.
So when we plug these into our equations, we simplify the calculations?
Correct! By substituting these relationships, we can often eliminate one variable and deal with a single function.
What about for compressible flows? Does it change?
Good question! For compressible flows, we incorporate density into the equations, but the foundational relationships remain similar.
I feel like having this algebra is essential in not only deriving equations but in practical application too!
Absolutely! Understanding the math behind these concepts is as important as applying them in real-world scenarios.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores the concept of stream functions, detailing their significance in simplifying fluid flow analysis within differential mechanics. It covers the application of stream functions in both incompressible and compressible flows, as well as in cylindrical coordinate systems. Numerous examples and visualizations, including CFD simulations of an F-16 fighter jet and rotating cylinders, illustrate the practical applications of stream functions in understanding complex fluid dynamics.
Detailed
In this lecture, Prof. Subashisa Dutta elaborates on stream functions, a fundamental tool in fluid mechanics used to analyze and visualize fluid flow. The lecture begins with an overview of streamlines and their representation in fluid flows, illustrated with examples from simulations using CFD software like ANSYS Fluent. Prof. Dutta explains how stream functions simplify the analysis of fluid motion by reducing the number of dependent variables in the equations governing fluid mechanics. This enables easier calculation of velocity and pressure distributions through streamlines.
The lecture covers both incompressible and compressible flow cases, emphasizing how stream functions can be defined and applied across various coordinate systems, including cylindrical coordinates. Students are introduced to the mathematical derivation of the stream function and its relationship to velocity components in 2D flows. The section concludes with examples and applications that highlight the importance of stream functions in practical scenarios, such as flow around buildings and complex aircraft shapes.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Good morning all of you for today class on stream functions as we have been discussing on differential analysis of fluid flow. Today we are going to discuss about the stream flow functions okay and which is as we discuss more details about virtual fluid balls...
Detailed Explanation
In this introduction, the professor sets the stage for the lecture on stream functions. Stream functions are mathematical tools that help describe fluid flow in a more manageable way. The mention of 'virtual fluid balls' suggests a visualization technique where streams of fluid are represented as spheres, aiding in understanding how fluid moves through different spaces.
Examples & Analogies
Imagine a river where the flow can be seen as small balls floating. Observing how these 'balls' interact with rocks or bends in the river helps us understand the flow patterns and even predict where the water might speed up or slow down.
Visualizing Streamlines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at the problems what we have solved as a undergraduate fluid mechanics lab conducted in the last years... These are the air bubble injections okay.
Detailed Explanation
The professor discusses practical applications of stream functions in simulations, specifically using CFD software like ANSYS. The visuals depict how streamlines form around objects in the flow, exemplified by an F-16 fighter jet. As the air bubble injections simulate fluid movement, students can observe the patterns of flow and velocity variations, illustrating complex interactions in a clear manner.
Examples & Analogies
Think about blowing bubbles in a pool; as the air escapes, you can see the trails that the bubbles make in the water. These trails are like streamlines, which help understand how water flows around your hand when you wave it through the water.
Basic Concepts of Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us go very basic of the streamline and stream functions which is essential for undergraduate students that part what I will cover it. So today I will be very basic way we will talk about what is the stream functions okay...
Detailed Explanation
This chunk tackles the foundational concepts of stream functions, emphasizing their significance in fluid mechanics. Stream functions allow fluid flow to be analyzed in two dimensions. The segment transitions into discussing compressible and incompressible flows and introduces cylindrical coordinate systems, making it clear that stream functions can be adapted for various coordinate frameworks.
Examples & Analogies
Consider how water flows through a garden hose. The size and shape of the nozzle can change the flow of water. Understanding stream functions is similar; they help illustrate how different factors (like the hose’s shape) affect fluid movement in two dimensions.
Mathematical Representation of Stream Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at that as I said it if the functions is a very simplified it is a 2 dimensional flow field as given this examples of this case you can have the mass conservation equations in terms of u and v...
Detailed Explanation
Here, the professor delves into the mathematical definitions of stream functions. By simplifying the variables into a single stream function, it becomes easier to express and solve the fluid flow equations. This approach reduces complexity, making calculations more straightforward in applications involving fluid mechanics.
Examples & Analogies
Think of organizing a messy room. Instead of dealing with multiple items scattered around, you gather everything into one box. This simplification allows for easier handling and understanding of the room's contents, much like how stream functions simplify fluid dynamics equations.
Stream Functions in Computational Fluid Dynamics (CFD)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Nowadays the tools like ANSYS fluent or any CFD softwares available to visual the fluid flow, how it is happening it. For example, like complex flow around a F-16 fighter jet...
Detailed Explanation
This section illustrates how modern technology applies the concept of stream functions in Computational Fluid Dynamics. By using software like ANSYS, students learn to visualize the flow patterns around complex shapes. These tools help in understanding the behavior of fluids under various conditions using numerical simulations.
Examples & Analogies
Imagine how architects use software to create 3D models of buildings. Just as the software helps them see how people will move through the space, CFD tools enable engineers to see how air or water moves around objects, aiding in design and analysis of aerodynamic features.
Interpreting Streamline Patterns
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I go for interpretations of the streamlines, okay. Like for examples, I have a corner. So as you know it, the streamlines will come like this, will come like this, come like this...
Detailed Explanation
This segment discusses how to interpret the patterns of streamlines visually. By understanding the spacing and direction of these lines, one can glean insights about the velocity and behavior of the flow. For instance, closely spaced lines indicate faster velocities while wider gaps suggest slower movement.
Examples & Analogies
Consider traffic on a highway. When cars are tightly packed together, they are moving quickly, whereas when there are fewer cars, the driving pace slows down. Similarly, the distance between streamlines reveals how fluid speeds change in various areas of flow.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stream Function: A benefit for simplifying calculations in fluid flow.
-
Visualization: How stream functions help visualize flow patterns.
-
Incompressible vs. Compressible Flow: Differences in analysis using stream functions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using stream functions to visualize airflow around a building and resulting pressure zones.
-
Simulating fluid flow around an F-16 fighter jet with visual patterns and velocities.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid flows, just take a glance, Stream functions show the dance!
📖 Fascinating Stories
-
Imagine a river flowing around a bend, its path marked by leaves and twigs—much like how streamlines define the flow of the water.
🧠 Other Memory Gems
-
Think of 'SFL' for Stream Functions Lead—an acronym to remind you that stream functions lead to easier analysis.
🎯 Super Acronyms
Remember 'SFF' for Stream Functions in Fluid Flow.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stream Function
Definition:
A mathematical function used in fluid dynamics to simplify the analysis of fluid flow by reducing the number of variables.
-
Term: Streamlines
Definition:
Lines that indicate the path that a small fluid particle will follow in steady flow.
-
Term: CFD (Computational Fluid Dynamics)
Definition:
A branch of fluid mechanics that uses numerical analysis and algorithms to solve and analyze problems involving fluid flows.
-
Term: Incompressible Flow
Definition:
Flow in which the fluid density remains constant; typically applies to liquids.
-
Term: Compressible Flow
Definition:
Flow where fluid density can change significantly, typically applies to gases.