Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Empirical Formula
Unlock Audio Lesson
Today, we are going to discuss the empirical formulation of Depth-Area-Duration relationships, specifically focusing on the equation P = P₀ e^{-kA}. Can anyone tell me what each of those variables represent?
P is the average depth of precipitation, right?
Exactly! And what about P₀?
P₀ is the maximum point rainfall at zero area.
Correct again! Now, what does the decay constant 'k' signify?
It shows how the depth decreases as the area increases?
That's right! A good way to remember it is that 'k' governs the rate of decrease. Let's summarize this: P indicates depth, P₀ maximum depth, 'k' is decay, and A is area.
Significance of DAD Relationships
Unlock Audio Lesson
Can anyone explain why DAD relationships are significant in hydrology?
They help us understand how rainfall is distributed over different areas!
Correct! DAD relationships provide insights for designing flood control systems. How do you think these equations help in flood estimation?
If we can estimate rainfall for various areas, we can predict how much water would contribute to flooding!
Exactly! This empirical approach maximizes our ability to prepare for weather events. Remember, understanding DAD relationships is crucial for effective flood management.
Empirical Formulations Varieties
Unlock Audio Lesson
Did you know there are alternative formulations of DAD relationships besides the exponential decay model?
Really? What kind of formulations?
Some use power-law or logarithmic relationships. These depend on the regional characteristics of rainfall data. Which do you think would be more applicable in mountainous regions?
Power-law might fit better due to the steep variations in rainfall!
That's a great deduction! Always consider the geographical and meteorological context when choosing forms.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses several empirical equations, particularly the commonly used equation P = P0e^(-kA), which relates the average precipitation depth over a specified area to maximum point rainfall. It highlights the significance of such formulations in understanding rainfall distribution across diverse regions.
Detailed
Detailed Summary
The empirical formulation of Depth-Area-Duration (DAD) relationships offers a crucial method in hydrologic analysis, particularly for estimating average rainfall over varying areas and durations. One widely used empirical equation is given as:
P = P₀ e^{-kA}
where:
- P: Average depth of precipitation over an area A.
- P₀: Maximum point rainfall (theoretical depth at zero area).
- k: Decay constant, which describes how quickly the depth decreases with area.
- A: Area (in km²).
This section emphasizes the role of these relationships in optimizing flood estimations and hydrological designs, stressing that alternate formulations may employ power-law or logarithmic equations based on the specific region and fitting of historical data. Such empirical methods are essential for deriving reliable DAD curves that facilitate effective flood management and resource planning.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Empirical Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Several empirical equations have been proposed to describe DAD relationships.
Detailed Explanation
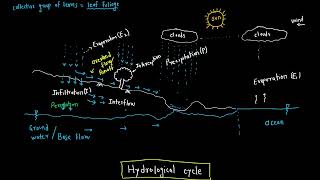
In the study of Depth-Area-Duration (DAD) relationships, researchers have developed various mathematical equations based on observational data. These empirical equations model how rainfall depth varies with area and duration, helping in predicting rainfall patterns under different conditions.
Examples & Analogies
Think of it like how you might estimate the time it takes to travel a certain distance based on your previous trips. Just as you might create averages from several journeys to estimate future travel times, scientists use data gathered from various rainfall events to formulate equations that predict rainfall behavior.
Key Equation for DAD Relationships
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
One widely used form is: P = P₀ e^{-kA}. Where: • P = Average depth of precipitation over area A, • P₀ = Maximum point rainfall (at zero area), • k = Decay constant, • A = Area (in km²).
Detailed Explanation
This equation expresses the average depth of precipitation (P) as a function of area (A). The maximum point rainfall (P₀) indicates the rainfall depth when the area is very small (the zero area scenario). The decay constant (k) represents how quickly precipitation depth declines as the area increases. As area increases, the average depth of rainfall diminishes, which this equation captures mathematically.
Examples & Analogies
Imagine a sponge soaking up water. The smaller the area of the sponge, the more water it can hold when dipped in a bucket. As you stretch the sponge out over a larger surface, it holds less water. The equation reflects this phenomenon, showing that as the area increases, the average amount of water (rain) decreases.
Alternate Formulations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Alternate formulations use power-law or logarithmic relationships, depending on region and data fit.
Detailed Explanation
In addition to the primary exponential equation, alternative formulations may also apply. These can include power-law or logarithmic equations which are chosen based on the nature of the data collected in a specific region. This flexibility allows researchers to create models that better fit the actual observed data, ensuring more accurate predictions.
Examples & Analogies
Think of it as tailoring a suit. Just as a suit can be designed in different styles to fit a person's unique body shape, these alternate formulations are like different suits, adjusted to best fit the specific characteristics of rainfall data in various regions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Depth-Area-Duration Relationships: A systematic method to estimate rainfall distribution.
-
Empirical Equation: Based on observed data, used widely in hydrology.
-
Decay Constant: Represents the reduction in depth with increased area.
-
Power-law Relationships: Alternative formulation based on regional data.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of using the empirical equation in practice is when estimating rainfall for flood control systems in urban planning.
-
A case study of mountainous regions might show a significantly different average rainfall using power-law relationships compared to flat landscapes.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For depth in the spot, P₀ hits the spot, while k shows what we got, how the rain's not a lot as area grows in thought.
📖 Fascinating Stories
-
Imagine a mountain where rain falls fiercely at the peak (P₀), but as it moves into the valley (area A), it gently fades away, all because the decay constant (k) regulates the spread.
🧠 Other Memory Gems
-
Remember ‘P-Point, k-Decay, A-Area’ when thinking of rainfall's interplay.
🎯 Super Acronyms
DAD for D=Depth, A=Area, D=Duration – a way to remember rainfall mapping!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: DepthAreaDuration (DAD) Relationships
Definition:
A systematic method to estimate average rainfall over varying areas and durations from point rainfall measurements.
-
Term: Empirical Equation
Definition:
A mathematical expression based on observed data rather than derived from theory.
-
Term: Decay Constant (k)
Definition:
A parameter that quantifies the rate of decrease in rainfall depth as area increases.
-
Term: Maximum Point Rainfall (P₀)
Definition:
The theoretical maximum depth of rainfall observed at a single point, typically at zero area.