Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Missing Rainfall Data
Unlock Audio Lesson
Today, we're going to discuss a very important topic: what happens when we have missing rainfall data. Can anyone tell me why we might experience missing values in rainfall records?
Maybe because of equipment failure?
Exactly! Equipment malfunction is a common reason. Other factors could include human errors or environmental disturbances. Let's explore how we can estimate these missing values.
Are there different methods to do that?
Yes, there are several methods. We'll cover three main techniques today.
Arithmetic Mean Method
Unlock Audio Lesson
Let's start with the Arithmetic Mean Method. This is the simplest way to estimate missing data. Can anyone explain how it works?
Is it just averaging the rainfall from nearby stations?
That's right! You take known rainfall values from surrounding stations and find their average. It works well when rainfall is uniform.
Does it always give accurate results?
Not always, especially in areas where rainfall varies significantly. Understanding when to use it is key.
Normal Ratio Method
Unlock Audio Lesson
Next, let's discuss the Normal Ratio Method. Who can tell me when we would use this method?
Is it when surrounding stations have different normal annual rainfalls?
Exactly! When there's a significant difference—more than 10%—the Normal Ratio Method helps adjust estimates based on normal rainfall.
How do we calculate it then?
Good question! We look at the normal rainfall of the missing station compared to nearby stations to adjust the estimates.
Inverse Distance Method
Unlock Audio Lesson
Finally, let’s tackle the Inverse Distance Method. Can anyone explain what this method entails?
It must involve calculating the distance between stations, right?
Yes! This method weights the rainfall values based on their distance—closer stations have more influence on the estimate. This provides a more localized estimate.
Would this method be better in urban areas?
It can be, especially in areas with variable rainfall patterns. Each method has its own applications depending on the context.
Summary of Methods
Unlock Audio Lesson
To wrap up, who can summarize the three methods we've discussed?
We learned about the Arithmetic Mean Method, the Normal Ratio Method, and the Inverse Distance Method!
Correct! Remember, choosing the right method depends on the conditions of the rainfall data and how uniform or varied it is. Great job today, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section presents several techniques for estimating missing rainfall data, including the Arithmetic Mean Method, Normal Ratio Method, and Inverse Distance Method. Each method varies in complexity and applicability depending on the characteristics of the surrounding rainfall data.
Detailed
Interpolation and Estimation of Missing Rainfall Data
In hydrology, accurate rainfall measurements are crucial, yet gaps in data can occur due to various reasons like equipment failure. To address these data gaps, several methods exist to estimate missing rainfall values.
- Arithmetic Mean Method: This is the simplest approach where the missing value is estimated as the average of the known rainfall values from surrounding stations. This method is effective in regions with relatively uniform rainfall distributions.
- Normal Ratio Method: This method is applied when there is significant variability (greater than 10%) in the normal annual rainfall across surrounding stations. It modifies the average of surrounding stations based on their normal rainfall compared to the missing station's normal value.
- Inverse Distance Method: This more advanced technique calculates weights for the surrounding known rainfall values based on the inverse square of their distance from the missing station. This means that closer stations contribute more to the estimate than those further away, leading to a more spatially aware estimation process.
Each of these methods is crucial for ensuring reliability and accuracy in rainfall data collection and analysis, which are fundamental in various applications including hydrological modeling and flood forecasting.
Youtube Videos
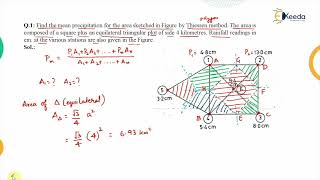
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Missing Data
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Rainfall records may have missing values due to equipment failure or recording errors. These can be estimated using the following methods:
Detailed Explanation
This chunk introduces the problem of missing rainfall data. Rainfall measurements can sometimes be incomplete due to malfunctioning equipment or errors in recording data. This means that not all rainfall events are logged accurately, which can lead to gaps in essential data for analysis. To address this issue, several methods are available for estimating these missing data points.
Examples & Analogies
Think of this like a student missing a few classes in school; if they want to catch up, they might ask friends for notes or look up the topics online. Similarly, in rainfall data, when measurements are missing, we use estimation methods to fill in the gaps.
Arithmetic Mean Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
7.5.1 Arithmetic Mean Method
P = (1/n) * Σ P_i
Where:
• P = missing rainfall value
• P_i = known rainfall values from surrounding stations
Simple and effective for regions with uniform rainfall.
Detailed Explanation
The Arithmetic Mean Method is one technique used for estimating missing rainfall values. Here, the missing value is calculated as the average of known rainfall values from nearby stations. This method works best in areas where the rainfall is relatively uniform, meaning the rainfall amounts don't vary much from one place to another. The formula shows that you take the sum of known values and divide it by the number of those values (n).
Examples & Analogies
Imagine gathering scores from a few friends who have taken the same exam and finding the average score to estimate how another friend might have performed, assuming they are similar students. Just as this gives a rough estimate of the missing score, the Arithmetic Mean Method estimates rainfall by averaging known measurements.
Normal Ratio Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
7.5.2 Normal Ratio Method
Used when the normal annual rainfall at surrounding stations differs significantly (by more than 10%).
P = (Σ (N_x * P_i))/(Σ N_i)
Where:
• N_x = normal rainfall at missing station
• N_i = normal rainfall at station i
• P_i = recorded rainfall at station i
Detailed Explanation
The Normal Ratio Method is used to estimate missing rainfall values when there is a substantial difference in normal annual rainfall between the surrounding stations, specifically more than 10%. The method adjusts for this difference by employing a ratio based on normal rainfall amounts (N_x for the missing station and N_i for the surrounding stations). This helps to ensure that the method accounts for the variability in expected rainfall between different locations.
Examples & Analogies
Consider food recipes that require different ingredient amounts based on the number of servings. If a recipe calls for 2 cups of flour for 4 servings, you would adjust the amount if you're only cooking for 2. Similarly, when rainfall measurements differ significantly, this method adjusts estimates to stay accurate based on surrounding data.
Inverse Distance Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
7.5.3 Inverse Distance Method
Weights the rainfall based on the inverse square of the distance between known stations and the one with missing data.
P = (Σ (P_i / d^2))/(Σ (1/d^2))
Where:
• d = distance from station i to the station with missing data.
Detailed Explanation
The Inverse Distance Method is a more sophisticated approach, where the influence of known rainfall data on estimating the missing value is based on their proximity. The formula uses the inverse square of the distance between each known station and the one with missing data. This means that closer stations have a greater weight in the calculation, as they are more likely to reflect similar rainfall patterns, while those further away contribute less to the estimate.
Examples & Analogies
Think of making a prediction about the weather based on information from nearby weather stations. If one station is very close, its data will likely be more relevant than data from a station far away. In this method, meeting the 'neighbors' who are geographically closer to you has more value in figuring out what the weather's been like.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Interpolation: The process of estimating missing values from available data.
-
Estimation of Missing Data: Techniques used to predict missing rainfall based on surrounding data sources.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a rain gauge reports 50 mm of rainfall and nearby gauges report 55 mm and 60 mm, the Arithmetic Mean Method estimates the missing data as (50 + 55 + 60) / 3 = 55 mm.
-
Using the Inverse Distance Method, if distance to gauge A is 2 km and gauge B is 5 km with recorded data 40 mm and 30 mm respectively, the estimated missing value would weigh the nearer gauge more heavily.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For missing data, don't fret or fume, just take the average with a little room!
📖 Fascinating Stories
-
Imagine a town where rain gauges sometimes break. The villagers use nearby gauges’ readings to guess how much rain fell, using averages, ratios, or distant values, to help them plan their farming!
🧠 Other Memory Gems
-
For missing rainfall, remember A, N, I: Average, Normal Ratio, Inverse Distance.
🎯 Super Acronyms
MRAID - Mean (Arithmetic), Ratio (Normal), And (Inverse) Distance (Methods).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Arithmetic Mean Method
Definition:
A technique for estimating missing rainfall values by averaging the results from surrounding stations.
-
Term: Normal Ratio Method
Definition:
A method for estimating missing rainfall based on the ratio of normal annual rainfall, applicable when surrounding stations significantly differ in rainfall.
-
Term: Inverse Distance Method
Definition:
An estimation technique that weights rainfall data from surrounding stations according to the inverse square of their distance to the missing station.