Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Direct Integration Method
Unlock Audio Lesson
Today, we are going to learn about the direct integration method for convolution. This method is applicable when our functions, f(t) and g(t), are piecewise continuous and manageable. Can anyone remind me of the convolution integral formula?
Is it the integral from 0 to t of f(τ) times g(t−τ)?
Exactly! We express it as: (f ∗ g)(t) = ∫0^t f(τ) g(t−τ) dτ. This allows us blending the two functions. Why do you think this method is important?
It helps in analyzing how one function influences another in the context of engineering!
Great point! Remember, convolution can model responses in systems such as structural load analysis and heat transfer.
Laplace Transforms Method
Unlock Audio Lesson
Now, let’s move to the second method: using Laplace transforms. Who can describe the first step?
You need to find the Laplace transforms of both functions, right? So F(s) = L{f(t)} and G(s) = L{g(t)}?
Correct! Then we multiply these transforms to find Y(s) = F(s) · G(s). Why do we do this instead of integrating directly?
Because multiplication in the Laplace domain is usually easier than calculating the convolution integral!
Yes! This method simplifies the analysis significantly, especially useful in signal processing. Always remember that the final step involves finding the inverse Laplace transform.
Relevant Applications
Unlock Audio Lesson
Let's talk about how we apply these techniques in real-life scenarios. Can anyone give an example of where convolution is used in engineering?
One example could be modeling how a structure responds to different loads over time!
Exactly! Another example could be in heat transfer analysis, where we determine how heat affects structures based on a heat input function. Both methods we discussed help solve such problems more effectively.
It sounds like convolution is a fundamental concept in analyzing systems.
Indeed! It is crucial for linear time-invariant systems and many branches of engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section focuses on two main methods for evaluating convolution integrals: direct integration, applicable to piecewise continuous functions, and utilizing Laplace transforms, which convert convolution into multiplication in the Laplace domain. Both techniques are vital for simplifying computations in signal processing and systems analysis.
Detailed
Evaluation Techniques for Convolution Integrals
The evaluation techniques for convolution integrals are essential in signal processing and systems analysis. In this section, we explore two primary methods:
Method 1: Direct Integration
This method is straightforward and applicable when the functions involved, denoted as f(t) and g(t), are piecewise continuous and manageable. The convolution integral is computed using the equation:
$$ (f ∗ g)(t) = \int_{0}^{t} f(\tau) g(t - \tau) d\tau $$
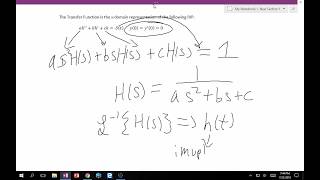
Method 2: Using Laplace Transforms
This method is particularly useful for transforming convolution calculations into simpler multiplication:
1. Compute the Laplace transforms: $$ L\{f(t)\} = F(s), L\{g(t)\} = G(s) $$
2. Multiply the transforms: $$ Y(s) = F(s) imes G(s) $$
3. Finally, obtain the inverse transform to find: $$ y(t) = L^{-1}\{ Y(s) \} $$
These techniques not only simplify the convolution process but also facilitate analysis in engineering applications, particularly in linear systems where convolution plays a critical role.
Youtube Videos
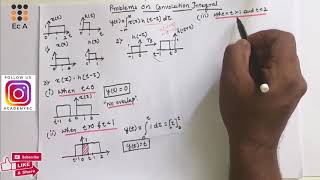
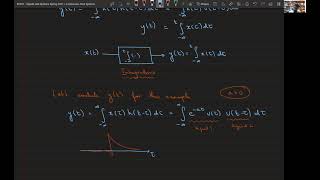
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Method 1: Direct Integration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applicable when both f(t) and g(t) are piecewise defined and manageable:
Z t
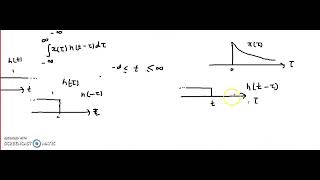
(f ∗g)(t)= f(τ)g(t−τ)dτ
0
Detailed Explanation
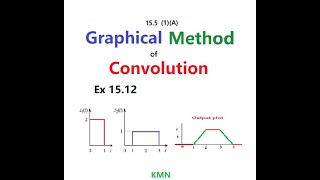
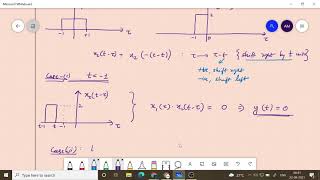
In direct integration for convolution, we compute the convolution of two functions f(t) and g(t) by integrating over a specified interval. The integral takes the form of the convolution integral:
\[ (f ∗ g)(t) = \int_{0}^{t} f(\tau) g(t - \tau) d\tau \]
This means we multiply the function f evaluated at a variable \( \tau \) by the function g evaluated at \( t - \tau \), and then integrate this product over all values of \( \tau \) from 0 to t. This method is straightforward but requires that both functions are manageable in terms of computation.
Examples & Analogies
Think of this like mixing two colors of paint. Imagine you're pouring a bit of blue paint (f(t)) into yellow paint (g(t)) as you go along, and you're mixing them together over a period of time to create a new shade. The direct integration is the process of carefully adding and blending these colors at every moment until you get your desired shade of green.
Method 2: Using Laplace Transforms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Step 1: L{f(t)}=F(s), L{g(t)}=G(s)
Step 2: Y(s)=F(s)·G(s)
Step 3: y(t)=L−1{Y(s)}
This approach simplifies many problems in signal processing and systems analysis.
Detailed Explanation
Using Laplace transforms to evaluate convolution integrals is a powerful technique, especially in engineering. Here’s how it works:
- Step 1: Compute the Laplace transforms of both functions, \( f(t) \) and \( g(t) \), resulting in \( F(s) \) and \( G(s) \).
- Step 2: The convolution of these functions in the Laplace domain is simply the product of their transforms: \( Y(s) = F(s) \cdot G(s) \).
- Step 3: Finally, we take the inverse Laplace transform of \( Y(s) \) to get back to the time domain function \( y(t) \).
This method is particularly useful for solving complex systems and equations, as it converts the difficult integral calculations into simpler algebraic multiplication.
Examples & Analogies
Imagine you are a chef who has to combine multiple ingredients for a recipe, and each ingredient represents a function. Instead of directly mixing each ingredient by taste (which could be complicated), you decide to write down each ingredient and its flavor notes as formulas (this is like taking the Laplace transform). Then, you can quickly mix the overall 'flavor' of your dish by simply combining the notes (multiplying the transforms), and finally adjusting the dish back in the kitchen to get taste just right (inverse transforming back to the original domain). This method makes complex cooking much simpler.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Direct Integration: A method for evaluating convolution integrals by directly calculating the integral of the product of functions.
-
Laplace Transforms: An alternative method that transforms functions into the Laplace domain for easier multiplication.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using direct integration to evaluate the convolution of f(t) = t and g(t) = e^(-t).
-
Applying the Laplace transform method to find the convolution through multiplication in frequency domain.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find what's combined, don't hesitate,
📖 Fascinating Stories
-
Imagine a river merging with a stream; each flow represents a different function. Their combined flow showcases how one influences the other over time, much like convolution combines two functions into a resultant response.
🧠 Other Memory Gems
-
C-LIM: Convolution - Laplace integration method. Remember C-LIM to recall the two main evaluation techniques.
🎯 Super Acronyms
D-LAMP
- For evaluating convolutions
- think Direct Integration
- then Laplace transforms
- Analyze
- Multiply
- and find the final result - D-LAMP!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Convolution
Definition:
A mathematical operation that blends two functions to produce a third function representing how one function influences another.
-
Term: Direct Integration
Definition:
A method of evaluating convolution integrals by directly integrating the product of the functions.
-
Term: Laplace Transform
Definition:
An integral transform that converts a function of time into a function of complex frequency, simplifying analysis.
-
Term: Piecewise Continuous Function
Definition:
A function that is continuous within certain intervals but may have breaks or discontinuities at certain points.