Change of Basis and Similarity of Matrices
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Change of Basis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're diving into the concept of 'Change of Basis.' Why is it important to represent linear transformations with different bases?

Maybe because it helps solve problems from different perspectives?

Exactly! Different bases can simplify complex problems. If we have a linear transformation T: V → V and two distinct bases B and B′, we use a change of basis matrix P to convert between them. Can anyone tell me what a basis is?

A basis is a set of vectors that can represent any vector in the space by linear combinations, right?

Correct! Think of it as a coordinate system for the space. The change of basis is a practical tool for interpreting data in various contexts.

How does this affect the calculations we do with linear transformations?

Good question! The mathematical representation changes, but the fundamental linear transformation remains the same. Keep in mind that these changes can reveal patterns or solutions not visible in one particular basis.

Can we use this change for simplifying engineering problems?

Absolutely! Engineers often use this method to model situations and simplify calculations, enhancing both analysis and design.

To summarize, changing the basis allows for easier handling of linear transformations and analyses in multiple reference frames.
Similarity of Matrices
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, switching to similarity of matrices. Who can tell me what it means for two matrices to be similar?

Is it that they represent the same transformation?

Exactly! Two matrices A and B are similar if we can find an invertible matrix P such that B = P⁻¹AP. Can anyone explain why this is significant?

Because similar matrices have the same invariants, like determinants and eigenvalues?

Right again! Maintaining these properties is crucial for understanding the behavior of a linear transformation. Who remembers what the terms 'determinant' and 'eigenvalue' mean?

Determinants measure volume scaling, and eigenvalues are scalars that indicate the factor by which eigenvectors are scaled?

Perfect! So even if the matrices appear different, they encode the same foundational structure and attributes of the transformation. This is especially useful in engineering applications, where different representations may clarify different aspects.

So by transforming matrices, we still get the same results in behavior, just in different forms?

Yes, that's spot on. To conclude, understanding matrix similarity is vital for simplifying and analyzing linear transformations effectively.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section explores how linear transformations can be represented in different bases, known as 'change of basis,' and describes matrix similarity, where two matrices represent the same transformation under different bases. Key properties such as determinants, traces, and eigenvalues are maintained in similar matrices.
Detailed
Change of Basis
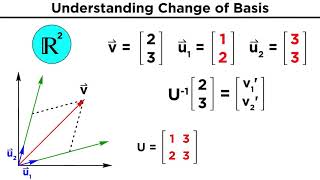
In linear algebra, understanding how linear transformations can vary depending on the basis used is essential. The change of basis technique allows us to represent a linear transformation in a different coordinate system or vector basis. If we have a linear transformation T: V → V, and two different bases B and B′ for the vector space V, a change of basis matrix P can transform coordinates from one basis to the other.
Similarity of Matrices
Similarity of matrices reaffirms that two matrices A and B are considered similar when there exists an invertible matrix P satisfying the relation B = P⁻¹AP. This concept is fundamental as it implies that similar matrices represent the same linear transformation under different bases. Notably, similar matrices share important characteristics: they have identical determinants, the same trace, characteristic polynomial, and eigenvalues. This means that various aspects of the linear transformation's behavior remain consistent, regardless of the basis employed for its representation.
In this section, we highlight the importance of changing bases in simplifying mathematical problems and positional interpretations across different reference frames.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Change of Basis
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Linear transformations can be represented differently depending on the basis used for the vector space. This concept is crucial in simplifying problems or interpreting data from different reference frames.
Detailed Explanation
In linear algebra, a change of basis refers to the process of expressing a linear transformation or vector in terms of a different set of basis vectors. Since different bases can provide different perspectives or simplifications, understanding how to switch between bases is essential for problem-solving. By using a different basis, we can often make data analysis more convenient or intuitive, especially when working with complex systems.
Examples & Analogies
Consider a situation where you are trying to navigate using a map. If you are looking at a city map, the streets and landmarks are oriented based on a specific grid or reference frame. Now, if you rotate the map to face a different direction, you are effectively 'changing the basis' of how you see the city. The same streets and landmarks are still there, but they are represented differently, making it easier to understand your navigation based on your current perspective.
Understanding the Change of Basis Matrix
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let T:V →V be a linear transformation and suppose B={v_1,…,v_n} and B′ ={v′_1,…,v′_n} are two different bases for V. Let P be the change of basis matrix from B to B′.
Detailed Explanation
The change of basis matrix, denoted as P, plays a crucial role in transforming vectors between different bases. If you have a vector expressed in basis B and you want to express it in basis B′, you multiply this vector by the matrix P. This matrix encodes how each vector in the old basis relates to the new basis. Understanding how to construct and use the change of basis matrix is vital in linear transformations and geometry, as it allows for a more intuitive analysis of systems across different perspectives.
Examples & Analogies
Think of learning a new language. Initially, you might think in your native language while learning to communicate in a new language. The change of basis here is like translating your thoughts into another language using a specific set of vocabulary and grammar rules (the change of basis matrix). Once you learn how to express your ideas in the new language, you can communicate more effectively and understand things from that cultural perspective.
Introduction to Similarity of Matrices
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This transformation of matrix representations under different bases is called similarity.
Detailed Explanation
Matrix similarity refers to the concept that two matrices A and B represent the same linear transformation when viewed from different bases. Specifically, two matrices are considered similar if there exists an invertible matrix P such that B = P⁻¹AP. This equality means that even though the matrices look different, they behave the same way in terms of linear transformations, showing that they share essential properties like eigenvalues and determinants.
Examples & Analogies
Imagine two different camera lenses that produce images of the same object from distinct angles. The objects may appear differently framed and accented, but they are capturing the same reality. The lenses represent the similarity aspect; they modify the perspective (the basis) without changing the fundamental nature of the subject (the linear transformation).
Properties of Similar Matrices
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Similar matrices represent the same linear transformation under different bases. They have: • The same determinant • The same trace • The same characteristic polynomial and eigenvalues
Detailed Explanation
Despite appearing different as matrices, similar matrices possess fundamental properties that remain invariant across changes of basis. The determinant provides information about the scaling factor of the transformation, the trace gives insight into the sum of eigenvalues, and the characteristic polynomial governs the eigenvalues' behavior. These shared properties allow for deep insights into the nature of linear transformations and their respective applications in various fields, such as physics and engineering.
Examples & Analogies
Think about owning two cars that perform identically, yet have different colors and interior designs. While their appearances differ, they function the same way regarding acceleration, handling, and fuel consumption. Just like the cars, similar matrices offer different visual representations but retain the same functional essence, enabling engineers and scientists to use them interchangeably while analyzing a system.
Key Concepts
-
Change of Basis: The process of converting a linear transformation to a different coordinate system.
-
Similarity of Matrices: Concept stating two matrices can represent the same linear transformation if they are related by an invertible matrix.
-
Determinants and Eigenvalues: Properties that remain invariant between similar matrices.
Examples & Applications
If a matrix A transforms vectors in standard coordinates, and we apply a change of basis using matrix P, the new matrix representation will be P⁻¹AP.
In engineering, changing the basis can help in simplifying the stress analysis of materials by transforming data into a more manageable format.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Change your basis, it’s quite neat, a new perspective can’t be beat.
Stories
Imagine a traveler who needs to navigate through various terrains. By choosing the right map, they can easily find their way—just like changing the basis helps us simplify complex linear transformations.
Memory Tools
For similarity, think of 'Denote, Trace, Eigen'; these three properties remain the same!
Acronyms
C.O.B.A.S.I.S. - Change Of Basis And Similarity In Space.
Flash Cards
Glossary
- Linear Transformation
A function from one vector space to another that preserves vector addition and scalar multiplication.
- Change of Basis
The process of converting the representation of a linear transformation to a different basis.
- Similarity of Matrices
A property where two matrices represent the same linear transformation under different bases, expressed as B = P⁻¹AP.
- Change of Basis Matrix
An invertible matrix that transforms coordinates from one basis to another.
- Determinant
A numerical value that summarizes certain properties of a matrix, such as scaling and invertibility.
- Eigenvalue
A scalar associated with a linear transformation that indicates how much an eigenvector is stretched or compressed.
- Trace
The sum of the diagonal elements of a matrix, invariant under similarity.
Reference links
Supplementary resources to enhance your learning experience.
