Composition of Linear Transformations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Transformation Composition
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to talk about the composition of linear transformations. Can anyone tell me what a linear transformation is?

Isn't it a function that preserves vector addition and scalar multiplication?

Exactly! Now, when we take two linear transformations, say T1 and T2, and combine them, we create a new linear transformation. This new transformation is referred to as the composition of T1 and T2.

How do we write that out?

Great question! We denote the composition as T2 ∘ T1. It means we first apply T1 and then T2 to our input. The formula is (T2 ∘ T1)(u) = T2(T1(u)).
Properties of Composition
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's explore some properties of composed transformations. First, can anyone guess if the composition of two linear transformations is also linear?

I think it should be linear, right?

Correct! The composition of two linear transformations is indeed another linear transformation. This means it preserves vector addition and scalar multiplication. Let's also look at how we can represent this in matrix form.

Do we use the matrices of T1 and T2 to do that?

Exactly! If T1 has matrix A and T2 has matrix B, then the matrix representation of the composition T2 ∘ T1 is given by BA. This tells us how the transformations interact through their matrices.
Application of Composition
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Last session, we covered the theoretical part of composition. Now, can someone provide a practical application for composing transformations?

Maybe in computer graphics, where transformations like scaling and rotation are applied in sequence?

That's a perfect example! In graphics, combining transformations allows for complex changes to images. Can anyone think of how we would represent that mathematically?

We would multiply the matrices representing each transformation!

Exactly! So, being able to compose transformations efficiently is crucial in many applications, including engineering.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore how two linear transformations can be combined to generate a new transformation. The composition retains the linear properties of the original transformations and can be represented using matrices, providing a systematic approach for analyzing their behavior.
Detailed
Composition of Linear Transformations
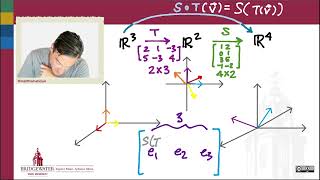
When we have two linear transformations, T1: U → V and T2: V → W, we can compose them to create a new linear transformation T2 ∘ T1: U → W. The composition, defined as (T2 ∘ T1)(u) = T2(T1(u)), preserves both linearity and structure.
Key Properties:
- The composition of two linear transformations results in another linear transformation.
- If T1 and T2 have matrices A and B, respectively, then the matrix representation of the composition is given by [T2 ∘ T1] = BA. This relationship highlights how manipulating matrices can model complex linear operations.
Youtube Videos




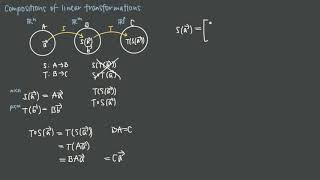




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Composition
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If T_1:U→V and T_2:V→W are linear transformations, then their composition T_2 ∘ T_1 :U→W is defined by:
(T_2 ∘ T_1)(u) = T_2(T_1(u))
Detailed Explanation
The composition of linear transformations is a way to combine two functions into one. In this case, we have two linear transformations: T_1, which takes vectors from space U and maps them to space V, and T_2, which takes vectors from V and maps them to W. The composition T_2 ∘ T_1 means that you first apply T_1 to a vector u from U, and then apply T_2 to the result of T_1. This combined process produces a new vector in space W.
Examples & Analogies
Imagine you are making a sandwich. The first step is to spread peanut butter on bread (T_1), and the second step is to add jelly on top of the peanut butter (T_2). You first complete the peanut butter step, and then you add jelly. The final sandwich is like the composition of two transformations in that it is the combined result of both individual actions.
Properties of Composition
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Properties:
- The composition of two linear transformations is also a linear transformation.
- If T_1 and T_2 have matrix representations A and B, respectively, then:
[T_2 ∘ T_1] = BA
Detailed Explanation
One important property of the composition of linear transformations is that the result will also be a linear transformation. This means the combination retains the characteristics of linearity, such as additivity and homogeneity. Furthermore, if T_1 and T_2 can be represented by matrices A and B, respectively, the matrix representation of the composition can be computed as the product of these matrices, specifically BA, not AB. This is because when you multiply matrices, the order matters - just like in our sandwich example, the order in which ingredients are added affects the final product.
Examples & Analogies
Consider the transformation of a raw ingredient into a finished dish. Think of making a cake: mixing the batter (A) and then baking it (B). The resulting cake is like the transformed output after the two operations. If you change the order and bake before mixing, you won't get a cake. Therefore, the order in which you perform linear transformations is critical to achieving the desired result.
Key Concepts
-
Composition: Combining two linear transformations into a new one.
-
Matrix Representation: How we express the transformations in matrix form to analyze their effects.
Examples & Applications
If T1 is a scaling transformation and T2 is a rotation transformation, then the composition T2 ∘ T1 scales a vector and then rotates it.
In computer graphics, composing multiple transformations is common, such as scaling followed by translating an object.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To compose is to merge, T1 and T2, watch them surge!
Stories
Imagine two friends who have different skills—T1 the scaler and T2 the translator. They work together; first, the scaler increases their height, then the translator shifts their position, combining their talents for greater effect.
Memory Tools
CATS: Composition As Two Steps (Apply T1 then T2).
Acronyms
COT
Compose
Operate
Transform.
Flash Cards
Glossary
- Linear Transformation
A function between two vector spaces that preserves the operations of vector addition and scalar multiplication.
- Composition
The process of applying one linear transformation after another, resulting in a new linear transformation.
- Matrix Representation
A way of expressing a linear transformation in terms of a matrix that acts on vectors.
Reference links
Supplementary resources to enhance your learning experience.
