Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Linear Transformations in ODEs
Unlock Audio Lesson
Today, we'll discuss how linear transformations connect with systems of differential equations. Have you heard about expressing ODEs in matrix form?
Not really. Can you explain how they relate?
Great question! We can express a system of first-order ODEs using linear transformations like this: dx/dt = Ax, where A is a matrix. This represents a transformation of the vector x.
So, is A just any matrix?
Excellent point! The matrix A must represent a linear transformation for the equations to be classified as linear. This ensures we can apply linear algebra techniques.
And what does the solution look like?
Exactly! The solutions are given by x(t) = e^(At)x(0). Here, e^(At) represents the matrix exponential, which helps us find the state of the system at any time t.
How do we compute e^(At)?
We can compute it via diagonalization or Jordan forms. Remember, understanding this process is key in solving applied problems in engineering.
To recap, we learned how ODEs can be expressed as linear transformations, and the solution uses the matrix exponential. Excellent participation today!
Applications in Civil Engineering
Unlock Audio Lesson
Now, let's explore some real-world applications of our earlier discussion on linear transformations in ODEs. Why is this important in civil engineering?
I think it has to do with modeling how structures behave under different loads?
Exactly! For instance, consider the vibration of a bridge. We can model the bridge's response using ODEs derived from linear transformations. What does that allow us to analyze?
The frequency of vibrations?
Right! This is known as modal analysis. By finding eigenvalues from our transformation, we can determine natural frequencies and how the structure behaves under various conditions.
How about the thermal conduction example you mentioned?
Great question! The heat equation can be modeled by linear transformations as well, effectively representing how heat diffuses. It uses similar methods as discussed for ODEs.
So, we rely on this understanding to predict how our structures will react?
Precisely! To sum up, we've seen the practical importance of linear transformations in solving ODEs for real-world civil engineering problems like vibrations and heat conduction.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Linear transformations are essential in expressing systems of ordinary differential equations (ODEs), as they can be represented in matrix form. Solutions to these ODEs using linear transformations are crucial in modeling real-world problems, such as vibrations in structures.
Detailed
In many physical systems, particularly in engineering, differential equations arise that can be represented using linear transformations. This section introduces how a system of ordinary differential equations (ODEs) can be expressed as a linear transformation using the form dx/dt = Ax, where A is a matrix representing the transformation. The solution is given as x(t) = e^(At)x(0), utilizing the matrix exponential which can be computed via diagonalization or Jordan forms. This framework is particularly useful in civil engineering applications, such as heat conduction, frame deflection in construction, and modal vibration analysis, allowing for the analysis and prediction of system behaviors.
Youtube Videos
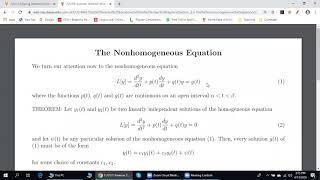
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Differential Equations and Linear Transformations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In many physical systems, especially in civil engineering (e.g., vibrations of a bridge, thermal conduction in a beam), systems of differential equations arise, which can be written using linear transformations.
Detailed Explanation
This chunk introduces the relationship between linear transformations and differential equations, particularly in fields like civil engineering. Differential equations often describe physical phenomena, such as how structures behave under loads or how heat flows through materials. By using linear transformations, we can represent these equations in a structured way using matrices, which simplifies analysis and computation.
Examples & Analogies
Imagine a bridge swaying gently in the wind. Engineers use differential equations to model this movement. By applying linear transformations, they can analyze how different parts of the bridge respond, just as a musician adjusts the notes of a song to create harmony.
System of Ordinary Differential Equations (ODEs)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
System of ODEs
dx/dt = Ax
Here, A is the matrix representing a linear transformation. The solution involves:
x(t) = e^(At)x(0)
Where e^(At) is the matrix exponential, which may be computed via diagonalization or Jordan forms.
Detailed Explanation
This chunk describes how a system of ordinary differential equations can be expressed in matrix form. The equation dx/dt = Ax shows how the rate of change of a vector x over time t relates to a linear transformation represented by the matrix A. The solution of this equation, x(t) = e^(At)x(0), indicates that we can find the state of the system at any time by applying the matrix exponential to the initial state x(0). This approach makes it easier to solve complex systems by transforming them into manageable matrix computations.
Examples & Analogies
Think of a roller coaster ride, where the position and speed of the coaster at any moment can be modeled using equations. Here, x(t) is like the coaster's position at time t, while e^(At) represents how the coaster moves through the track over time, influenced by gravity and design.
Practical Examples in Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Practical Examples
- Heat conduction modeled using Fourier’s law (linear diffusion operator)
- Frame deflection using beam bending equations (linear elasticity)
- Modal vibration analysis (linear system with eigen-decomposition)
Detailed Explanation
In this chunk, we see applications of linear transformations in real-world scenarios. Heat conduction can be modeled using Fourier's law, which describes how heat spreads through materials, mathematically treated as a linear diffusion operator. Frame deflection in structures like beams can be calculated using linear elasticity principles, which consider how materials deform under loads. Lastly, modal vibration analysis uses these mathematical tools to analyze the vibration characteristics of structures, helping engineers ensure stability and safety.
Examples & Analogies
Imagine baking a cake. The heat from the oven spreads throughout the cake batter (like heat conduction), causing it to bake evenly. Engineers use similar mathematical principles to ensure materials in buildings distribute stress and heat properly, much like ensuring every part of the cake gets the right amount of heat.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Linear Transformation: A mapping of vectors that preserves addition and scalar multiplication, crucial for expressing linear systems.
-
Ordinary Differential Equations: Mathematical equations that relate functions and their rates of change, significant for modeling physical systems.
-
Matrix Exponential: A necessary computation for solving systems of linear ODEs, providing solutions in engineering applications.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Heat conduction in beams can be modeled using a linear transformation to describe how heat diffuses over time.
-
Frame deflection in civil engineering structures can be analyzed through modal vibration analysis, leveraging linear transformations in ODEs.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
ODEs in matrix form, they take the norm, with e to the At, it helps us relate!
📖 Fascinating Stories
-
Imagine a bridge that sways, its vibrations measured in different ways through linear equations, safely predicting its sway.
🧠 Other Memory Gems
-
Remember: 'ODE - Open Differential Equation' to recall how we express these systems.
🎯 Super Acronyms
M.E.A.N. - Matrix Exponential for Analyzing Networks in ODEs.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Transformation
Definition:
A function mapping vectors from one vector space to another, preserving vector addition and scalar multiplication.
-
Term: Ordinary Differential Equations (ODEs)
Definition:
Equations involving functions and their derivatives, often used to describe physical systems.
-
Term: Matrix Exponential
Definition:
A function that takes a square matrix and returns another matrix, often used to solve systems of linear ODEs.
-
Term: Eigenvalues
Definition:
Scalars that indicate how much an eigenvector is stretched or compressed during a linear transformation.
-
Term: Modal Analysis
Definition:
An analysis method used to determine the vibration characteristics of a structure.