Rank and Nullity
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Rank
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's discuss the concept of rank. Rank refers to the dimension of the image of the linear transformation. Can anyone tell me why this is important?

Isn't the rank related to how many different outputs we can get from certain inputs?

Exactly! The rank indicates how many linearly independent vectors we can obtain. A higher rank means more information retention during transformation. Remember the acronym 'Rank = Reach' to help remember that rank measures the reach of our transformation.

What role does it play in solving linear equations?

Great question! The rank allows us to determine if a solution exists and if it's unique. Let's put that on hold momentarily to revisit it shortly.
Understanding Nullity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's turn our attention to nullity. Nullity is defined as the dimension of the kernel of the transformation. Who can explain what kernel means?

Isn't that the set of vectors that get transformed to zero?

Correct! The kernel essentially captures the 'missing' information, with nullity indicating how many directions collapse to zero. Remember, 'Nullity = Nothingness' to recall that it measures the degree of freedom lost. Let's move on to how nullity and rank interact.

How do they relate?

Great segue! The Rank-Nullity Theorem states that rank plus nullity equals the dimension of the original space. This tells us how those two concepts balance out in our linear transformation.
Rank-Nullity Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s dive into the Rank-Nullity Theorem. It states that the sum of the dimensions of the kernel and image equals the dimension of the original vector space. Anyone remember that equation?

Yes, it goes: dim(ker T) + dim(Im T) = dim(V)!

Exactly! This theorem is crucial in analyzing whether linear equations have solutions. What happens if the nullity is large?

That could mean many solutions or no unique solution, right?

Spot on! If the kernel dimension is greater, we risk having infinitely many solutions, which helps in understanding system behaviors.
Applications of Rank and Nullity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Lastly, let's connect rank and nullity to real-world applications. Soft engineering indicators use these concepts to assess structures. Can anyone think of where this might apply?

Maybe in analyzing forces in beams?

Absolutely! Understanding how forces distribute relates to rank and dimension collapse in structures. The more we grasp this, the better recommendations we can make during design.

So, mastering rank and nullity could improve our engineering effectiveness?

Precisely! Remember, the clearer we understand these dimensions, the better our designs and analyses will be!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section introduces the rank and nullity of linear transformations, highlighting their definitions, significance in linear algebra, and the Rank-Nullity Theorem, which connects the dimensions of the kernel and image of a transformation to the overall dimension of the vector space.
Detailed
Rank and Nullity in Linear Transformations
The concepts of rank and nullity are crucial for understanding the characteristics of linear transformations in linear algebra. For a linear transformation, denoted as T: R^n → R^m, rank is defined as the dimension of the image (or range) of T, while nullity refers to the dimension of the kernel (or null space) of T. The Rank-Nullity Theorem formalizes the relationship among these concepts by stating:
dim(ker T) + dim(Im T) = dim(V)
In terms of matrices, this can be expressed as:
nullity(A) + rank(A) = n
This theorem is vital for analyzing the solvability of linear systems and gives insights into how dimensions of different components of the transformation relate to one another. Understanding these properties can aid engineers and mathematicians in solving problems effectively and efficiently.
Youtube Videos



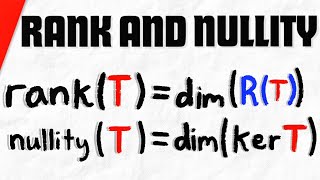





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Rank and Nullity
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
For a linear transformation T:Rn→Rm, the rank of T is the dimension of its image, and the nullity is the dimension of its kernel.
Detailed Explanation
In linear algebra, when we talk about a linear transformation T that maps vectors from one vector space (Rn) to another (Rm), two important concepts come into play: rank and nullity. The rank of T refers to how many dimensions are in the output space, or the image of T. Essentially, this tells us how many unique output vectors we can get when applying T to all possible input vectors. On the other hand, the nullity of T refers to the number of dimensions in the kernel (or null space) of T, which is the set of input vectors that get mapped to the zero vector in the output space. Together, these dimensions help us understand the behavior of the transformation.
Examples & Analogies
Think of a factory that produces cookies. The rank is like the number of different cookie types you can produce based on the ingredients and techniques you have. If you can make 5 types of cookies (like chocolate chip, oatmeal, peanut butter, etc.), then your rank is 5. The nullity, however, would represent the number of ingredient combinations you can input that result in no cookies (the failures, like mixing salt instead of sugar). If you have 2 combinations that lead to no cookies, then the nullity is 2.
The Rank-Nullity Theorem
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Rank-Nullity Theorem states: dim(kerT) + dim(ImT) = dim(V) Or in terms of matrices: nullity(A) + rank(A) = n.
Detailed Explanation
The Rank-Nullity Theorem is a fundamental theorem in linear algebra that relates the dimensions of the kernel and the image of a linear transformation to the dimension of the vector space from which the transformation originates. This theorem can be succinctly stated as: the dimension of the kernel (nullity) plus the dimension of the image (rank) equals the dimension of the domain vector space V. Mathematically, if we denote the dimension of the kernel as dim(kerT), the dimension of the image as dim(ImT), and the dimension of the vector space V as dim(V), the theorem summarizes it as dim(kerT) + dim(ImT) = dim(V). When working with matrices, this translates to: nullity(A) + rank(A) = n, where n is the number of columns in the matrix A.
Examples & Analogies
Imagine a classroom. The total number of students represents the total dimension of the classroom (dim(V)). The students who regularly attend class (the ones who show up and represent the image) reflect the rank of the classroom (dim(ImT)). Those who enroll but never attend (the absentees represented by the kernel) show the nullity (dim(kerT)). The Rank-Nullity Theorem tells you that if you add those who attend (rank) to those who don’t (nullity), you get the total number of enrolled students (dim(V)).
Importance of the Rank-Nullity Theorem
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This theorem is crucial for analyzing the solvability and behavior of linear systems.
Detailed Explanation
The Rank-Nullity Theorem is not just a theoretical concept; it has real implications in solving linear systems. When dealing with a system of linear equations, understanding the rank and nullity helps us determine whether the system has solutions and, if so, how many solutions exist. If the rank of the matrix of coefficients is equal to the number of variables, the system may have a unique solution; if the rank is less than the number of variables, there are infinitely many solutions or none at all, depending on the nullity. This relationship defines the structure and behavior of solutions to linear systems.
Examples & Analogies
Consider a treasure map where the landmarks represent equations in a system. If all clues (equations) point to a unique treasure location (solution), that's like having a full rank. If some clues lead to the same spot or a group of spots (infinitely many solutions), that’s akin to having a rank less than the number of clues. If the clues don’t lead anywhere (no solutions), it’s like having a nullity that leads to no treasures found.
Key Concepts
-
Rank: Measures the dimension of the image.
-
Nullity: Measures the dimension of the kernel.
-
Rank-Nullity Theorem: Relates the dimensions of the kernel, image, and total dimension.
Examples & Applications
For a linear transformation from R^3 to R^2, if the rank is 2, then the nullity is 1, since 2 (rank) + 1 (nullity) = 3 (dimension of R^3).
In an engineering context, analyzing a support beam, high rank indicates efficient use of materials by producing fewer unnecessary forces.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Rank is high, nullity's low, the more the inputs in, less the outputs flow.
Stories
Imagine a treasure map: the rank shows the bushes that lead to treasure, while nullity reveals the paths that lead to nowhere.
Memory Tools
Remember 'RANK' = Reach (dimension of image), and 'NULL' = Nothing (dimension of kernel).
Acronyms
RAN (Rank and Nullity) = Reach and Account for Nothingness.
Flash Cards
Glossary
- Rank
The dimension of the image of a linear transformation, indicating the number of linearly independent output vectors.
- Nullity
The dimension of the kernel of a linear transformation, indicating how many input vectors map to the zero vector.
- Kernel (Null Space)
The set of all vectors in a vector space that a linear transformation maps to the zero vector.
- Image (Range)
The set of all vectors in the codomain that can be produced by the transformation from vectors in the domain.
- RankNullity Theorem
A theorem stating that the dimension of the kernel and the dimension of the image of a linear transformation add up to the dimension of the domain.
Reference links
Supplementary resources to enhance your learning experience.
