Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Kernel
Unlock Audio Lesson
Let's start by discussing the kernel of a linear transformation. Can anyone tell me what the kernel represents?
Isn't it the set of all vectors that get mapped to zero?
Exactly! The kernel, denoted as ker(T), consists of all vectors v in the domain V such that T(v) equals the zero vector in W. It's a subspace of V. Why do you think knowing the kernel is important?
It helps us understand the solutions to linear equations, right?
That's correct! Understanding the kernel helps us analyze the nullity of the transformation. Remember the phrase 'zero is key,' which can help you recall that the kernel is all about what gets mapped to zero.
How do we find the kernel for a given transformation?
Great question! We typically solve the equation T(v) = 0 for all possible vectors v, finding the dimension of the solution space. Let's summarize: The kernel is pivotal in determining the structure of the transformation.
Exploring Image
Unlock Audio Lesson
Now, let's switch our focus to the image of a linear transformation. Who can explain what the image is?
It should be the set of all vectors that can be produced by mapping vectors from the domain, right?
Yes! The image, denoted as Im(T), is indeed the set of outputs that form subspace W. Just like we said with the kernel, knowing the image helps us understand the transformation—what outputs can we achieve?
So is it related to the concept of rank?
Absolutely! The dimension of the image is known as the rank of the transformation. A useful acronym here is 'RAVEN'—Rank is the dimension of the Image—helping you remember this relationship. Let's reflect: The image provides insights into the transformation's capabilities.
What happens if the image doesn't cover the entire codomain?
Good observation! This situation indicates the transformation is not onto. Summarizing: The image helps us communicate how effectively the transformation maps from V to W.
Relationship Between Kernel and Image
Unlock Audio Lesson
How do you think the kernel and image relate to each other within linear transformations?
They both help us understand the linear transformation's properties.
Exactly! The Rank-Nullity Theorem expresses this relationship: the dimension of the kernel plus the dimension of the image equals the dimension of the vector space V. Remember the catchphrase 'Kernel plus Image equals Space' for easy recall.
Can you relate it to real-life examples, like engineering applications?
Certainly! In engineering, the kernel reflects constraints or conditions to achieve stability, while the image indicates feasible states of a system. Summarizing, the Rank-Nullity Theorem encapsulates this important relationship between kernel and image, highlighting their significance.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the kernel (null space) and image (range) of a linear transformation, explaining that the kernel consists of vectors mapped to zero, while the image is formed by all the outputs of the transformation. Both concepts reveal the dimensions of the corresponding vector spaces and are foundational in understanding linear transformations.
Detailed
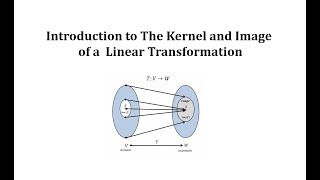
Kernel and Image of a Linear Transformation
In linear algebra, understanding linear transformations relies heavily on two fundamental concepts: the kernel and the image. The kernel (or null space) of a linear transformation, denoted as ker(T), includes all vectors in the domain that are mapped to the zero vector in the codomain. Formally, it can be defined as:
$$
ext{ker}(T) = \{ v \in V | T(v) = 0 \}
$$
This kernel is a subspace of the domain vector space, V. It plays a pivotal role in determining the solution sets of linear equations and also in characterizing the linear transformation's properties.
Conversely, the image (or range) of the linear transformation, denoted as Im(T), is the set of all vectors in the codomain that can be expressed as outputs of the transformation map. It can be represented as:
$$
ext{Im}(T) = \{ T(v) | v \in V \}
$$
This image is a subspace of the codomain W. Together, the kernel and image provide essential information about the behavior of linear transformations and are key components in studying aspects such as rank and nullity, as well as in applying the Rank-Nullity Theorem, which succinctly relates these dimensions. In summary, the kernel and image form the foundational backbone for understanding how linear transformations operate within vector spaces.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Kernel (Null Space)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The kernel of T, denoted by ker(T), is the set of all vectors in V that are mapped to the zero vector in W:
ker(T)={v∈V ∣T(v)=0}
It is a subspace of the domain V.
Detailed Explanation
The kernel of a linear transformation T, often referred to as the null space, is a crucial concept in linear algebra. It consists of all vectors v from the vector space V such that when transformed by T, they yield the zero vector in the codomain W. In mathematical terms, this is expressed as ker(T) = {v ∈ V | T(v) = 0}. The kernel is significant because it serves as a measure of how many vectors are collapsed to the zero vector when the transformation is applied. Since the kernel is formed from vectors in V, it is also a subspace of V, meaning it itself follows the principles of vector addition and scalar multiplication.
Examples & Analogies
Imagine you have a machine that transforms shapes, and some shapes, when passed through this machine, completely disappear, turning into nothing (the zero shape). The kernel of this transformation represents all the shapes that disappear, indicating that these shapes cannot be distinguished after the transformation is applied. This analogy helps visualize the concept of the kernel as all the inputs that lead to a complete 'loss' of form.
Image (Range)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The image or range of T, denoted by Im(T), is the set of all vectors in W that are images of vectors in V:
Im(T)={T(v)∣v∈V}
It is a subspace of the codomain W.
Detailed Explanation
The image, or range, of a linear transformation T is the collection of all possible outputs (or resulting vectors) when vectors from the domain V are applied to T. This is represented mathematically as Im(T) = {T(v) | v ∈ V}. The importance of the image lies in its ability to provide insights into the behavior of the transformation: it shows us what outputs are attainable from the inputs in V. Like the kernel, the image is also a subspace, which implies it contains the zero vector, is closed under addition, and closed under scalar multiplication.
Examples & Analogies
Consider a vending machine that offers various drinks. The image of this machine represents all the drinks that can be obtained, based on the options available inside it. If the machine takes in coins (input) and dispenses drinks (output), the image showcases all the drinks (outputs) for the different coins (inputs) you put in. Therefore, just as a vending machine limits what drinks can be dispensed, the image of a transformation limits what can be produced from the input vectors.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Kernel: The set of input vectors that are transformed to the zero vector.
-
Image: The set of output vectors that can be produced from the input vectors of the transformation.
-
Null Space: Synonymous with the kernel; reflects the set of vectors equating to zero.
-
Rank: Dimension of the image of a linear transformation.
-
Nullity: Dimension of the kernel of a linear transformation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a linear transformation defined by T(x) = Ax where A is a matrix, the kernel can be found by solving Ax = 0 to find all x that map to the zero vector.
-
If T is a transformation such that T(v) results in a line in the codomain, then the image of T is this line.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find the kernel, look for zero, the input vector's hero!
📖 Fascinating Stories
-
Imagine a magic box; if you put in the right key (a vector), zero comes out. The keys that work are in the kernel.
🧠 Other Memory Gems
-
KReaT: Kernel and Rank, and Image that's great!
🎯 Super Acronyms
K - Kernel, I - Image, N - Nullity, R - Rank.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Kernel
Definition:
The kernel of a linear transformation is the set of all vectors in the domain that map to the zero vector in the codomain.
-
Term: Image
Definition:
The image (or range) of a linear transformation consists of all vectors in the codomain that are obtained by applying the transformation to vectors in the domain.
-
Term: Null Space
Definition:
Another term for the kernel, indicating its role in identifying solutions to the linear transformation equating to zero.
-
Term: Rank
Definition:
The rank of a linear transformation is the dimension of its image, indicating how many directions in the codomain can be reached.
-
Term: Nullity
Definition:
The nullity of a transformation is the dimension of its kernel, reflecting the number of solutions to the transformation equating to zero.