Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Transformation Matrix
Unlock Audio Lesson
Today, we're going to discuss how linear transformations can be represented using matrices. Can anyone tell me what a linear transformation is?
A linear transformation is a function that maps vectors from one vector space to another while preserving vector addition and scalar multiplication.
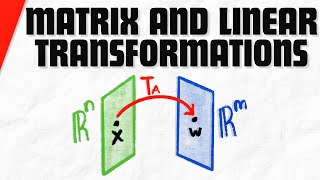
Exactly! Now, if we have a transformation T from R^n to R^m, let’s denote it as T: R^n → R^m. Do you know what it means for it to have a matrix representation?
Does it mean that we can use a matrix to perform the transformation on a vector?
Yes! There exists a unique matrix A such that T(x) = Ax for any vector x in R^n. This matrix A is called the standard matrix of the transformation.
So how do we get this matrix A?
Good question! A is constructed from the images of the standard basis vectors of R^n. Can anyone remind us what the standard basis vectors look like in R^n?
They are the unit vectors like (1, 0, 0...) for e₁, (0, 1, 0...) for e₂, and so on.
Exactly! The standard matrix A can be compiled by forming columns from T applied to each of the standard basis vectors: A = [T(e₁) T(e₂) ... T(eₙ)].
To recap, for a linear transformation from R^n to R^m, we can represent it with a matrix that captures how it acts on the standard basis vectors. This way, we can perform complex transformations using matrix multiplication.
Properties of the Standard Matrix
Unlock Audio Lesson
Now let’s focus on the implications of having a standard matrix for linear transformations. How might we use this in applications?
We can easily perform transformations on any vector by multiplying it with the matrix!
Correct! A major advantage is efficiency. For instance, in engineering, we often need to apply transformations to many vectors, and using a matrix allows us to use single multiplication instead of applying T individually.
Does the structure of matrix A change with different transformations?
Absolutely! Each linear transformation has its unique A matrix. For instance, in scaling transformations, the matrix might look different from those of rotation transformations.
Can we illustrate that with an example?
Definitely! A scaling transformation might be represented as A = λI, where λ is the scaling factor and I is the identity matrix, whereas a rotation transformation in two dimensions can have a matrix form like A = [[cosθ, -sinθ], [sinθ, cosθ]].
This highlights how matrices capture the essence of transformations effectively in computations.
Applications of Standard Matrix in Engineering
Unlock Audio Lesson
Now, let’s connect our understanding of standard matrices to civil engineering. How can these concepts be relevant in real-world scenarios?
I believe that in structural analysis, we can use matrices to determine how different forces will affect structures.
Exactly! For example, the transformation of forces and displacements in trusses can be simplified using the standard matrix form, allowing us to make predictions about structural stability.
What about finite element methods?
Great point! In FEM, we frequently transform local element matrices to a global coordinate system using matrix representations. This is fundamental in assembling the global stiffness matrix.
So the matrix is not just a theoretical tool but is actually used to bridge calculations to practical applications!
Yes! Remember, T(x) = Ax isn’t just a formula, but it's a vital tool engineers use in designing structures safely and efficiently. Always keep in mind the connection between theory and practice as you learn!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore that every linear transformation from R^n to R^m can be expressed uniquely as a matrix. This matrix, called the standard matrix, is constructed from the transformation of standard basis vectors, highlighting how these transformations can systematically manipulate vectors while preserving their linear properties.
Detailed
A linear transformation T:R^n → R^m is associated with a unique matrix A ∈ R^(m x n) such that for any vector x in R^n, T(x) = Ax. This matrix representation (called the standard matrix of the linear transformation) becomes clearer when considering standard basis vectors of R^n. Specifically, the standard matrix A can be formulated as A = [T(e₁) T(e₂) ... T(eₙ)], where eᵢ are the standard basis vectors of R^n. This section emphasizes the significance of matrix representations in understanding linear transformations and their applications, especially in engineering contexts.
Youtube Videos
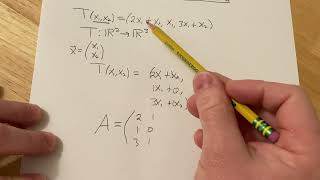
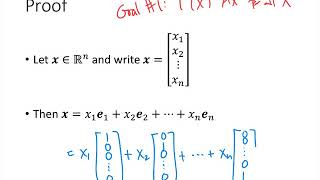
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of the Standard Matrix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If T:Rn→Rm is a linear transformation, then there exists a unique matrix A∈Rm×n such that:
T(x)=Ax,∀x∈Rn
Detailed Explanation
A linear transformation is a function that takes a vector from one space (Rn) and maps it to another space (Rm). The matrix A is what we use to perform this transformation. The equation T(x) = Ax shows that applying the transformation T to the vector x is equivalent to multiplying the vector x by the matrix A. This relationship is crucial because it connects linear transformations with matrix operations.
Examples & Analogies
Think of a linear transformation as a recipe for a dish. The matrix A serves as the list of ingredients and their quantities: just as following the recipe yields a certain dish (the output), applying the transformation using the matrix A gives you the transformed vector.
Unique Matrix Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This matrix is called the standard matrix of the linear transformation. If the basis of the domain and codomain is standard, then:
A=[T(e1) T(e2)…T(en)]
Detailed Explanation
The standard matrix is essentially a concise way to represent a linear transformation with respect to the standard basis vectors. The standard basis essentially provides a way to express any vector in a space. When we compute A using the transformations of these standard basis vectors (denoted as e1, e2, ..., en), we obtain a matrix that fully describes how the linear transformation T behaves with respect to the entire vector space.
Examples & Analogies
Imagine a company that uses a specific format to list all of its products. This format ensures consistency. Similarly, the standard matrix A helps us keep a consistent and clear representation of the linear transformation across different vectors, making it easier to understand how the transformation will operate in a systematic way.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Standard Matrix Representation: The unique matrix that represents a linear transformation.
-
Linear Transformation Properties: A mapping that preserves vector addition and scalar multiplication.
-
Images of Basis Vectors: The process of applying the transformation to standard basis vectors to construct the matrix.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a scaling transformation T(x) = λx, the standard matrix is A = λI.
-
For a rotation transformation T(x) in R², the standard matrix could be A = [[cosθ, -sinθ], [sinθ, cosθ]].
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find the matrix, just apply T, on basis vectors, just wait and see.
📖 Fascinating Stories
-
Imagine a wizard transforming a set of standard vectors into new forms by waving his wand; this wand is our matrix, representing the transformation magic!
🧠 Other Memory Gems
-
Remember 'MATRIX' for 'Mapping All Transformation Representations In eXtras.'
🎯 Super Acronyms
M.A.T. for Matrix A Transformation
- M: is for Method
- A: is for Apply
- T: is for Transform!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Transformation
Definition:
A function T:V →W that preserves vector addition and scalar multiplication.
-
Term: Standard Matrix
Definition:
The matrix representation A of a linear transformation that allows efficient computation of T(x) as Ax.
-
Term: Basis Vectors
Definition:
The set of vectors in a vector space that can be combined to represent any vector in that space.
-
Term: Vector Space
Definition:
A mathematical structure formed by a collection of vectors, which can be added together and multiplied by scalars.