Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Eigenvalues and Eigenvectors
Unlock Audio Lesson
Today, we're diving into eigenvalues and eigenvectors of linear transformations. Can anyone tell me what they think an eigenvector is?
Is it a vector that gets scaled by a transformation?
Exactly! An eigenvector keeps its direction when a transformation is applied. If T is a linear transformation, we say T(v) = λv for some scalar λ. What do we call λ here?
The eigenvalue?
Correct! How would we find these eigenvalues mathematically?
By solving the characteristic equation, right?
Yes! The characteristic equation is det(A − λI) = 0. Solving that gives us the eigenvalues. Great job!
To summarize: An eigenvalue is a scalar that indicates how much the eigenvector is scaled during the transformation.
Finding Eigenvalues and Eigenvectors
Unlock Audio Lesson
Let’s go through finding eigenvalues and eigenvectors with an example. Suppose we have a matrix A. Who remembers the first step?
We have to write the characteristic equation, right? Like det(A − λI) = 0?
Exactly! Once we compute that determinant, we can solve for λ. Then, how do we find the eigenvectors?
We substitute λ back into (A − λI)x = 0?
Correct! By solving this system, we find the eigenvectors associated with each eigenvalue. Let's try an example together next.
So remember: Eigenvalues are found from the characteristic equation, and eigenvectors are derived from solving the system using those eigenvalues.
Applications of Eigenvalues and Eigenvectors
Unlock Audio Lesson
Now, let’s discuss why learning about eigenvalues and eigenvectors is important. Who can give me an example of where we use these in engineering?
Like in modal analysis for vibrations?
Exactly! Eigenvalues represent natural frequencies. What might be a consequence of ignoring this in design?
If the structure resonates at those frequencies, it can fail?
Right again! This is why understanding eigenvalues is crucial for stability analysis and stress analysis as well. They guide engineers in design to ensure safety.
Remember, applying these concepts practically is just as important as the theory itself.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Eigenvalues and eigenvectors are key concepts in linear transformations that help identify how vectors are scaled and their directions remain unchanged. This section explains how to find eigenvalues using the characteristic equation and discusses their importance in civil engineering, particularly in areas like modal analysis and stability analysis.
Detailed
Eigenvalues and Eigenvectors of Linear Transformations
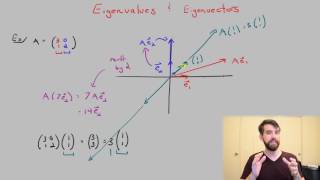
Eigenvalues and eigenvectors play a crucial role in the study of linear transformations, particularly in understanding scaling effects. Given a linear transformation T: V → V, an eigenvector is defined as a non-zero vector v ∈ V for which the transformation results in a scalar multiple of itself, expressed mathematically as T(v) = λv, where λ is referred to as the eigenvalue corresponding to the eigenvector v. This relationship indicates that eigenvectors maintain their direction even if their magnitude is scaled by the eigenvalue.
To find eigenvalues, one employs the characteristic equation, which is derived from the matrix representation A of the transformation T. The eigenvalues satisfy the equation: det(A − λI) = 0. The solutions to this equation yield the eigenvalues λ₁, λ₂, ..., λₙ. Subsequently, the corresponding eigenvectors can be determined by solving the linear system (A − λI)x = 0 for each eigenvalue.
The significance of these concepts in engineering extends to various applications, including:
- Modal Analysis: Eigenvalues represent the natural frequencies of vibration in structures, determining their response to dynamic loads.
- Principal Directions: In stress analysis, eigenvectors indicate principal stress directions, essential for design and failure analysis.
- Stability Analysis: The eigenvalues help assess the stability of equilibrium points in physical systems modeled by differential equations. Their real parts can indicate stability (negative real part) or instability (positive real part).
Thus, mastering eigenvalues and eigenvectors is fundamental for students and professionals working in fields requiring linear algebra applications, especially in engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Eigenvalues and Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
An important class of linear transformations are those that scale vectors instead of changing their direction.
Detailed Explanation
This chunk introduces the concept of eigenvalues and eigenvectors in linear transformations. It emphasizes that certain linear transformations scale vectors, meaning they change the length of the vector but preserve its direction. This property is significant because it helps identify how a transformation modifies vectors in a vector space without altering their orientation.
Examples & Analogies
Imagine a rubber band stretching. When you pull on it, its length increases (scaling) but it still points in the same direction. This is similar to how an eigenvector behaves under a linear transformation; it maintains its direction while its length changes.
Definition of Eigenvectors and Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Given a linear transformation T:V →V, a non-zero vector v∈V is called an eigenvector of T if: T(v)=λv for some scalar λ∈F, which is called the eigenvalue corresponding to v.
Detailed Explanation
In this chunk, we define what eigenvectors and eigenvalues are. An eigenvector, represented as 'v', is a vector that, when transformed by the linear transformation 'T', results in a new vector that is a scaled version of 'v'. The scalar 'λ' is the eigenvalue that quantifies this scaling. This relationship indicates that instead of changing direction, the transformation merely stretches or shrinks the vector.
Examples & Analogies
Consider a light beam traveling along a straight path. If you increase the brightness of the beam (analogous to scaling), it still travels in the same line (the direction). Here, the brightness change is like the eigenvalue, showing how much the intensity (length of the vector) changes while the direction of the beam (eigenvector) remains constant.
Finding Eigenvalues and Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let A be the matrix of the linear transformation T. The eigenvalues satisfy: det(A−λI)=0. This is called the characteristic equation. Solving it gives the eigenvalues λ1, λ2, …, λn. For each i, the eigenvectors are found by solving: (A−λiI)x=0.
Detailed Explanation
This chunk explains the method for determining eigenvalues and eigenvectors mathematically. To find eigenvalues, we utilize the characteristic equation derived from the determinant of the matrix 'A' minus 'λ' times the identity matrix 'I'. Setting this determinant to zero allows us to find the possible eigenvalues. Once we have the eigenvalues, we can substitute each one back into the equation (A−λI)x=0 to find the corresponding eigenvectors.
Examples & Analogies
Think of eigenvalues and eigenvectors like finding special angles and corresponding distances on a map. The characteristic equation is like determining which angles will get you the most straightforward paths (eigenvalues), and once you have those angles, you mark the exact positions (eigenvectors) on the map where you'd land.
Importance of Eigenvalues and Eigenvectors in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Eigenvalues and eigenvectors have various applications: 1. Modal Analysis: In structural dynamics, eigenvalues represent natural frequencies of vibration. 2. Principal Directions: In stress analysis, eigenvectors correspond to principal stress directions. 3. Stability Analysis: Eigenvalues indicate the stability of equilibrium in systems modeled by differential equations.
Detailed Explanation
In this chunk, we explore how eigenvalues and eigenvectors are utilized in civil engineering. Modal analysis uses eigenvalues to determine the natural frequencies at which structures vibrate, which is crucial for ensuring that buildings can withstand dynamic forces. Eigenvectors help identify principal stress directions, which are vital for understanding how materials will behave under loads. Furthermore, eigenvalues are key in stability analysis, providing insight into the equilibrium states of structures governed by differential equations.
Examples & Analogies
Imagine a bridge swaying in the wind. Engineers calculate the natural frequencies (eigenvalues) to ensure that the bridge doesn’t sway too much, avoiding disaster. The directions in which this swaying is most pronounced (eigenvectors) help them understand where to reinforce the structure for maximum stability and safety.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalue: The scalar that indicates how much an eigenvector is stretched or compressed during a transformation.
-
Eigenvector: A vector that remains in the same direction during the application of a linear transformation.
-
Characteristic Equation: A determinant-based equation that is solved to find eigenvalues.
-
Linear Transformation: A function that maps vectors while preserving addition and scalar multiplication.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a 2x2 matrix A represented a rotation, then any vector aligned with an eigenvector will keep its direction while potentially changing in magnitude based on the eigenvalue.
-
In structural analysis, the eigenvalues of a stiffness matrix can indicate the natural frequencies of vibration, influencing the design and safety measures of building structures.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvalues, eigenvectors, scaling all around - keeping the essence, without making a sound.
📖 Fascinating Stories
-
Imagine a traveler (the eigenvector) who carries a special badge (the eigenvalue) that tells him how much to stretch but never points him in a new direction.
🧠 Other Memory Gems
-
E.V.I. - Eigenvalues provide the scale, Vectors keep the trail, Independence in direction, that is their tale.
🎯 Super Acronyms
E.V.E.
- EigenValue = Eigenvector * Scalar.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalue
Definition:
A scalar λ such that T(v) = λv for some non-zero vector v, representing the scaling factor of the eigenvector.
-
Term: Eigenvector
Definition:
A non-zero vector v that remains in the same direction when a linear transformation is applied.
-
Term: Characteristic Equation
Definition:
The equation det(A − λI) = 0 used to find the eigenvalues of a matrix A.
-
Term: Linear Transformation
Definition:
A mapping T: V → W between two vector spaces that preserves vector addition and scalar multiplication.