Applications in Civil Engineering
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Non-Homogeneous Equations in Civil Engineering
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll explore how non-homogeneous differential equations apply to civil engineering. Can anyone tell me what makes these equations different from homogeneous ones?

Is it because they include external forces or inputs?

Exactly! Non-homogeneous equations describe how a system responds to both natural dynamics and external influences. This is crucial in areas like beam deflection and thermal processes.

What kind of external forces are we talking about?

Great question! Examples include loads on structures, heat sources in materials, or fluid forces like pressure. These factors can significantly affect system behavior.

Let's remember this with the acronym 'LEAF': Loads, External forces, Applications, and Forces. It highlights why we need to consider external inputs.
Applications in Beam Deflection
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

One major application is beam deflection. Does anyone remember the governing equation for beam deflection under load?

Is it the fourth derivative of displacement equal to the load?

Correct! The equation is d^4y / dx^4 = w(x). Here, w(x) represents the distributed load. Solving this tells us how much the beam will bend under that load.

How do we find the deflection from that equation?

By integrating the equation four times! You will capture all aspects of how the beam reacts to the applied load conditions. Remember, it's vital to understand boundary conditions to determine constants in the solution.

Can anyone visualize how this applies? Imagine a bridge under heavy traffic. The deflection calculations determine stability.
Thermal Conduction and Fluid Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let's look at thermal conduction. The equation is d^2T / dx^2 = -q(x)/k. Can someone explain what 'q(x)' represents?

It signifies a heat source, right?

Absolutely! This equation helps us determine how temperature changes within a medium when an internal heat source is present.

And what about fluid flow?

In fluid dynamics, we analyze flow impacted by external forces like gravity or pressure. Such scenarios often involve non-homogeneous equations too.

To summarise, understanding non-homogeneous equations is thus essential for predicting behaviors in physical systems, such as temperature variations and fluid motions.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section discusses the significance of non-homogeneous differential equations in civil engineering, particularly in modeling structural deflection under loads, thermal conduction with internal sources, and fluid flows influenced by external forces like pressure and gravity. Understanding these equations is crucial for accurate predictions and analyses in engineering contexts.
Detailed
Applications in Civil Engineering
In civil engineering, non-homogeneous differential equations play a vital role in accurately modeling and analyzing systems influenced by external forces or inputs. These equations arise in several scenarios, including:
- Beam Deflection under Load: The governing differential equation is expressed as d^4y / dx^4 = w(x), where w(x) represents the distributed load acting on the beam. Solving this equation helps engineers determine how the beam will deform under various loading conditions.
- Thermal Conduction with Sources: Another example includes the equation d^2T / dx^2 = -q(x)/k, where q(x) is a term representing heat sources in the medium. This equation assists in predicting temperature distributions in materials subject to internal heating.
- Fluid Flow Problems: Non-homogeneous equations also model fluid flow scenarios, where external forces such as pressure or gravity impact the flow regime.
Ability to solve these equations equips civil engineers with the skills needed to create safe and efficient designs for structures facing real-world challenges.
Youtube Videos





![Introduction to Engineering Hydrology and its Applications [Year - 3]](https://img.youtube.com/vi/Sds3dB-hA8E/mqdefault.jpg)



Audio Book
Dive deep into the subject with an immersive audiobook experience.
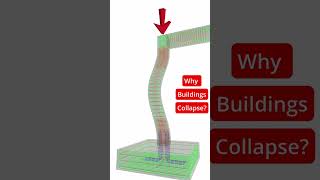
Beam Deflection Under Load
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Non-homogeneous equations are vital in:
• Beam deflection under load: Governing differential equation:
d4y
EI = w(x)
dx4
where w(x) is the distributed load (forcing function).
Detailed Explanation
In civil engineering, beam deflection under load is described using a fourth-order differential equation. The equation states that the fourth derivative of the deflection y with respect to x, multiplied by the flexural rigidity EI, equals the distributed load w(x). This represents how the beam bends under varying loads. The values of EI, which characterizes how much a beam resists bending, and the distributed load w(x) must be known to solve for y, the deflection.
Examples & Analogies
Think of a diving board. The board bends downwards when someone jumps off it. The board's flexural rigidity EI dictates how much it bends, while the weight of the diver acts as the load w(x). The equation helps engineers predict how much the board will bend to ensure that it remains safe for use.
Thermal Conduction with Sources
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Thermal conduction with sources:
d2T
= −
dx2 k
where q(x) is the heat source.
Detailed Explanation
This portion of the section discusses how non-homogeneous equations are used to model thermal conduction with internal heat sources. In the equation, T represents temperature, and the second derivative of T with respect to x equals negative one divided by the thermal conductivity k, indicating how temperature changes in a medium when heat is applied from an external source. Understanding this relationship is key for engineers designing systems involving heating, insulation, or cooling.
Examples & Analogies
Imagine a heated metal rod. When one end is placed near a flame, that end becomes hotter, and the heat travels along the rod. The temperature along different points of the rod as it heats up is described by this equation. Engineers can predict how quickly the heat will spread and ensure materials can handle the temperature changes.
Fluid Flow Problems
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Fluid flow problems where external forces like pressure or gravity act on the system.
Detailed Explanation
In this sub-topic, the role of non-homogeneous equations in fluid dynamics is introduced. When external forces such as gravity or pressure are applied, they affect how fluids move through different paths. The governing equations describe this interaction by indicating how changes in pressure or elevation alter fluid velocity or flow patterns, making it relevant in various engineering applications like water supply systems and drainage.
Examples & Analogies
Think about water flowing through a pipe that slopes downward. Gravity pulls the water down, affecting its flow speed. Engineers need to understand these changes to design pipes that transport water efficiently and safely. The equations help predict how much pressure is needed to keep the water flowing at the desired rate.
Importance for Civil Engineers
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Being able to solve non-homogeneous equations equips civil engineers to model and analyze these physical systems accurately.
Detailed Explanation
Solving non-homogeneous equations is crucial for civil engineers as it allows them to accurately predict how structures will respond to loads, temperature changes, and external forces. This capability is fundamental in ensuring the safety and stability of constructions like bridges, buildings, and roadway systems. Engineers use these predictions to make informed decisions during the design and construction processes.
Examples & Analogies
Imagine constructing a skyscraper. Before the first brick is laid, engineers must ensure the building can withstand wind, earthquakes, and other forces. By solving non-homogeneous equations, they can simulate and anticipate how the building will behave under various conditions, ensuring its safety and longevity.
Key Concepts
-
Non-Homogeneous Equations: Essential for modeling real-world civil engineering scenarios impacted by external forces.
-
Beam Deflection: Analyzing deflection helps ensure structural integrity under loads.
-
Thermal Conduction: Understanding heat transfer is crucial for temperature management in structures.
-
Fluid Flow: Control of external forces enhances fluid dynamics analysis.
Examples & Applications
A civil engineer uses non-homogeneous equations to assess how a bridge will deflect under heavy traffic loads.
Thermal modeling in buildings requires understanding of how heat sources impact temperature distributions.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To bend a beam from a load's decree, four times integrate is the key!
Stories
Imagine a bridge, heavy traffic flows, the deflection under load, the engineer knows! With equations in hand, they plot with care, ensuring safety—it's how they prepare.
Memory Tools
Remember 'BFT' for Beam, Fluid, and Temperature, the three areas impacted by non-homogeneous forces.
Acronyms
LEAF
Loads
External forces
Applications
Forces.
Flash Cards
Glossary
- NonHomogeneous Differential Equation
An equation that includes external forcing functions impacting a system's response.
- Beam Deflection
The displacement of a structural element under load.
- Distributed Load
The load distributed over a length of a beam rather than applied at a single point.
- Thermal Conduction
The process of heat transfer through a material due to a temperature gradient.
- Fluid Flow
The movement of fluid substances, impacted by forces like pressure or gravity.
Reference links
Supplementary resources to enhance your learning experience.
