Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Method of Undetermined Coefficients
Unlock Audio Lesson
Today we'll start with the Method of Undetermined Coefficients. This method is useful when our non-homogeneous term is a polynomial, exponential, or trigonometric function. Can anyone guess why it might be beneficial for these specific types?
Maybe because they have predictable derivatives?
Exactly! Their derivatives form predictable patterns, which allows us to guess the particular integral effectively. Let’s outline the steps for applying this method.
So, we start by making a guess for the form of the PI?
Correct! And then we substitute it into the differential equation to solve for the coefficients. If the guessed form appears in the complementary function, we modify it by multiplying by x or higher power. Does anyone remember the modification rule?
If our guess overlaps with the homogeneous solution, we just multiply by x to ensure linear independence?
That's right! Let’s go over a simple example together.
Example of Method of Undetermined Coefficients
Unlock Audio Lesson
Let's apply what we've learned. We have the non-homogeneous equation: -3y'' + 2y = e^x. What should our guessed form for the particular integral be?
Since it’s e^x, our guess could be something like A e^x?
Great start! However, because e^x is a part of the homogeneous solution, we should multiply by x, making our guess Ax e^x. Now what do we do next?
We need to differentiate it and substitute it back into the equation to find A?
Exactly! This process allows us to solve for A. Once we substitute, what should we do with A's value?
We add it to our complementary function to find the general solution.
Correct! Let’s summarize our findings from this example.
Method of Variation of Parameters
Unlock Audio Lesson
Now, let’s discuss the Method of Variation of Parameters, which is more versatile than our first method. Why do you think this method is needed?
Because not all forcing functions fit the standard types required for the first method?
Exactly! This method can work for a wider variety of non-homogeneous terms. Who remembers the general steps?
We first find the homogeneous solutions?
Right! And then we assume our PI is a linear combination of these homogeneous solutions multiplied by unknown functions. Does anyone know how we determine these functions?
By setting up a system of equations based on the original non-homogeneous equation?
Correct! And finally, we integrate those functions to get our particular integral. Let's practice this with an example next.
Example of Method of Variation of Parameters
Unlock Audio Lesson
For our example, we need to solve y'' + y = tan(x). What do we start with?
We first solve the homogeneous part to find y_h?
Correct! What did we find for the complementary function?
y_h = C_1 cos(x) + C_2 sin(x).
Great! Now we assume the particular integral has the form y_p = u_1(x) cos(x) + u_2(x) sin(x). What do we do next?
We set up our equations using the derivatives and the original non-homogeneous equation?
Exactly! After solving these equations, we can integrate u_1 and u_2 to find the PI. Let’s summarize the main points before we finish.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Finding the particular integral is crucial for solving non-homogeneous differential equations. The section introduces two primary methods used: the method of undetermined coefficients, applicable for specific functional forms, and the method of variation of parameters, which is broader in scope and applicable to various forms of non-homogeneous terms.
Detailed
Finding the Particular Integral
In solving non-homogeneous differential equations, determining the particular integral (PI) is a pivotal step toward achieving the general solution. This section outlines two principal methods of finding the PI: the Method of Undetermined Coefficients and the Method of Variation of Parameters.
Method of Undetermined Coefficients
This method is applicable when the non-homogeneous term, denoted as f(x), is a linear combination of polynomials, exponentials, trigonometric functions, or their products. The procedure involves:
1. Guessing a form for the PI based on the structure of f(x) with unknown coefficients.
2. Substituting this guess back into the original differential equation and solving for the coefficients through matching.
3. It is crucial to apply a modification rule if the guessed form appears in the homogeneous solution by multiplying it by x or higher powers for linear independence.
Example
Consider the equation:
\[ -3y'' + 2y = e^{x} \]
In this case, the guess for the PI would involve terms related to e^x.
Method of Variation of Parameters
This method broadens the application scope of finding the PI, suitable when f(x) does not adhere to the forms required by the previous method. The process involves:
1. Solving the corresponding homogeneous equation to find linearly independent solutions.
2. Assuming a solution format for the PI using these solutions weighted by unknown functions.
3. Setting up and solving a system of equations involving these functions and integrating to derive the PI.
Importance
Understanding these methods aids in modeling and producing accurate physical predictions in various engineering applications, showcasing the utility of non-homogeneous equations in real-world scenarios.
Youtube Videos
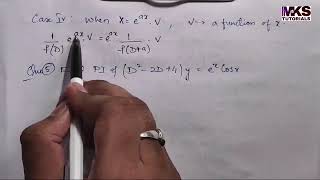
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Methods for Finding the Particular Integral
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
There are multiple methods for finding y (x). The most common ones used in engineering applications are:
Detailed Explanation
In engineering, when working with non-homogeneous differential equations, there are key methods to find the particular integral (PI). These methods allow for the solution of equations when external forces are applied to a system.
Examples & Analogies
Think of it like trying to heat a pot of water on a stove. The heat from the stove can be compared to the external forces acting on a system, and the way you monitor the water's temperature is similar to how engineers find the responses in differential equations.
Method of Undetermined Coefficients
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
6.3.1 Method of Undetermined Coefficients
When to Use
- Only when f(x) is a linear combination of functions like:
- Polynomials (e.g. x, x²)
- Exponentials (e.g. e^ax)
- Trigonometric functions (e.g. sinx, cosx)
- Their products (e.g. x e^x, e^x cosx, etc.)
Procedure
1. Guess a form for y (x), based on the form of f(x), with unknown coefficients.
2. Substitute this guess into the differential equation.
3. Determine the coefficients by matching both sides.
Important Note – Modification Rule
If the guessed form for y is a solution of the homogeneous part (i.e., appears in y_h), multiply by x or a higher power of x until linear independence is achieved.
Detailed Explanation
The Method of Undetermined Coefficients helps solve differential equations when the non-homogeneous function f(x) is in a specific format. First, you make an educated guess about the form of y_p that mirrors the structure of f(x). After guessing, you substitute this guess into the differential equation. Then, by matching coefficients on both sides of the equation, you can find the unknowns in your guess. If your guess is just like the solution from the homogeneous part, you modify it by multiplying it by x to ensure it’s unique.
Examples & Analogies
Imagine a student trying to solve a math problem by identifying the pattern in similar previous problems they solved. If they realize that part of their solution looks too familiar because it’s the same as a previous problem, they tweak their answer by adding an extra variable (like multiplying by x) to ensure it’s unique.
Example of the Method of Undetermined Coefficients
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example 1: Solve:
d²y/dx² - 3dy/dx + 2y = e^x
Solution:
- Auxiliary Equation: r² - 3r + 2 = 0 ⇒ r = 1, 2
- y_h = C₁e^x + C₂e²x
- Since e^x already appears in y_h, guess y_p = Ax e^x.
- Differentiate and substitute into the original equation.
- Find A, and then write the complete solution:
y = C₁e^x + C₂e²x + Ax e^x
Detailed Explanation
In this example, we start with a non-homogeneous equation where the right side is e^x. The first step is finding the homogeneous solution (y_h) using its auxiliary equation. Since e^x is already in the y_h, we use a new guess for the particular integral y_p, which is Ax e^x. By substituting this guess back into the original equation, we can solve for A and obtain the complete solution by adding y_h and y_p together.
Examples & Analogies
Consider tuning a musical instrument. You start with a basic sound but realize your original string is already in tune (the homogeneous solution), so you add another layer of sound (the Ax e^x) to enrich it. Once you match the new sound’s pitch with the existing notes, you have a harmonious tune (the complete solution).
Method of Variation of Parameters
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
6.3.2 Method of Variation of Parameters
When to Use
- When f(x) is not of the standard type or not suitable for undetermined coefficients.
- Works for any form of f(x), but involves integration.
Procedure
Given:
- ay′′ + by′ + cy = f(x)
1. Solve the homogeneous equation to find y₁(x), y₂(x), the two linearly independent solutions.
2. Assume:
yₚ(x) = u₁(x)y₁(x) + u₂(x)y₂(x)
3. Find u₁(x), u₂(x) by solving the system:
u₁y₁ + u₂y₂ = 0
u₁′y₁ + u₂′y₂ = f(x)/(a)
4. Integrate u₁(x), u₂(x) to get u₁', u₂', then substitute into yₚ(x).
Detailed Explanation
The Method of Variation of Parameters is applicable when the function f(x) does not fit into simple forms appropriate for the previous method. Instead of guessing a specific function form, this method assumes that the particular integral is a combination of the independent solutions of the homogeneous equation, modified by functions u₁ and u₂. The next step is solving a system of equations to obtain these u functions, which are then integrated to finalize the particular integral.
Examples & Analogies
This method is akin to customizing a recipe where the base recipe is known (the homogeneous solutions), and you want to add new ingredients (the particular integral) that suit your taste. Instead of just adding any ingredient, you need to ensure it complements the base recipe by solving for what works best while keeping the dish balanced and delicious.
Example of the Method of Variation of Parameters
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example
Solve: y′′ + y = tan(x)
Solution:
- Homogeneous solution: y_h = Ccos(x) + Csin(x)
- Let y₁ = cos(x), y₂ = sin(x)
Using variation of parameters:
- u₁(x)cos(x) + u₂(x)sin(x) = 0
- -u₁'(x)sin(x) + u₂'(x)cos(x) = tan(x)
- Solve these equations to find u₁, u₂, integrate, and get the particular integral yₚ.
Detailed Explanation
In this example, we are asked to solve a differential equation where the right side is tan(x). We begin by finding the homogeneous solution. Then using the Method of Variation of Parameters, we set up equations with u₁ and u₂. By solving these equations, we find u functions, which we integrate to obtain the specific solution needed to solve the full equation.
Examples & Analogies
Picture a tailor sewing a suit. They use a predefined pattern (the homogeneous solution) but need to adjust the fit with custom measurements (u₁ and u₂). Instead of using one size fits all, they ensure the suit fits perfectly based on the unique characteristics of the person wearing it. Once adjusted, the suit is ready for wear (the solution to the equation).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Non-homogeneous differential equations: Equations that include terms representing external forces.
-
Particular Integral (PI): A specific solution that addresses the non-homogeneous part of the differential equation.
-
Method of Undetermined Coefficients: A technique to find the PI by guessing, suited for specific function forms.
-
Method of Variation of Parameters: A broader technique that utilizes homogeneous solutions for a wider range of non-homogeneous terms.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example using the Method of Undetermined Coefficients to find the particular integral for the equation -3y'' + 2y = e^x.
-
Example demonstrating the Method of Variation of Parameters applied to the equation y'' + y = tan(x).
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To guess then check, will help inspect, the PI we need to protect.
📖 Fascinating Stories
-
Imagine you are a detective finding clues (the PI) hidden in the mystery of equations. Each clue (guess) must be verified (through substitution) until the full story (solution) unfolds.
🧠 Other Memory Gems
-
GESS: Guess, Evaluate, Substitute, Solve for coefficients to remember the method of undetermined coefficients.
🎯 Super Acronyms
PIV
- Particularly Important in Variation
- to remember that particular integrals involve varying the parameters.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Nonhomogeneous differential equation
Definition:
A differential equation that includes a non-zero forcing function.
-
Term: Particular Integral (PI)
Definition:
A specific solution to the non-homogeneous differential equation.
-
Term: Method of Undetermined Coefficients
Definition:
A method used to find the PI when f(x) is a linear combination of specific types of functions.
-
Term: Method of Variation of Parameters
Definition:
A method to find the PI applicable to any form of f(x).
-
Term: Complementary Function (CF)
Definition:
The general solution of the associated homogeneous equation.