Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Method of Undetermined Coefficients
Unlock Audio Lesson
Today, we'll explore the Method of Undetermined Coefficients. This method is specifically for solving non-homogeneous linear differential equations when the forcing function, f(x), is a linear combination of certain types of functions. Can anyone give me an example of such functions?
How about polynomials like x or x squared?
Or exponential functions like e raised to some power?
Exactly! We can use polynomials, exponentials, trigonometric functions, and their combinations. Now, can someone tell me what we do first in the procedure?
We guess a form for the particular solution, y_p!
That's correct! We will base our guess on the form of f(x). Remember, this is an integral part of solving using this method.
Procedure and Examples
Unlock Audio Lesson
Let's go over the three main steps again. First, we guess a form for y_p. What comes next after that?
We substitute that guess into the differential equation!
Exactly! And once we substitute it, what's the final step?
We match the coefficients of like terms on both sides.
Perfect! For example, in our equation, d²y/dx² - 3 dy/dx + 2y = e^x, since e^x is part of our homogeneous solution, what would we guess for y_p?
We should try Ax e^x.
Exactly! This aligns with our modification rule when our guess overlaps with the homogeneous solution.
Challenges with Overlapping Solutions
Unlock Audio Lesson
Now, it's vital to remember that if our guessed y_p is part of y_h, we need to adjust it. What does that mean practically?
We multiply by x or a higher power of x to ensure they’re linearly independent.
Exactly! This ensures our particular solution is valid. Can anyone give me an example of a situation where we should apply this modification?
When f(x) includes terms like e^x if it’s already in the homogeneous solution!
Yes! You’re all grasping this well. Remember, maintaining independence between these solutions is crucial in analysis.
Real World Applications
Unlock Audio Lesson
Finally, let's discuss how this method applies to real-world situations, especially in civil engineering. Why is it important to solve these equations?
It helps to predict how structures will react to loads!
And it can model things like beam deflections or heat transfer.
Correct. We need these solutions for accurate predictions in our designs. Observing how external forces affect systems is critical in ensuring safety and efficacy.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section details the Method of Undetermined Coefficients used to find particular integrals of linear non-homogeneous differential equations. It outlines when to apply the method, the procedure to follow, and emphasizes the importance of modifying the guessed form when it overlaps with the homogeneous solution. Practical examples illustrate its application in engineering contexts.
Detailed
Method of Undetermined Coefficients
The Method of Undetermined Coefficients is a powerful tool for solving linear non-homogeneous differential equations of the form:
a
d^2y/dx^2 + b dy/dx + c y = f(x)
where f(x) is a known function representing the forcing term. This method is only applicable when f(x) can be expressed as a linear combination of certain types of functions, specifically polynomials, exponentials, and trigonometric functions, as well as their products.
When to Use the Method:
Use the Method of Undetermined Coefficients when the non-homogeneous term, f(x), is a combination of:
- Polynomials (e.g., x, x²)
- Exponentials (e.g., e^(ax))
- Trigonometric functions (e.g., sin(x), cos(x))
- Their products (e.g., xe^(ax), e^(ax)cos(x))
Procedure for the Method:
- Guess a Form for y_p(x): Based on
f(x), propose a form for the particular integral including undetermined coefficients. - Substitute into the Equation: Plug your guess into the differential equation to evaluate.
- Match Coefficients: Solve for the undetermined coefficients by equating the coefficients of corresponding terms on both sides of the equation.
Important Note:
If the guessed form for y_p(x) is also a solution of the homogeneous part (y_h(x)), you must modify your guessed form. Multiply it by x or a higher power of x to maintain linear independence.
Example:
For the equation,
d²y/dx² - 3 y' + 2y = e^x,
y_h = C₁e^x + C₂e^(2x) (solving the homogeneous part)
Since e^x is part of y_h, we guess y_p = Ax e^x. The solution involves determining A, leading to the complete solution as:
y = C₁e^x + C₂e^(2x) + A x e^x.
This technique is crucial for civil engineers in modeling dynamic systems subject to forces or external influences, enabling them to predict the behavior of structures when subjected to varying loads.
Youtube Videos
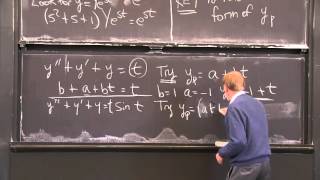
Audio Book
Dive deep into the subject with an immersive audiobook experience.
When to Use the Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When to Use
• Only when f(x) is a linear combination of functions like:
- Polynomials (e.g. x,x²)
- Exponentials (e.g. e^ax)
- Trigonometric functions (e.g. sin(x), cos(x))
- Their products (e.g. x * e^x, e^x * cos(x), etc.)
Detailed Explanation
The method of undetermined coefficients is applicable in specific scenarios. It is used when the non-homogeneous term f(x) is a linear combination of functions such as polynomials, exponentials, trig functions, or any products of these. This method is efficient in these cases due to the structured nature of these functions, allowing for straightforward guesses of the particular integral.
Examples & Analogies
Imagine you are trying to find a solution to a puzzle (the differential equation) and you notice that some pieces (types of functions) fit nicely together. Functions like polynomials or exponentials are like pieces designed to fit specific spots in this puzzle, making it easier to solve.
Procedure Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Procedure
1. Guess a form for y_p(x), based on the form of f(x), with unknown coefficients.
2. Substitute this guess into the differential equation.
3. Determine the coefficients by matching both sides.
Detailed Explanation
To apply this method, start by making an educated guess about the form of the particular solution, denoted as y_p(x). This guess should reflect the form of the known function f(x). Next, substitute your guessed solution into the original differential equation. The final step involves equating coefficients from both sides of the equation to solve for the unknowns in your guess.
Examples & Analogies
Picture a chef trying to recreate a famous dish they tasted. They might guess the ingredients (the form of y_p) based on what they remember. Then, by comparing their dish with the original (substituting into the equation), they adjust quantities (determine coefficients) until they are happy with the result.
Modification Rule
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Important Note – Modification Rule
If the guessed form for y_p is a solution of the homogeneous part (i.e., appears in y_h), multiply by x or a higher power of x until linear independence is achieved.
Detailed Explanation
There’s a key rule when using the method of undetermined coefficients: if your guess for y_p(x) happens to be part of the complementary function y_h(x), it will not work on its own. In such cases, you must modify your guess. This is commonly done by multiplying your initial guess by x or a higher power of x to ensure it is linearly independent from y_h(x). This adjustment allows for a correct determination of coefficients later on.
Examples & Analogies
Think of this situation like trying to fit an already existing piece in a puzzle. If the piece fits (matches the homogeneous solution), it won't help you solve the puzzle, so you need to modify it (multiply by x). It's like adjusting a shirt that's too small by adding layers or making it larger until it fits the unique spot.
Example Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Examples
Example 1: Solve:
d²y/dx² - 3 dy/dx + 2y = e^x
Solution:
• Auxiliary Equation: r² - 3r + 2 = 0 ⇒ r = 1, 2
• y_h = C₁ e^x + C₂ e²x
• Since e^x already appears in y_h, guess y_p = Ax e^x
• Differentiate and substitute into the original equation.
• Find A, and then write the complete solution:
y = C₁ e^x + C₂ e²x + Ax e^x
Detailed Explanation
Let's walk through the example. First, we find the auxiliary equation and solve it to get the roots, which gives us the complementary function (natural response). The term e^x already appears in y_h, so we modify our guess for y_p by multiplying it by x. After substituting the modified guess into the original differential equation, we find the coefficient A by matching terms on both sides of the equation. Finally, we combine y_h and y_p to form the total solution.
Examples & Analogies
Imagine you're fitting a new piece to a bridge that's already built (finding the complementary function). If one end of your new piece is too similar to an existing part, you can't attach it there and must reshape it (by multiplying by x). Once it fits, you can safely integrate it into the structure, just like solving our equation.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Method of Undetermined Coefficients: A technique for solving non-homogeneous linear differential equations using educated guesses for y_p.
-
Modification Rule: A guideline to alter the guessed y_p when it duplicates terms from y_h, ensuring linear independence.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For the equation d²y/dx² - 3 dy/dx + 2y = e^x, the complementary function is y_h = C₁e^x + C₂e^(2x). Thus, we guess y_p = Ax e^x to find the complete solution.
-
In the equation d²y/dx² + 4y = sin(x), our guess for y_p might be B sin(x) + C cos(x) since it fits the form.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Guess your y_p with care and flair, match the coefficients, be quite aware!
📖 Fascinating Stories
-
Imagine a builder who wants to know how his structure handles forces. He writes down the equation and puts his guess in play, making sure it's unique, so it leads the way!
🧠 Other Memory Gems
-
GSM: Guess, Substitute, Match coefficients - that's the key to solve using this method!
🎯 Super Acronyms
P.O.L.E
- Polynomial
- Other forms
- Linear combinations
- Exponential - the types of forms we can work with in this method.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Undetermined Coefficients
Definition:
A method used to find particular solutions to linear non-homogeneous differential equations by guessing a form based on the non-homogeneous term.
-
Term: NonHomogeneous Term
Definition:
The part of a differential equation that represents external forces or inputs, denoted as f(x).
-
Term: Particular Integral (PI)
Definition:
A specific solution to the non-homogeneous differential equation that is derived using the Method of Undetermined Coefficients.
-
Term: Complementary Function (CF)
Definition:
The general solution of the associated homogeneous equation in a differential equation.
-
Term: Linear Independence
Definition:
A condition where two functions do not overlap; ensuring they do not form a linear combination of each other.